VORGESCHICHTE
Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.
WAHR UND FALSCHE AUSSAGEN
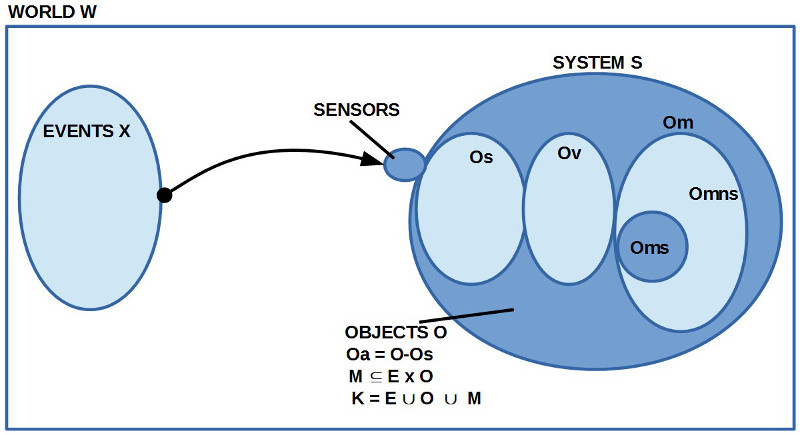
1. Nach dem Blogeintrag Avicenna 14b gibt es jetzt Ausdrücke A, B, …, die ‚wahr‘ oder ‚falsch‘ sein können und die wir deshalb ‚Aussagen‘ (auch ‚Propositionen‘) nennen. Aussagen können mittels aussagenlogischer Operatoren wie ‚NEGATION‘, ‚UND‘, ‚IMPLIKATION‘ usw. zu komplexeren Ausdrücken so verknüpft werden, dass jederzeit ermittelt werden kann, wie der Wahrheitswert des komplexen Ausdrucks lautet, wenn die Wahrheitswerte der Teilausdrücke bekannt sind. Ob im Einzelfall eine Aussage A ‚wahr‘ oder ‚falsch‘ ist, muss durch Rückgriff auf ihre Bedeutungsbeziehung M(A) geklärt werden. Bislang ist nur klar, dass die Bedeutungsbeziehung M nur allgemein eine Beziehung zu den (kognitiven) Objekten O herstellt (siehe Grafik oben).
2. Avicenna spricht aber nicht nur von Aussagen A allgemein, sondern unterscheidet die Teilausdrücke ‚Subjekt‘ S und ‚Prädikat‘ P, zusätzlich oft noch ‚Quantoren‘ Q.
FEINSTRUKTUR DER BEDEUTUNG VON AUSDRÜCKEN
3. Man kann und muss dann die Frage stellen, ob und wie sich auf der Bedeutungsseite die Unterscheidung in S und P auf der Ausdrucksseite widerspiegelt?
ECHTE UND UNECHTE OBJEKTE
4. In vorausgehenden Blogeinträgen zu Avicenna (Avicenna 4, 5, 7 und 11) wurde schon unterschieden zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte Objekte‘ sind solche Wissenstatbestände, die man zwar identifizieren und unterscheiden kann, die aber immer nur im Kontext von ‚echten Objekten‘ auftreten. ‚Unechte‘ Objekte werden meistens als ‚Eigenschaften‘ bezeichnet. Beispiel: die Farbe ‚Rot‘ können wir wahrnehmen und z.B. von der Farbe ‚Blau‘ unterscheiden, die Farbe ‚Rot‘ tritt aber nie alleine auf so wie z.B. Gegenstände (Tassen, Stühle, Früchte, Blumen, …) alleine auftreten.
5. Hier wird davon ausgegangen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf.
GATTUNG UND ART; KATEGORIEN
6. Ein Objekt kann viele Eigenschaften umfassen. Wenn es mehr als ein Objekt gibt – also O1, O2, … — die sowohl Eigenschaften Ex gemeinsam haben wie auch Eigenschaften Ey, die unterschiedlich sind, dann kann man sagen, dass alle Objekte, die die Eigenschaften Ex gemeinsam haben, eine ‚Gattung‘ (‚genus‘) bilden, und dass man anhand der ‚unterscheidenden Eigenschaften Ey‘ unterschiedliche ‚Arten‘ (’species‘) innerhalb der Gattung unterscheiden kann.
7. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden.
ONTOLOGISCHE UND DEFINITORISCHE (ANALYTISCHE) WAHRHEIT
8. Bislang ist der Wahrheitsbegriff $latex \top, \bot$ in dieser Diskussion an der hinreichenden Ähnlichkeit eines vorgestellten/ gedachten kognitiven) Objekts $latex a \in Oa$ mit sinnlichen wahrnehmbaren Eigenschaften $latex s \subseteq Os$ festgemacht worden. Ein ‚rein gedachtes Objekt $latex a \in Oa$ ist in diesem Sinne weder ‚wahr‘ $latex \top$ noch ‚falsch‘ $latex \bot$.
9. Setzt man allerdings eine Objekthierarchie O voraus, in der man von einem beliebigen individuellem Objekt a immer sagen kann, zu welchem Objekt Y es als seiner Gattung gehört, dann kann man eine Aussagen der Art bilden ‚a ist eine Tasse‘.
10. Wenn man zuvor in einer Definition vereinbart haben sollte, dass zum Begriff der ‚Tasse‘ wesentlich die Eigenschaften Ex gehören, und das Objekt a hätte die Eigenschaften $latex Ex \cup Ey$, dann würde man sagen, dass die Aussage ‚a ist eine Tasse‘ ‚wahr‘ ist, unabhängig davon, ob es zum kognitiven Objekt a ein ’sinnliches‘ ‚Pendant‘ geben würde oder nicht. Die Aussage ‚a ist eine Tasse‘ wäre dann ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr.
11. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a, die als solche nichts darüber sagt, ob es das Objekt a ‚tatsächlich‘ gibt, soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden, also einer Wahrheit, die sich auf das ‚real Seiende‘ in der umgebenden Welt W bezieht.
12. [Anmerkung: Dieses – auch im Alltagsdenken – unterstellte ‚Sein‘, die unterstellte übergreifende ‚Realität‘ ist nicht nur eine ‚Extrapolation‘ aufgrund sinnlicher Gegebenheiten ‚im‘ wissenden System, sondern ist in seiner unterstellten ‚Realität‘ auch nur eine sehr spezifische Form von Realität. Wie wir heute aufgrund immer komplexerer Messprozeduren wissen, gibt es ‚Realitäten‘, die weit jenseits aller sinnlichen Qualitäten liegen. Es fällt uns nur nicht so auf, weil diese gemessenen Eigenschaften X durch allerlei Prozeduren für unsere Sinnesorgane ‚umgerechnet‘, ‚transformiert‘ werden, so dass wir etwas ‚Sehen‘ oder ‚Hören‘, obgleich das gemessene X nicht zu sehen oder zu hören ist.]
13. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘).
14. Derjenige Ausdrucksteil As, der sich auf das echte Objekt a bezieht, ‚von dem‘ etwas ausgesagt werden soll (‚ist ein…‘, ‚hat …‘), dieser Ausdrucksteil wird als ‚Subjekt‘ S bezeichnet, und der Ausdrucksteil Ap, mittels dem etwas über das Subjekt ausgesagt wird, wird ‚Prädikat‘ P genannt.
15. Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.
16. [Anmerkung: Bei ’neuronalen Netzen‘ wäre das R-Objekt jenes Neuron, das die Verbindung zwischen zwei anderen Neuronen ‚realisiert‘.]
17. Fassen wir zusammen: Bei einem Ausdruck A der Art A=’Hans ist ein Mensch‘ gibt es den Ausdrucksteil As=’Hans‘ und den Ausdrucksteil Ap=’ist ein Mensch‘. Die Bedeutung des Ausdrucksteils As M(As) als M(‚Hans‘) ist ein Objekt h in der unterstellten Bedeutungshierarchie O des Sprechers, das gewisse Eigenschaften E(h) besitzt. Die Bedeutung des Ausdrucksteils Ap als M(Ap) bzw. M(‚ist ein Mensch‘) ist sowohl ein Objekt M mit Eigenschaften E(M) als auch eine Beziehung R_ist zwischen dem Objekt h und dem Objekt M, also R_ist(h,M). Die Beziehung ist definitorisch/ analytisch ‚wahr‘ wenn es gilt, dass die definierenden Eigenschaften E(M) des Objekts Mensch M auch bei den Eigenschaften E(h) von Hans zu finden sind, also $latex E(M) \subset E(h)$ .
BEZIEHUNGSRAUM – TRANSZENDENTALE BEDINGUNGEN
18.
Fortsetzung folgt
QUELLEN
- Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
- Digital Averroes Research Environment
- Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
- Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
- Stanford Encyclopedia of Philosophy, Aristotle’s Logic
- Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7
Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER