Archiv der Kategorie: Philosoph

Philosophie, Wissenschaft, Mystik. Eine Baustelle

Mystik, Philosoph, Wissenschaft

Journal: Philosophie Jetzt – Menschenbild
ISSN 2365-5062, 20. Dezember 2020 – 1.Januar 2021
URL: cognitiveagent.org, Email: info@cognitiveagent.org
Autor: Gerd Doeben-Henisch (gerd@doeben-henisch.de)

KONTEXT

(Letzte Änderung: 20.12.2020)

Die Themen Philosophie, Wissenschaft und Mystik kommen in diesem Blog sehr häufig vor; letztlich markieren sie die wesentlichen Koordinaten des Denkraums, der in diesem Blog aufgespannt wurde. Nicht so häufig, eher selten, sehr selten, kam es in der Vergangenheit zu direkten Verschränkungen aller drei Koordinaten. Zuletzt und am intensivsten vielleicht in dem Kongressbeitrag Kann Mystik rational sein? vom 26.Oktober 2019. Dass diese spezielle Themenverschränkung seit den Anfängen des Blogs im Dezember 2009 andauerte verweist einmal auf den Autor selbst, auf mich, andererseits aber auch auf Kontexte des Autors. In den letzten vier Jahren spielte hier eine besondere Lehrveranstaltung eine wichtige Rolle. Ihr Titel war Meditation als kulturelle Praxis. Angeregt durch den damaligen Präsidenten der Frankfurt University of Applied Sciences [FUAS] Frank Dievernich sowie dem Kanzler Reiner Frey durfte ich zusammen mit Ihnen ein Team bilden, um diese Lehrveranstaltung im Rahmen des Studium Generale im Sommersemester 2017 zu starten. Als langjährig Lehrender an der FUAS mit vielen interdisziplinären Lehrveranstaltungen konnte ich das Lehr-Konzept mit einbringen und durfte es dann im weiteren Verlauf bis zum Wintersemester 2020/1 einschlieslich begleiten. Aus Zeitgründen musste Frank Dievernich seinen Part zum Ende des SS2017 leider wieder abgeben. Glücklicherweise konnte wir im WS2017/18 Nicole Küchler-Stahn für das Modul gewinnen und ab SS2018 kam Julia Lademann zum Team. Zu diesem Zeitpunkt war dieses Modul das einzige seiner Art an Deutschen Universitäten. Im Gegensatz zu einer großen Zahl von Veranstaltungen im Umfeld des Mainstream-Themas Meditation legten wir nicht nur Wert auf die praktische Gestaltung sondern auch auf die Theoretische Dimension des Themas Meditation und es war uns wichtig, dass dies ein normales Lehrmodul war wie alle anderen Module.

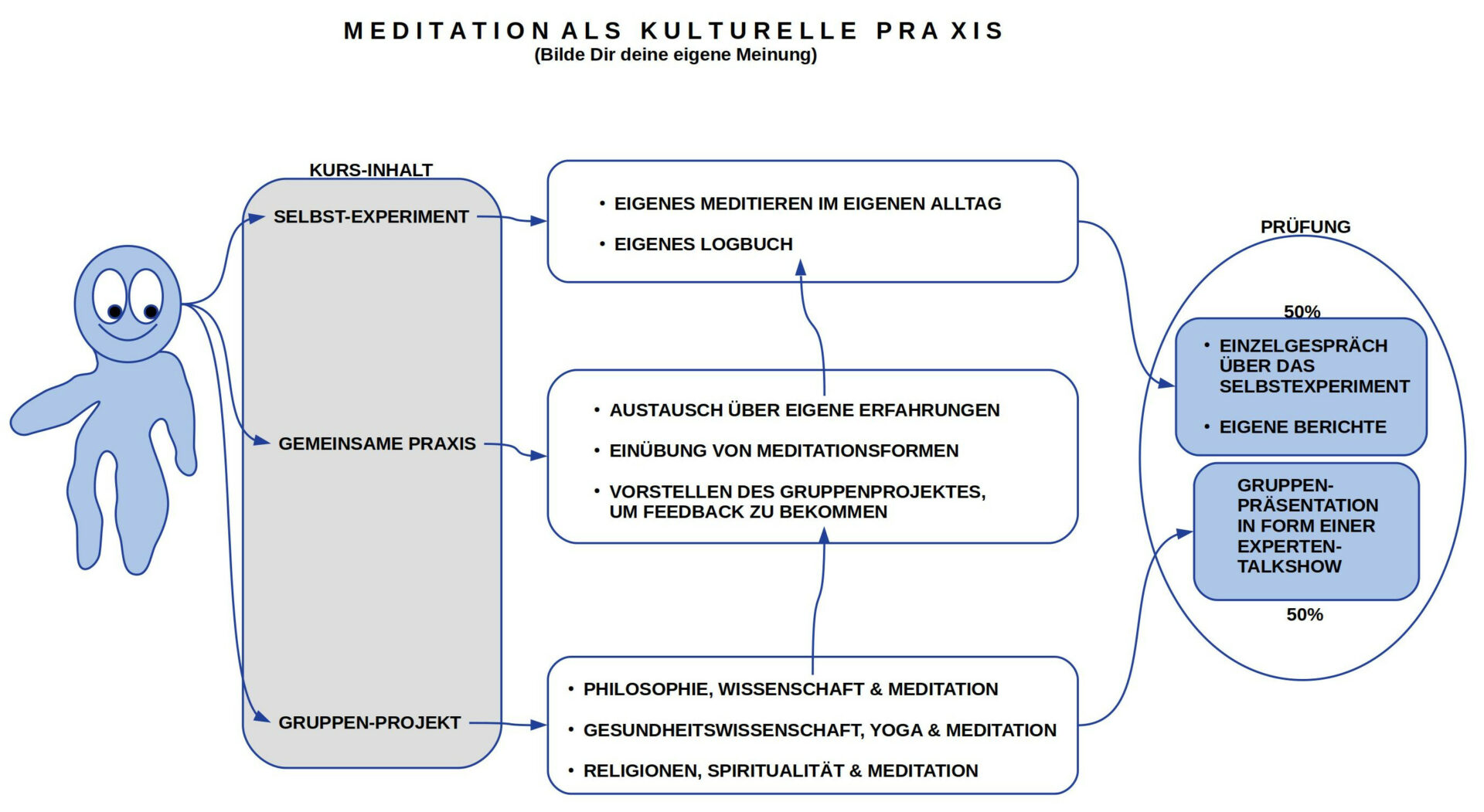
Konzept des Lehrmoduls Meditation als Kulturelle Praxis an der FUAS von SS2017 – WS2021. Im SS2017 Gab es statt des Themas Gesndheitswissenschaften, Yoga und Meditation das Thema Wirtschaft und Meditation.

Ohne auf die Details dieses Lehrmoduls weiter einzugehen (für mehr Informationen siehe [1]) möchte ich hier nur hervorheben, dass es nicht zuletzt auch die kontinuierliche Herausforderung dieses Moduls war, insbesonere die Konkretheit im Gegenüber zu den Studierenden, aber auch zu meinem Kollegen Reiner Frey und der Kollegin Julia Lademann, die Fragen aufwarf, die ich sonst, im Alltag, vielleicht nicht so direkt und konkret weiter verfolgt hätte. Dazu kamen zwei Kongresse, die wir in diesem Zusammenhang veranstalten konnten. Es war für mich vor allem der zweite Kongress im Herbst 2019, der mich herausforderte, da ich meinen Beitrag mutig unter das Thema Kann Mystik rational sein? gestellt hatte, ohne zu wissen, wie die Antwort ausfallen würde.(siehe: [2])

BEWUSSTWERDUNG – PHILOSOPHIE

(Letzte Änderung: 1.1.2021)

… Das Ich zeigt sich am Anderen. Festes im Fließenden. Konkretes und Allgemeines. Zufall und Muster. Erinnerung als Befreiung vom Jetzt. Schall mit Bedeutung. Ich denke. Wahrheit. Geist. Bewusstsein als Gefängnis. Wirksame Verschränkungen: strukturell-biologisch, strukturell-semantisch, strukturell-gesellschaftlich, digital, …

DIE GROSSEN TRANSFORMATIONEN

(Letzte Änderung: 1.1.2021)

… Die Erde hat eine Geschichte. Die Erde im Universum. Das Ereignis des Lebens im Nirgendwo. Das Leben als galaktischer Supercomputer. Homo sapiens nach 3.8 Milliarden Jahren Entwicklungsleistung. Verschränkung als Dimension der Entwicklung über Komplexität hinaus, …

HOMO SAPIENS – KIPP-PUNKT DER EVOLUTION

(Letzte Änderung: 1.1.2021)

… Ein Hoffnungsträger ohne Hoffnung. Ein galaktisches Genie in einer Wolke von Dummheit. Eine Freiheit, die vor sich hintaumelt. Chance Vielfalt als Bedrohung. Die Kunst der nachhaltigen Verschränkung: materiell, psychisch, gesellschaftlich, semantisch, wissensmäßig, Leitgedanken, prozesshaft, …

UNIVERSUM DES SINNS

(Letzte Änderung: 1.1.2021)

… Die eine Welt als Sinfonie von vielen Welten. Sinn im Kleinen wie im Großen. Welchem Sinn öffnen wir uns? …

UNBEKANNTE ZUKUNFT?

(Letzte Änderung: 1.1.2021)

… Die Gegenwart strömt in die Körper, die Gehirne machen daraus Vergangenheit. In der Erinnerung erwächst Differenz, zeigt sich virtuelle Zeit. Virtuelle Zeit erlaubt sowohl die Rekonstruktion der vergangenen Zeit wie auch von Gestalten einer Welt, die es noch nicht gibt: mögliche virtuelle Zukünfte. Die Gehirne und Körper (mit ihren Genen) sind realer Teil eines realen Prozesses. Unsere virtuellen Zukünfte können durch den Körper auf den realen Prozess einwirken. Was entsteht aus allem? Können wir nur zerstören? Welche Zukunft ist möglich? Wann fangen wir an, ernsthaft miteinander zu reden, statt uns gegenseitig zu quälen, uns umzubringen, und das Wunder des Lebens im großen Stil zu zerstören?…

Jede Frage entsteht in ihrem spezifischen Frageraum. Die Antwort kann jenseits dieses Raumes liegen, in den Bedingungen dieses Raumes. In den letzten 100 – 350 Jahren hat die Menschheit angefangen, mehr und mehr Aspekte ihrer eigenen Bedingtheit sichtbar zu machen. Dies verschiebt viele alten vertrauten Bilder. Die meisten alten Werte passen nicht mehr, behindern uns. Die neuen Bilder haben aber noch keine wirklich integrative Kraft entfaltet, wirken aufgesplittert, werden instrumentalisiert für Partikular-Interessen… nachhaltige Verschränkung geht anders …

MYSTIK: DAS ANDERE ANDERE

(Letzte Änderung: 1.1.2021)

… Das Ich und das Andere lernen sich kennen. Außerhalb des Körpers und innerhalb des Körpers. Emergenz durch Komplexität und Verschränkungen. Veränderung durch Energie. Das Andere zum bekannten Anderen: Es passiert, ohne eine Vorleistung von uns, schon immer, auch jetzt, und …. Freiheit, Liebe, Wissen … sind Erscheinungsweisen des Anderen Anderen … das grundlegende Mehr zu Allem … die notwendigen Verschränkungen des möglichen zukünftigen Lebens sind keine Automatismen. Sie verlangen nachhaltige Emotionen, solche die im Anderen Anderen verankert sind ….

LEBENS-MATRIX

(Letzte Änderung: 1.1.2021)

Zukunft braucht gemeinsame Hoffnung; Miteinander braucht Liebe; Wissen braucht Forschung; Handeln braucht Training und reale Welt; Energie-Materie … Ziel ist das Leben, in dem alles nachhaltig seinen Platz hat… im Universum und darüber hinaus … der einzelne alleine vermag dies nicht; es braucht viele neue Formen von Verschränkungen, die alles integrieren und doch maximale Freiheit ermöglichen, … die ca. 137 Billionen (10^12) Zellen, die unseren Körper samt Darmflora bilden, haben ca. 3.5 Milliarden (10^9) Jahre gebraucht, um ihre aktuelle Form der Verschränkung zu finden. Bislang übersteigt dieses biologische Wunder unser Verstehen noch deutlich. Wir als homo sapiens haben ca. 200.000 bis 300.000 Jahre gebraucht, um unsere heutigen Verschränkungen mittels Handeln und Sprache in vielen Bereichen zu entwickeln: Ernährung, Miteinander, Technik, Medizin, Wissen, … Die letzten 100 Jahren wirken wie eine Explosion, aber der Gesamtzustand wirkt nicht überzeugend. Entscheidende Bestandteile scheinen zu fehlen… alleine zu wissen ist wichtig, aber nur miteinander Wissen führt weiter, miteinander Fühlen … Sekten, Verschwörungs-An

Universelles Postskript: Sage mir bitte Bescheid, wenn Du angekommen bist …

QUELLENNACHWEISE

[1] Die Anfänge dieses Moduls samt dem ‚Zeitgeist‘ wurden beschrieben in dem Buch: Frank E.P.Dievernich, Gerd-Dietrich Döben-Henisch, Reiner Frey, Bildung 5.0: Wissenschaft, Hochschulen und Meditation. Das Sebstprojekt, Verlag: Beltz Juventa, Weinheim (DE), 2019

[2] Gerd-Dietrich Döben-Henisch, Kann Mystik rational sein?, in: Reiner Frey (Ed.), Meditation und die Zukunft der Bildung, Verlag: Beltz Juventa, Weinheim (DE), 2020, SS.108-123

DER AUTOR

Einen Überblick über alle Beiträge von Autor cagent nach Titeln findet sich HIER.

MEMO PHILOSOPHIE JETZT – WERKSTATTGESPRÄCH – 27.November 2016

Antike Philosophie, Aristoteles, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsmaterial, Mittelalter, Philosophie, Philosophie des Mittelalters, Philosophiewerkstatt, Philosophiewerkstatt, Semantik, Sprache, Sprachliche Äußerung, Sprachmaterial, Sprachspiel, Sprecher, Werkstattgespräch, Zeichen, Zeichenbenutzer, Zeichenmaterial

EINLADUNG

  1. Entsprechend der Einladung war das Thema dieses Treffens dieses Mal nicht das Fühlen (im philosophischen Sinne), sondern das Denken, unser eigenes Denken.

EINSTIMMUNG

  1. Jeden Tag benutzen wir unser Denken, indem wir mit anderen direkt kommunizieren oder indem wir jemandem etwas schreiben oder von jemand anderem etwas lesen/ hören.
  2. Aber was tun wir da, wenn wir mit anderen direkt kommunizieren?
  3. Die Frage ist nicht neu und hat schon viele Menschen vor uns bewegt.
  4. In einem kleinen historischen Blitzlicht wurde anhand wichtiger Philosophen und Denkern ein Zeitstrahl eingeblendet, der von Platos Geburt bis zur Gegenwart reichte (siehe Bild 1).

Zeittaffel von Plato bis zur Gegenwart
BILD 1: Zeittaffel von Plato bis zur Gegenwart

  1. Aus der Breite der (antiken) griechischen Philosophie waren stellvertretend nur die Namen der beiden bekanntesten griechischen Denker Plato und Aristoteles angeführt. Es dauerte ca. 600 – 800 Jahre, bis einige wenige Werke von Aristoteles im römischen Reich eine Übersetzung fanden, die bis ins Mittelalter wirkten.
  2. Im Mittelalter – hier abgebildet in der Spanne zwischen ca. 735 und 1360, also ca. 600 Jahre – gab es erst die Phase der direkten Aufnahme der wenigen aristotelischen Texte (zusammen mit Werken von Porphyr, Victorinus und Boethius); aus der intensiven Kommentierung entstanden zunehmend eigene, neue Positionen, die am Ende des 14.Jahrhunderts zu dem führte, was dann später neue empirische Wissenschaft, neue Logik und Mathematik bzw. neue Philosophie genannt wurde.
  3. Der Überblick machte dann einen Sprung in die letzten 150 Jahre bis zur Gegenwart.
  4. Der Überblick beginnt mit Bréal, der als Begründer der Idee einer Semantik gilt, der Lehre von der sprachlichen Bedeutung. Aus der Vielzahl der hier einschlägigen Denker und Denkerinnen folgt eine Auswahl der besonders bekannten Namen (teilweise mit Angabe der hier einschlägigen Werke).
  5. Allerdings, wie neuere Studien zum Mittelalter zeigen, sind viele der Ideen, die heute als neu daher kommen, im Mittelalter zumindest angedacht worden. Während im neuzeitlichen Denken des 20.Jahrhunderts die formalen Aspekte des Denkens und Sprechens stark bis fast vollständig von den assoziierten Inhalten (Bedeutungen) losgelöst erscheinen, hat das Mittelalter noch versucht, die Ausdrucksstrukturen und die Logik in ihrer intensiven Wechselwirkung zu denken. So sind z.B. die google-Algorithmen zur Analyse von Texten (und Bildern und …) heute ausschließlich an den formalen Ausdruckselementen orientiert; ein Bezug zu assoziierten Bedeutungen, wie sie jeder normale Sprecher-Hörer benutzt, fehlt vollständig. Dieser Bezug ist mit den bekannten Algorithmen auch nicht zu bekommen.
  6. Nach dieser blitzlichtartigen Einbettung der aktuellen Situation in den übergreifenden Denkkontext gab es die ‚individuelle Fühlpause‘ (manche nennen dies Meditation). Jeder konnte für sich – wie auch immer – 20 Min meditieren und sich anschließend Notizen machen.
  7. Wir stiegen dann in die erste Diskursrunde ein.(Siehe Bild 2)

PhJ Werkstattgespraech 27.November 2016 im INM - Gedankenskizze
BILD 2: PhJ Werkstattgespraech 27.November 2016 im INM – Gedankenskizze

START MIT EINER ÄUSSERUNG

  1. Für das gemeinsame Gedankenexperiment gab es zwei Leitfragen, von denen wir letztlich nur die erste ansatzweise bearbeiten konnten: FRAGE1: WIE HÄNGT EIN SPRACHLICHER AUSDRUCK MIT SEINER BEDEUTUNG ZUSAMMEN?
  2. Das Experiment begann damit, dass ein Teilnehmer aus der Runde spontan eine Äußerung macht: „Es ist behaglich“.
  3. Anhand dieser sprachlichen Äußerung entwickelte sich ein lebhaftes und intensives Gespräch, in dem jeder immer neue Aspekte beisteuerte.
  4. Wie man aus dem Bild 2 entnehmen kann, gab es zunächst mal Äußerungen von anderen TeilnehmernInnen, wie man diese anderen es formuliert hätten (siehe Bild 2).
  5. Daraus ergab sich, dass eine aktuelle, konkrete Äußerung in Beziehung zu setzen ist zum jeweiligen Sprecher bzw. Hörer. Je nach Sprecher empfindet dieser den Raum mit seiner für alle gleichen Temperatur entweder zu warm (also nicht behaglich), gerade richtig (z.B. behaglich) oder ganz anders.
  6. Außerdem empfanden manche Teilnehmer als Hörer die Allgemeinheit des Ausdrucks („Es ist“) zu vage. Lieber hätten sie gehört, dass der Sprecher das konkreter sagt, mehr über sich selbst („Ich empfinde es…“), was dem Hörer eher die Möglichkeit gibt, die Situation einzuschätzen. In der allgemeinen, unbestimmten Formulierung konnte es klingen, als ob der Sprecher für sich in Anspruch nimmt, auch für die anderen zu sprechen. Das fordert evtl. Widerspruch heraus…
  7. Dann wurde darauf aufmerksam gemacht, dass die Art der sprachlichen Äußerungen unterschiedliche Muster zulässt. Neben sachlicher Feststellung/ Behauptung gibt es auch einfache Ausrufe, Fragen, Befehle, Versprechen usw.
  8. Weitere Aspekte kamen ins Spiel: die Körpersprache des Sprechers. Wie steht diese im Verhältnis zu dem, was er sagt.
  9. Mit Beispielen aus eigenen Sprecherfahrungen wurde thematisiert, wie jemand von ganz vielen verschiedenen Gewohnheiten, Regeln, gesellschaftlichen Erwartungen in seinen Äußerungen gesteuert sein kann. Der Begriff der Rolle wurde eingeführt. Die Gesamtheit der wirkenden Regeln und Erwartungen können in der jeweiligen Situationen normativ wirken: jemand hat in einer bestimmten Situation bestimmte Gefühle, muss aber als Elternteil in diesem Moment eine gewisse Verantwortung wahrnehmen, entsprechend ein Therapeut in einem Beratungsgespräch, ein Lehrer in einer Unterrichtssituation, usw.
  10. Angeregt von Wittgenstein brachte ein Teilnehmer auch das Wort Sprachspiel in den Diskurs ein. Eine einzelne isolierte sprachliche Äußerung allein ist oft/ meistens nicht verständlich ohne die Einbettung in die Situation, ohne das Wechselspiel zwischen den Beteiligten, ohne dass alle Beteiligten in der Situation bestimmten (unterstellten) Regeln folgen.
  11. Ferner spielt der zeitliche Ablauf eine Rolle: was war vorher? So erwähnten einige TeilnehmerInnen, dass sie die vorausgehende individuelle Fühlzeit (Meditation) als sehr angenehm, beruhigend, entspannend erlebt hatten und danach ganz anders in den Diskurs eingestiegen sind.

DENKEN ÜBER DAS DENKEN

  1. Dies führte im Verlauf der zweiten Diskursrunde dann zum Versuch, das bislang Gesagte aus einer mehr reflektierenden Position nochmals zu betrachten. Anhand der Frage 1 gab es mehrere Anregungen des Gesprächsleiters, die Erzählperspektive des Teilnehmers mal zu verlassen und über den Diskurs zu reden. Erst als im unteren Teil von Bild 2 Ansätze einer theoretischen Modellbildung skizziert wurden, in der der Sprecher-Hörer als ein abstrakter Kreis erschien, der verschiedene sinnliche Wahrnehmungen hat, verschiedene Motive/ Interessen sowie unterschiedliche Erinnerungen/ erworbene Kompetenzen, setzte sich ansatzweise der Gedanke durch, dass die Ausdruckselemente (gesprochene Laute, geschriebene Zeichen, bestimmte Gesten,…) nicht automatisch, von vornherein, mit etwas anderem, dem, was dann Bedeutung verleiht, assoziiert sind. Man kann etwas sehen (einen Tisch im Zimmer) und etwas hören (einen sprachlichen Ausdruck ‚Tisch‘). Ohne dass man notwendigerweise den gesprochenen Ausdruck ‚Tisch‘ mit einem gesehenen Objekt (Tisch) assoziiert. Allein die Vielzahl der unterschiedlichen Sprachen zeigt, dass der deutsche Ausdruck für Russen, Chinesen, Spanier, Nigerianer, …. nicht zwingend ist. Sie haben das Problem anders gelöst.
  2. Ein Teilnehmer betonte mehrfach, dass man das Sprachgeschehen nicht in seine Bestandteile auflösen könne/ sollte, da man es ansonsten nicht verstehen würde. Mit Hinweis auf das (noch sehr primitive) Modell wurde erläutert, dass das sich Bewusstmachen der unterschiedlichen Komponenten, die in der interne Maschinerie des Sprecher-Hörers (letztlich im Gehirn) solch ein dynamisches Verhalten ermöglichen, kein Gegensatz sein muss zu einem holistischen Blick auf ein dynamisches Sprachgeschehen, eingebettet in Situationsfolgen. Das Zustandekommen von Assoziationen der unterschiedlichsten Arten in komplexen Handlungsfolgen ist gerade der Kern dessen, was man Lernen nennt. Im Lernprozess fließen alle diese unterschiedlichen Komponenten zusammen (aber nicht zwangsweise!).

AUSBLICK MIT FRAGEN

  1. Gegen Ende stellten sich dann viele neue Fragen.
  2. Z.B. die Frage nach den realen, konkreten Objekten in der Sprechsituation und der Frage, ob und wie diese als abstrakte Objekte im Kopf sein können, auch wenn sie in der konkreten Situation nicht mehr vorkommen. (So kann man ja über Gegenstände, Objekte auch in ihrer Abwesenheit sprechen).
  3. Eng damit zusammenhängend die Frage nach allgemeinen Begriffen. Wir reden von Tischen, jeder konkrete Tisch ist aber anders; entsprechend Begriffe wie Stuhl, Tasse, Mensch usw.
  4. Andere Fragestellungen ergaben sich aus dem Eindruck, dass sich die Sprache verrohen würde, vereinfachen.
  5. Oder: welche Bedeutung kommt der Handschrift zu? Kann man auf sie verzichten ohne negative Wirkung auf das Sprachvermögen/ das Sprachverstehen?
  6. Schließlich der Wunsch, dass die einzelnen noch mehr Beispiele aus ihrer persönlichen Sprachlerngeschichte beisteuern, da die Beispiele, die während des Gesprächs spontan erzählt wurden, sehr aufschlussreich waren.

Einen Überblick über alle Einträge zur Philosophiewewrkstatt nach Titeln findet sich HIER.

Einen Überblick über alle Themenbereiche des Blogs finden sich HIER.

PHILOSOPHIESOMMER 2016 IN DER DENKBAR FRANKFURT

Alltagswissen, Antike Philosophie, Aristoteles, Denken philosophisch, empirische Wissenschaft, Erkenntnistheorie, Geisteswissenschaften, Kognitionswissenschaft, Kommunizierbarkeit von philosophischen Inhalten, Musikexperiment - philosophisches, netzbasiertes verteiltes Wissen, Phänomenologische Philosophie, Philosoph, Philosophie, Philosophie bewusstseinsbasiert, Philosophiesommer, Philosophiewerkstatt, PHILOSOPHY-IN-CONCERT, Wahr und Falsch, Werkstattgespräch, Werte, Wertvorstellungen, Wirtschaft, Wissen, Wissenschaft, Wissenschaftskritik, Zeit, Zufall, Zukunft

Alltag, Visionen der Wissenschaft, und die antike Philosophie: müssen hier Köpfe rollen oder gibt es neue gedankliche Fusion?

Sind Sie neugierig, oder meinen Sie, etwas beitragen zu können?

Kommen Sie dazu.

Geben Sie ihrer Eitelkeit drei Stunden Urlaub und lassen Sie zu, dass Sie in der Andersartigkeit vielleicht etwas Neues entdecken.

ORT:

DENKBAR Frankfurt
Spohrstrasse 46a

(Achtung: Parken schwierig! Man muss wirklich im Umfeld suchen)

PROGRAMMFORMAT

Moderation: Gerd Doeben-Henisch

16:00 Begrüßung

16:05 Kleine Performance aus dem PHILOSOPHY-IN-CONCERT Experiment

16:15 Eingangsüberlegungen

16:30 Erste offene Gesprächsrunde (simultan Erstellung eines Begriffsnetzwerkes)

17:30 Blubberpause (Jeder kann mit jedem reden; Essen und Trinken)

18:00 Zweite offene Gesprächsrunde (simultan Erstellung eines Begriffsnetzwerkes)

18:45 Schlussstatements

19:00 Ende

Langsames Wegdiffundieren der Teilnehmer ….

ERINNERUNGEN…

In der Regel erscheint im Anschluss an eine Sitzung ein Bericht im Blog cognitiveagent.org, der auch Gelegenheit bietet, sich durch Kommentare oder eigene Beiträge an der Diskussion zu beteiligen.

INHALTLICHE LINIE

Da der Gesprächsprozess – abhängig von den Teilnehmern! – seine eigene Dynamik gewinnt, lässt sich keine genaue Prognose für alle kommenden Themen geben.

Das Rezept für den Start orientiert sich einmal an unseren alltäglichen Erfahrung einer Menschheit im Fiebertaumel zwischen Gewalt, Krieg, Katastrophen auf der einen Seite, eingespannt in ein umfassendes Räderwerk von Wirtschaft, Verwaltungen, Medienströmen, Politikbetrieb, Anwachsen von ‚tiefem Staat‘ mit mittlerweile grenzenloser Überwachung andererseits; dazu eine scheinbar entfesselte Wissenschaft, die – abgeschottet von der Öffentlichkeit – immer neue Details der Materie enthüllt, den Menschen als biochemische Masse sieht, deren Tage gezählt sind, und in automatisierten Produktionsprozessen denkt, die mit bekannten Wertesystemen kaum noch etwas zu tun haben. Und dann, man wagt es kaum zu sagen, gab es einen alten, sehr alten Philosophen, der mindestens 1800 Jahre lang das Denken In ganz Europa (Westen wie Osten; christliche Theologie genauso wie die islamische Theologie!) geprägt hat, Aristoteles, der heute auf allen Gebieten als abgeschrieben gelten kann. Und doch, schaut man sich die großen Lücken an, die die moderne Wissenschaft mit sich herumschleppt, kann man ins Grübeln kommen. Die Zukunft ist niemals einfach nur die Wiederholung des Gestern. Aber sie ist auch niemals das total ganz andere. Die biologische Evolution praktiziert das Modell der Zähmung des Zufalls durch Erinnerung; das Ergebnis nach ca. 4 Mrd Jahren sind u.a. wir, der homo sapiens. Es ist schwer zu verstehen, bis heute. Manche wollen es auch gar nicht verstehen…

ARCHIV

Wer sich für die bisherigen philosophischen Gespräche unter der Überschrift ‚Philosophiewerkstatt‘ interessiert, ist eingeladen, die Erinnerungsseite zu besuchen. Hier gibt es Berichte von den zurückliegenden Diskursen.

VORSCHAU TERMINE PHILOSOPHIEWERKSTATT FEBRUAR – MAI 2016

Antike Philosophie, Aristoteles, Aristoteles, Augustinus, Denken philosophisch, Erkenntnistheorie, Geist, Geist - Künstlicher, Philosoph, Philosophie, Philosophie klassische, Philosophiewerkstatt, PHILOSOPHY-IN-CONCERT, Platon, Seele, Selbstorganisation des, Sokrates, sokratische Methode, Thomas von Acquin

Da der Start zur neuen Serie etwas ‚ruckelig‘ war (Krankheit, Weihnachtsfeiertage, Terminkollisionen), hier – in Rücksprache mit Reinhard Graeff von der DENKBAR – der Versuch eines Neustarts für die Zeit Februar – Mai 2016, jeweils 2.Sonntag im Monat 16:00 – 19:00h:

TERMINE

VORGEHENSWEISE

Wir werden den bisherigen dialogischen (sokratischen) Stil der Bedeutungsfindung beibehalten, aber ergänzt um folgende Momente:

  • Zu Beginn eine thematisch passende Eingangsmusik ca.5-8 Min aus dem PHILOSPHY-IN-CONERT Programm des Emerging Mind Projektes
  • Vorstellung einer klassischen Position aus der Geschichte der Philosophie (Platon, Aristoteles, Augustinus, Thomas v.Acquin) ca. 10 – 15Min im Umfeld der Begriffe ‚Geist‘ und ‚Seele‘.
  • Gesprächsprozess zum vertiefenden Verständnis und geleitet von der Frage, ob und wie sich diese Positionen im Lichte heutiger Philosophie und Wissenschaft noch aufrecht erhalten lassen; falls nicht, was folgt daraus?
  • Im Anschluss an die Sitzung wird wie gewohnt ein Memo der Sitzung im Blog PHILOSOPHIE JETZT veröffentlicht. Jeder ist eingeladen, diese Darstellung mit eigenen Beiträgen zu ergänzen.

SPEZIELLER HINWEIS

Für alle die es interessiert, am

Mi, 20.Januar 2016, 19:30h

findet die Eröffnung des Emerging Mind Projektes im Institut für Neue Medien (INM) (Frankfurt) statt in Form eines Werkstattgesprächs. Das Emerging Mind Projekt (EMP) ist ein philosophisch motiviertes Projekt zur theoretischen und praktischen Erforschung der Zukunft von Menschen und intelligenten Maschinen. Es kooperiert eng mit der Emergent Life Academy (ELA), die diese Frage in dem größeren Kontext einer allgemeinen Entwicklungswissenschaft stellt, ebenfalls mit einem starken philosophischen Einschlag.

PHILOSOPHIEWERKSTATT BISHER

Einen Überblick über alle Beiträge zur Philosophiewerkstatt nach Themen findet sich HIER

BUCHPROJEKT 2015 – Zwischenreflexion 23.August 2015 – INFORMATION – Jenseits von Shannon

Adriaans, Allgemeine, Bedeutung, Biologische Information, Boltzmann - Ludwig, Deacon, Dekodieren, Empfänger, Erkenntnistheorie, Erweiterte statistische Informationstheorie, Falsifizierbarkeit (Popper), Floridi, Godfrey-Smith, Information, Information1 - Shannon, Information2 - Bedeutungsrelation, Informationsstrukturen, Informationstheorie, Kodieren, Kommunikationsereignis, Kommunikationskanal, Mathematische, Maynard Smith, Molekularbiologie, Ontogenese, Ontologie, Philosophie, Philosophy of Science, Phylogenese, Semantische Information, Sender, Shannon 1948, Statistische Informationstheorie, Sterelny, Theorie, Theorie - formale, Theorie biologische, Theorie empirische, Theorie phänomenologische

Der folgende Beitrag bezieht sich auf das Buchprojekt 2015.

VORHERIGE BEITRÄGE

1. Im Beitrag von John Maynard Smith hatte dieser Kritik geübt an der Informationstheorie von Shannon. Dabei fokussierte er im wesentlichen auf die direkte Anwendung des Shannonschen Begriffs auf die informationsvermittelnden Prozesse bei der Selbstreproduktion der Zelle, und er konnte deutlich machen, dass viele informationsrelevanten Eigenschaften bei dem Reproduktionsprozess mit dem Shannonschen Informationsbegriff nicht erfasst werden. Anschließend wurde ein Beitrag von Terrence W.Deacon diskutiert, der den Shannonschen Informationsbegriff als Ausgangspunkt nutzte, den er it dem Entropiebegriff von Boltzmann verknüpfte, von dort die Begriffe thermodynamisches Ungleichgewicht, Arbeit und Evolution nach Darwin benutzte, um die Idee anzudeuten, dass jene Zustände in einem System, die bedeutungsrelevant sein könnten (und von Shannon selbst nicht analysiert werden) in Interaktion mit der Umwelt entstanden sind und entstehen.

ZWISCHENSTAND
2. Was sowohl bei Maynard Smih wie auch bei Deakon auffällt, ist, dass sie sich wenig um den möglichen Kontext des Begriffs ‚Information‘ bemühen. Wie wurde der Begriff der Information im Laufe der Ideengeschichte verstanden? Welche Besonderheiten gibt es in den verschiedenen Disziplinen?

HISTORISCH-SYSTEMATISCHE PERSPEKTIVE

3. In einem umfangreichen und detailliertem Überblick von Pieter Adriaans (2012) in der Standford Encyclopedia of Philosophy findet man ein paar mehr Zusammenhänge.

4. Zwar heißt es auch hier mehrfach, dass ein erschöpfender Überblick und eine alles umfassende Theorie noch aussteht, aber ausgehend von der antiken Philosophie über das Mittelalter, die Renaissance bis hin zu einigen modernen Entwicklungen findet man wichtige Themen und Autoren.

5. Zusammenfassend sei hier nur festgestellt, dass Aspekte des Informationsbegriffs auf unterschiedlich Weise bis zum Ende des 19.Jahrhunderts feststellbar sind, ohne dass man von einer eigentlich Philosophie der Information oder einer Informationstheorie im modernen Sinne sprechen kann. Als grobe Koordinaten, die den Ausgangspunkt für die neuere Entwicklung einer Informationstheorie markieren, nennt Adriaans (i) Information als ein Prozess, der Systeme prägen/ formieren/ informieren kann; (ii) Information als ein Zustand, der sich bei einem System einstellt, nachdem es informiert wurde; (iii) Information als die Fähigkeit eines Systems, seine Umgebung zu prägen/ formen/ informieren.

6. Weiterhin identifiziert er zusammenfassend einige Bausteine der modernen Informationstheorie: (i) Information ist ‚extensiv‘ insofern die Bestandteile in das übergreifende Ganze eingehen und sie vermindert Unsicherheit; (ii) man benötigt eine formale Sprache zu ihrer Darstellung; (iii) ein ‚optimaler‘ Kode ist wichtig; (iv) die Verfügbarkeit eines optimierten Zahlensystems (binär, Stellen, Logarithmus) spielte eine Rolle; ausgehend von konstituierenden Elementen die Idee der Entropie in Kombination mit der Wahrscheinlichkeit; (v) die Entwicklung einer formalen Logik für Begriffe wie ‚Extension/ Intension‘, ‚Folgerung‘, ‚Notwendigkeit‘, ‚mögliche Welten‘, ‚Zustandsbeschreibungen‘ und ‚algorithmische Informationstheorie‘.

7. Andere wichtige Themen sind (i) Information als Grad der Widerlegbarkeit (Popper); (ii) Information in Begriffen der Wahrscheinlichkeit (Shannon); (iii) Information als Länge des Programms (Solomonoff, Kolmogorov, Chaitin).

SHANNON ERSCHEINT ÜBERMÄCHTIG

8. Was man bei Adriaans vermisst, das ist der Bezug zur semantischen Dimension. Hierzu gibt es einen anderen sehr umfangreichen Beitrag von Floridi (2015), auf den auch Adriaans verweist. Floridi behandelt die Frage der Semantischen Information quantitativ sehr ausführlich, inhaltlich aber beschränkt er sich weitgehend auf eine formale Semantik im Umfeld einer mathematischen Informationstheorie auf der Basis von Shannon 1948. Dies verwundert. Man kann den Eindruck gewinnen, dass die ‚konzeptuelle Gravitation‘ des Shannonschen Modells jede Art von begrifflicher Alternative im Keim erstickt.

BEFREIUNG DURCH BIOLOGIE

9. Bringt man die Informationstheorie in das begriffliche Gravitationsfeld der Biologie, insbesondere der Molekularbiologie, dann findet man in der Tat auch andere begrifflich Ansätze. Peter Godfrey-Smith und Kim Sterelny (2009) zeigen am Beispiel der Biologie und vieler molekularbiologischer Sachverhalte auf, dass man das enge Modell von Shannon durch weitere Faktoren nicht nur ergänzen kann, sondern muss, will man den besonderen biologischen Sachverhalten Rechnung tragen. Allerdings führen sie ein solches Modell nicht allgemein aus. Kritiker weisen darauf hin, dass solche zusätzlichen Abstraktionen die Gefahr bieten – wie in jeder anderen wissenschaftlichen Disziplin auch –, dass sich Abstraktionen ‚ontologisch verselbständigen‘; ohne erweiternde Begrifflichkeit kann man allerdings auch gar nichts sagen.

THEORIE A LA BOLTZMANN VOR MEHR ALS 100 JAHREN

10. Diese ganze moderne Diskussion um die ‚richtigen formalen Modelle‘ zur Erklärung der empirischen Wirklichkeit haben starke Ähnlichkeiten mit der Situation zu Zeiten von Ludwig Boltzmann. In einer lesenswerten Rede von 1899 zur Lage der theoretischen Physik ist er konfrontiert mit der stürmischen Entwicklung der Naturwissenschaften in seiner Zeit, speziell auch der Physik, und es ist keinesfalls ausgemacht, welches der vielen Modelle sich in der Zukunft letztlich als das ‚richtigere‘ erweisen wird.

11. Boltzmann sieht in dieser Situation die Erkenntnistheorie gefragt, die mithelfen soll, zu klären, welche Methoden in welcher Anordnung einen geeigneten Rahmen hergeben für eine erfolgreiche Modellbildung, die man auch als theoretische Systeme bezeichnen kann, die miteinander konkurrieren.

12. Mit Bezugnahme auf Hertz bringt er seinen Zuhörern zu Bewusstsein, „dass keine Theorie etwas Objektives, mit der Natur wirklich sich Deckendes sein kann, dass vielmehr jede nur ein geistiges Bild der Erscheinungen ist, das sich zu diesen verhält wie das Zeichen zum Bezeichneten.“ (Boltzmann 1899:215f) Und er erläutert weiter, dass es nur darum gehen kann, „ein möglichst einfaches, die Erscheinungen möglichst gut darstellendes Abbild zu finden.“ (Boltzmann 1899:216) So schließt er nicht aus, dass es zum gleichen empirischen Sachverhalt zwei unterschiedliche Theorien geben mag, die in der Erklärungsleistung übereinstimmen.

13. Als Beispiel für zwei typische theoretische Vorgehensweisen nennt er die ‚Allgemeinen Phänomenologen‘ und die ‚Mathematischen Phänomenologen‘. Im ersteren Fall sieht man die theoretische Aufgabe darin gegeben, alle empirischen Tatsachen zu sammeln und in ihrem historischen Zusammenhang darzustellen. Im zweiten Fall gibt man mathematische Modelle an, mit denen man die Daten in allgemeine Zusammenhänge einordnen, berechnen und Voraussagen machen kann. Durch die Einordnung in verallgemeinernde mathematische Modelle geht natürlich die Theorie über das bis dahin erfasste Empirische hinaus und läuft natürlich Gefahr, Dinge zu behaupten die empirisch nicht gedeckt sind, aber ohne diese Verallgemeinerungen kann ein Theorie nichts sagen. Es kann also nicht darum gehen, ’nichts‘ zu sagen, sondern das, was man theoretisch sagen kann, hinreichend auf Zutreffen bzw. Nicht-Zutreffen zu kontrollieren (Poppers Falsifizierbarkeit). Boltzmann bringt seitenweise interessante Beispiele aus der damals aktuellen Wissenschaftsdiskussion, auf die ich hier jetzt aber nicht eingehe.

WIE SHANNON ERWEITERN?

14. Stattdessen möchte ich nochmals auf die Fragestellung zurück kommen, wie man denn vorgehen sollte, wenn man erkannt hat, dass das Modell von Shannon – so großartig es für die ihm gestellten Aufgaben zu sein scheint –, bzgl. bestimmter Fragen als ‚zu eng‘ erscheint. Hier insbesondere für die Frage der Bedeutung.

15. Im Beitrag von Deacon konnte man eine Erweiterungsvariante in der Weise erkennen, dass Deacon versucht hatte, über die begriffliche Brücke (Shannon-Entropie –> Boltzmann-Entropie –>Thermodynamik → Ungleichgewicht → Aufrechterhaltung durch externe Arbeit) zu der Idee zu kommen, dass es in einem biologischen System Eigenschaften/ Größen/ Differenzen geben kann, die durch die Umwelt verursacht worden sind und die wiederum das Verhalten des Systems beeinflussen können. In diesem Zusammenhang könnte man dann sagen, dass diesen Größen ‚Bedeutung‘ zukommt, die zwischen Systemen über Kommunikationsereignisse manifestiert werden können. Ein genaueres Modell hatte Deacon dazu aber nicht angegeben.

16. Wenn Deacon allerdings versuchen wollte, diese seine Idee weiter zu konkretisieren, dann käme er um ein konkreteres Modell nicht herum. Es soll hier zunächst kurz skizziert werden, wie solch ein Shannon-Semantik-System aussehen könnte. An anderer Stelle werde ich dies Modell dann formal komplett hinschreiben.

SHANNON-SEMANTIK MODELL SKIZZE

17. Als Ausgangspunkt nehme ich das Modell von Shannon 1948. (S.381) Eine Quelle Q bietet als Sender Nachrichten M an, die ein Übermittler T in Kommunikationsereignisse S in einem Kommunikationskanal C verwandelt (kodiert). In C mischen sich die Signale S mit Rauschelementen N. Diese treffen auf einen Empfänger R, der die Signale von den Rauschanteilen trennt und in eine Nachricht M* verwandelt (dekodiert), die ein Empfänger D dann benutzen kann.

18. Da Shannon sich nur für die Wahrscheinlichkeit bestimmter Signalfolgen interessiert hat und die Kapazitätsanforderungen an den Kanal C, benötigt sein Modell nicht mehr. Wenn man aber jetzt davon ausgeht, dass der Sender nur deshalb Kommunikationsereignisse S erzeugt, weil er einem Empfänger bestimmte ‚Bedeutungen‘ übermitteln will, die den Empfänger in die Lage versetzen, etwas zu ‚tun‘, was der übermittelten Bedeutung entspricht, dann muss man sich überlegen, wie man das Shannon Modell erweitern kann, damit dies möglich ist.

19. Das erweiterte Shannon-Semantik Modell soll ein formales Modell sein, das geeignet ist, das Verhalten von Sendern und Empfängern zu beschreiben, die über reine Signale hinaus mittels dieser Signale ‚Bedeutungen‘ austauschen können. Zunächst wird nur der Fall betrachtet, dass die Kommunikation nur vom Sender zum Empfänger läuft.

20. Ein erster Einwand für die Idee einer Erweiterung könnte darin bestehen, dass jemand sagt, dass die Signale ja doch ‚für sich‘ stehen; wozu braucht man die Annahme weiterer Größen genannt ‚Bedeutung‘?

21. Eine informelle Erläuterung ist sehr einfach. Angenommen der Empfänger ist Chinese und kann kein Deutsch. Er besucht Deutschland. Er begegnet dort Menschen, die kein Chinesisch können und nur Deutsch reden. Der chinesische Besucher kann zwar sehr wohl rein akustisch die Kommunikationsereignisse in Form der Laute der deutschen Sprache hören, aber er weiß zunächst nichts damit anzufangen. In der Regel wird er auch nicht in der Lage sein, die einzelnen Laute separat und geordnet aufzuschreiben, obgleich er sie hören kann. Wie wir wissen, braucht es ein eigenes Training, die Sprachlaute einer anderen Sprache zweifelsfrei zu erkennen, um sie korrekt notieren zu können. Alle Deutschen, die bei einer solchen Kommunikation teilnehmen, können die Kommunikationsereignisse wahrnehmen und sie können – normalerweise – ‚verstehen‘, welche ‚anderen Sachverhalte‘ mit diesen Kommunikationsereignissen ‚verknüpft werde sollen‘. Würde der Chinese irgendwann Deutsch oder die Deutschen Chinesisch gelernt haben, dann könnten die Deutschen Kommunikationsereignisse in Chinesische übersetzt werden und dann könnten – möglicherweise, eventuell nicht 1-zu-1 –, mittels der chinesischen Kommunikationsereignisse hinreichend ähnliche ‚adere Sachverhalte‘ angesprochen werden.

22. Diese anderen Sachverhalte B, die sich den Kommunikationsereignissen zuordnen lassen, sind zunächst nur im ‚Innern des Systems‘ verfügbar. D.h. Die Kommunikationsereignisse S (vermischt mit Rauschen N) im Kommunikationskanal C werden mittels des Empfängers R in interne Nachrichten M* übersetzt (R: S x N —> M*), dort verfügt der Empfänger über eine weitere Dekodierfunktion I, die den empfangenen Nachrichten M* Bedeutungssachverhalte zuordnet, also I: M* —> B. Insofern ein Dolmetscher weiß, welche Bedeutungen B durch eine deutsche Kommunikationssequenz im Empfänger dekodiert werden soll, kann solch ein Dolmetscher dem chinesischen Besucher mittels chinesischer Kommunikationsereignisse S_chin einen Schlüssel liefern, dass dieser mittels R: S_chin —> M*_chin eine Nachricht empfangen kann, die er dann mit seiner gelernten Interpretationsfunktion I_chin: M*_chin —> B‘ in solche Bedeutungsgrößen B‘ übersetzen kann, die den deutschen Bedeutungsgrößen B ‚hinreichend ähnlich‘ sind, also SIMILAR(B, B‘).

23. Angenommen, der empfangenen Nachricht M* entspricht eine Bedeutung B, die eine bestimmte Antwort seitens des Empfängers nahelegt, dann bräuchte der Empfänger noch eine Sendeoperation der Art Resp: B —> M* und T: M* —> S.

24. Ein Empfänger ist dann eine Struktur mit mindestens den folgenden Elementen: <S,N,M*,B,R,I,resp,T> (verglichen mit dem ursprünglichen Shannon-Modell: <S,N,M*,-,R,I,-,T>). So einfach diese Skizze ist, zeigt sie doch, dass man das Shannon Modell einfach erweitern kann unter Beibehaltung aller bisherigen Eigenschaften.

25. Natürlich ist eine detaillierte Ausführung der obigen Modellskizze sehr aufwendig. Würde man die Biologie einbeziehen wollen (z.B. im Stile von Deacon), dann müsste man die Ontogenese und die Phylogenese integrieren.

26. Die Grundidee der Ontogenese bestünde darin, einen Konstruktionsprozess zu definieren, der aus einem Anfangselement Zmin das endgültige System Sys in SYS erstellen würde. Das Anfangselement wäre ein minimales Element Zmin analog einer befruchteten Zelle, das alle Informationen enthalten würde, die notwendig wären, um diese Konstruktion durchführen zu können, also Ontogenese: Zmin x X —> SYS. Das ‚X‘ stünde für alle die Elemente, die im Rahmen einer Ontogenese aus der Umgebung ENV übernommen werden müssten, um das endgültige system SYS = <S,N,M*,B,R,I,resp,T> zu konstruieren.

27. Für die Phylogenese benötigte man eine Population von Systemen SYS in einer Umgebung ENV, von denen jedes System Sys in SYS mindestens ein minimales Anfangselement Zmin besitzt, das für eine Ontogenese zur Verfügung gestellt werden kann. Bevor die Ontogenese beginnen würde, würden zwei minimale Anfangselemente Zmin1 und Zmin2 im Bereich ihrer Bauanleitungen ‚gemischt‘, um dann der Ontogenese übergeben zu werden.

QUELLEN

  1. John Maynard Smith (2000), „The concept of information in biology“, in: Philosophy of Science 67 (2):177-194
  2. Terrence W.Deacon (2010), „What is missing from theories of information“, in: INFORMATION AND THE NATURE OF REALITY. From Physics to Metaphysics“, ed. By Paul Davies & Niels Henrik Gregersen, Cambridge (UK) et al: Cambridge University Press, pp.146 – 169
  3. Bernd-Olaf Küppers 2010), „Information and communication in living matter“, in: INFORMATION AND THE NATURE OF REALITY. From Physics to Metaphysics“, ed. By Paul Davies & Niels Henrik Gregersen, Cambridge (UK) et al: Cambridge University Press, pp.170-184
  4. Luciano Floridi (2015) Semantic Conceptions of Information, in: Stanford Enyclopedia of Philosophy
  5. Jesper Hoffmeyer (2010), „Semiotic freedom: an emerging force“, in: INFORMATION AND THE NATURE OF REALITY. From Physics to Metaphysics“, ed. By Paul Davies & Niels Henrik Gregersen, Cambridge (UK) et al: Cambridge University Press, pp.185-204
  6. Stichwort Information in der Stanford Enyclopedia of Philosophy von Pieter Adriaans (P.W.Adriaans@uva.nl) (2012)
  7. Peter Godfrey-Smith, Kim Sterelny (2009) Biological Information“, in: Stanford Enyclopedia of Philosophy
  8. Hans Jörg Sandkühler (2010), „Enzyklopädie Philosophie“, Bd.2, 2., überarbeitete und erweiterte Auflage, Meiner Verlag, Hamburg 2010, ISBN 978-3-7873-1999-2, (3 Bde., parallel dazu auch als CD erschienen)
  9. Ludwig Boltzmann (1899), „Über die Entwicklung der Methoden der theoretischen Physik in neuerer Zeit“, in: „Populäre Schriften“, Leipzig:Verlag von Johann Ambrosius Barth, 1905, SS.198-227
  10. Lawrence Sklar (2015), Philosophy of Statistical Mechanics in Stanford Encyclopedia of Philosophy
  11. Schroedinger, E. „What is Life?“ zusammen mit „Mind and Matter“ und „Autobiographical Sketches“. Cambridge: Cambridge University Press, 1992 (‚What is Life‘ zuerst veröffentlicht 1944; ‚Mind an Matter‘ zuerst 1958)
  12. Claude E. Shannon, A mathematical theory of communication. Bell System Tech. J., 27:379-423, 623-656, July, Oct. 1948
  13. Claude E. Shannon; Warren Weaver (1949) „The mathematical theory of communication“. Urbana – Chicgo: University of Illinois Press.
  14. John Maynard Smith (2000), „The concept of information in biology“, in: Philosophy of Science 67 (2):177-194
  15. Noeth, W., Handbuch der Semiotik, 2. vollst. neu bearb. und erw. Aufl. mit 89 Abb. Stuttgart/Weimar: J.B. Metzler, xii + 668pp, 2000
  16. Monod, Jacques (1971). Chance and Necessity. New York: Alfred A. Knopf
  17. Introduction to Probability von Charles M. Grinstead und J. Laurie Snell, American Mathematical Society; Auflage: 2 Revised (15. Juli 1997)

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 22

Allquantor, Analytisch, Aristoteles, Avicenna, Beweis - logischer, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Schlussfigur, Schlussfolgern, Syllogismus - Konjunktiver

(Letzte Änderungen: Mi 15.Okt.2014, 12:17h)

VORGESCHICHTE
Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

1. Im letzten Beitrag entstand die Arbeitshypothese, dass aufgrund des ‚fließenden‘ Bedeutungsübergangs zwischen ‚echten‘ und ‚unechten‘ Objekten auf der Bedeutungsseite damit die Unterscheidung zwischen ‚Subjekt‘ (S) und ‚Prädikat‘ (P) auch fließend würde. Das würde die Unterscheidung ob die Terme ‚S‘ oder ‚P‘ sind aufheben. Anders ausgedrückt, die Terme in einer Schlussfigur erscheinen ‚invariant‘ bzgl. der Kategorisierung als ‚S‘ oder ‚P‘.

2. Verfolgt man den Gedanken der ‚Invarianz‘ weiter, dann sieht man sofort, dass die Anordnung der Prämissen 1 und 2 auch ‚invariant‘ ist gegenüber ‚Vertauschung‘. Hat man die Prämissen A1: (_ F M) und A2: (_M H) mit dem Muster, das die Schlussfigur 1 charakterisiert, dann erhält man durch Vertauschen der Reihenfolge A1: (_ M F) und A2: (_H M) die Schlussfigur 4 (die Avicenna nicht benutzt), und kann feststellen, dass diese Vertauschung nichts an der Bedeutungsstruktur und damit an der Folgerung ändert. Darüber hinaus sieht man, dass durch die Vertauschung der Prämissen auch die Quantoren der ersten und zweiten Prämisse gespiegelt wurden. Der ‚Wahrheitsgehalt‘ der Schlussfigur bleibt ‚erhalten‘.

Schlussfigur 1 mit Quantorenkombination 1-4 'gespiegelt' als Schlussfigur 4 mit Quantorenkombination 1-4, ebenfalls gespiegelt
Schlussfigur 1 mit Quantorenkombination 1-4 ‚gespiegelt‘ als Schlussfigur 4 mit Quantorenkombination 1-4, ebenfalls gespiegelt

3. Es lieg nahe, den ‚Spiegelungstest‘ auch mit den Schlussfiguren 2 und 3 vorzunehmen. Hier die Ergebnisse:

Alle Muster von Figur 2 samt inverse
Alle Muster von Figur 2 samt inverse

Alle Muster von Figur 3 samt Inverse
Alle Muster von Figur 3 samt Inverse

4. Man sieht, dass die Spiegelung in Form der Veränderung der ‚Abfolge‘ der Prämissen keine Wirkung auf den ‚Wahrheitsgehalt‘ besitzt. Dies wird verständlich, wenn man sich klar macht, dass die ‚Ausdrücke‘ E einer Sprache L ja nicht die ‚Bedeutung selbst‘ darstellen, sondern nur auf die Bedeutungsstrukturen ‚Bezug nehmen‘. Wie immer diese beschaffen sein mögen, die sprachlichen Strukturen ‚kodieren‘ diese nur. Und insoweit es sich bei den hier angesprochenen Sachverhalten um statische Beziehungsverhältnisse handelt, spielt die Abfolge der beschreibenden Äußerungen – zumindest in diesen Fällen — keine Rolle.

5. Fasst man alle Schlussfiguren (ohne ihre ‚bedeutungsgleichen‘ inversen Varianten) zusammen, dann erhält man folgende Tabelle:

Tabellarische Gesamtübersicht über alle Schlussfiguren 1-3 samt allen benutzten Quantorenkombinationen 1-11
Tabellarische Gesamtübersicht über alle Schlussfiguren 1-3 samt allen benutzten Quantorenkombinationen 1-11

6. Angesichts dieser vielen ‚Invarianzen‘ drängt sich verstärkt die Frage auf, was denn dann der ‚harte Kern‘ an Strukturen ist, an denen sich der ‚Wahrheitsgehalt‘ einer Folgerung orientiert.

7. Bislang hat sich schon herausgeschält, dass es um ‚Beziehungen zwischen Mengen‘ geht (welche Elemente in welchen Mengen vorkommen), und um Eigenschaften, die diesen Elementen ‚zugesprochen‘ werden.

8. Die Schlussfiguren 1-3 (bzw. 1-4) setzen in den Prämissen genau drei verschiedene Mengen F, H und M voraus, zwischen denen jeweils F und H eine Beziehung zu M haben. Insofern ist M der ‚Mittelterm‘ (und F und H sind die ‚äußeren‘ Terme). Gefragt wird dann immer nach der sich daraus resultierenden Beziehung zwischen F und H. Die ‚Antwort‘ auf diese Frage wird als ‚Schlussfolgerung‘ präsentiert. Das folgende Bild zeigt die Verteilung der Quantoren für alle Schlusfiguren samt ihren Inversen.

Gesamtübersicht Schlussfiguren 1-3 samt ihren Inversen und die Verteilung der Quantoren für jede Schlussfigur
Gesamtübersicht Schlussfiguren 1-3 samt ihren Inversen und die Verteilung der Quantoren für jede Schlussfigur

9. Man kann in dieser Darstellung schon sehen, dass es im Falle der Schlussfiguren 2 und 3 gar keine Spiegelung vergleichbar zu Figur 1 mit der Figur 4 gibt.

10. Betrachtet man nochmals Figur 1, dann kann man folgende Sachverhalte erkennen (siehe Bild): (i) Bei den Mengenverhältnissen gibt es eigentlich nur drei Fälle (A), (E) = (E-), sowie (A-). Zu jedem dieser drei Fälle für Prämisse 1 kann es dann wiederum kombinatorisch jeweils drei Fälle geben. Spielt man diese durch (das Bild zeigt dies nur für den Fall (A F M) in Prämisse 1), dann zeigt sich (ii) dass von den theoretisch möglichen Fällen 3 x 3 = 9 nur jeweils 3 x 2 = 6 geben kann. Dies ergibt sich daraus, dass eine Kombination von E und E bei dem Muster von Figur 1 zu keinem eindeutigen Schluss führt. Ein Partikularquantor E kann hier immer nur zusammen mit einem Allquantor A auftreten.

Systematik der Mengenverhältnisse am Beispiel von Figur 1
Systematik der Mengenverhältnisse am Beispiel von Figur 1

11. Es fragt sich, wieweit diese Überlegungen auch auf die anderen Schlussfiguren übertragbar sind. Im folgenden Bild sind nochmals alle formal möglichen Quantorenkombinationen für jede Schlussfigur aufgelistet mit der Legende: ‚1‘ := wird von Avicenna genannt, ‚?‘ := unbestimmt, ‚+‘ := würde einen Schluss zulassen:

Syllogismen Figuren 1-3, volle Quantorenverteilung
Syllogismen Figuren 1-3, volle Quantorenverteilung

12. In der Tabelle kann man erkennen, dass es neben den Einsen ‚1‘, die anzeigen, dass diese Quantorenkombinationen in den drei ‚Schlussfiguren Verwendung finden, bei allen Schlussfiguren Fragezeichen ‚?‘ gibt, aber auch Pluszeichen ‚+‘. Dies würde bedeuten, dass es weitere mögliche Schlüsse gäbe, die aber von Avicenna nicht genannt werden.

13. Die Klassifikation ‚?‘ bzw. ‚+‘ habe ich spontan vorgenommen, ‚intuitiv‘. Es fragt sich, ob diese ‚intuitive‘ Zuordnung ‚richtig‘ ist, Eine Antwort auf diese Frage setzt voraus, dass man irgendwelche ‚Kriterien‘ explizit machen kann, anhand deren man die ‚intuitive‘ Klassifikation explizit ‚begründen‘ oder ‚widerlegen‘ kann. Dies soll hier versucht werden.

14. Aus der Geschichte der modernen Logik sind zahlreiche formale Kalküle bekannt, deren ‚Wahrheitsfähigkeit‘
nachgewiesen worden ist. Im vorliegenden Fall wird die Frage aber in einem spezifischen Kontext gestellt: (i) wir setzten hier – versuchsweise — eine allgemeine Bedeutungsfunktion auf der Basis einer dynamischen Objektstruktur voraus und (ii) im Kontext der dynamischen Objektstruktur stellt sich die Frage, wie es möglich ist, ‚zweifelsfrei‘ von zwei vorgegebenen Beziehungen in den Prämissen auf eine dritte Beziehung als Folgerung zu ’schließen‘.

15. Diese Frage hat mindestens zwei Aspekte: (i) einmal, ob und inwieweit wir ‚im Rahmen unseres Bewusstseins‘ Kriterien finden können, die solch eine Unterscheidung unterstützen und (ii) wie die ‚Maschinerie unseres Denkens‘, die dem bewussten Denken vorgelagert ist, diese Aufgabe lösen kann. Dabei fragen wir nicht ‚empirisch‘, ’nicht naturwissenschaftlich‘, sondern ‚logisch, ‚philosophisch‘ in dem Sinne, ob wir überhaupt eine rationale Konstruktion (ein formales Modell) finden können, das eine Erklärung liefern könnte. Dass es dazu dann möglicherweise noch eine empirische Struktur geben könnte, die die Aufgabe ‚anders‘ löst, wäre interessant, würde aber in diesem Kontext dann keine Veränderung bewirken.

16. Es wird notwendig sein, alle 3x 16 Fälle einzeln anzuschauen und zu überprüfen.

17. Darüber hinaus kann man die Frage stellen, ob man die Betrachtung auf andere ‚Typen von wahrheitsfähigen Sachverhalten‘ (auf andere Typen von analytisch wahren Sachverhalten) noch ausweiten kann. Denn die Beispiele mit den Syllogismen der Figuren 1-3(4) sind sehr eng. Und da wir von der modernen formalen Logik wissen, dass man mit den modernen Kalkülen beliebig komplexe Strukturen beschreiben kann, ist die Frage nach weiteren Sachverhalten eigentlich nur eine ‚rhetorische‘ Frage. Allerdings würden wir damit in Richtung einer allgemeinen Logiktheorie steuern. Möglicherweise ist dies hier noch zu früh.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
  • Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
  • Günther Patzig, ‚Die Aristotelische Syllogistik‘, 3. verb.Aufl., Göttingen: Vandenhoeck & Rupprecht, 1969
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 18

Avicenna, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Prädikat, Prämisse, Subjekt, Subjekt - logisches, Syllogismus, Syloogismus - Konjunktiver, Term

(Letzte Änderung 25.Sept.2014, 09:20h)

Die ‚innere Seele‘ der Formen korrespondiert immer mit Klängen. Hier ein weiteres Klangexperiment…… der Klangraum ist unendlich groß …

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Avicennas Übersicht zu Wissen und syllogistischem Denken
Avicennas Übersicht zu Wissen und syllogistischem Denken

1. Nach den vorausgehenden Detailbetrachtungen weitet sich nun der Blick Avicennas auf das Wissen allgemein, und konzentriert sich im Wissen auf das schlussfolgernde Denken in Form von ‚beweisenden Syllogismen‘ (engl.: ‚demonstrative syllogisms‘). Laut Anmerkung des Übersetzers folgt er hier – wie auch in den meisten Teilen zuvor – weitgehend Aristoteles.

2. Avicenna definiert einen (beweisenden) Syllogismus durch die Komponenten (i) Jene Aussagen A1, …, An, die zum Zeitpunkt des Argumentierens als ‚wahr‘ angenommen werden, (ii) Folgerungsregeln, mittels deren man von gegebenen wahren Aussagen auf andere wahre Aussagen ‚mit Notwendigkeit folgern‘ kann, sowie (iii) jene Aussagen F1, …, Fk, die mittels solcher Folgerungsregeln aus den gemachten ‚Annahmen‘ ‚mit Notwendigkeit‘ gefolgert worden sind.

3. [Anmerkung: in einer modernen Schreibweise könnte man einen Syllogismus auch hinschreiben als $latex \{A1, …, An\} \vdash \{F1, …, Fk \}$ gelesen: die Aussagen F1, …, Fk folgen aus den Annahmen A1, …, An mit Hilfe des Folgerungsbegriffs $latex \vdash$ mit Notwendigkeit.]

4. Er unterscheidet dann zwei Arten von Syllogismen: (i) ‚Konjunktive‘ Syllogismen und (ii) ‚Disjunktive‘.

Avicenna - Konjunktiver Syllogismus - Bestandteile
Avicenna – Konjunktiver Syllogismus – Bestandteile

5. Mit der Vorstellung des ‚Konjunktiven Syllogismus‘ führt Avicenna dann – auch hier Aristoteles folgend – eine Reihe von technischen Begriffen ein, um ‚über‘ Syllogismen sprechen zu können.

6. (Konjuktive) Syllogismen bestehen aus drei ‚Aussagen‘, von denen die ersten beiden die ‚Annahmen‘ (‚Prämissen‘) sind, und die dritte die ‚Folgerung‘ (‚Konsequenz‘) aus den vorausgehenden Annahmen.

7. Annahmen wie Folgerungen bestehen jeweils aus drei ‚Ausdrucksteilen‘ A = (A1 A2 A3), von denen er die Ausdrucksteile ‚A2‘ und ‚A3‘ ‚Terme‘ nennt. Der Ausdrucksteil ‚A1‘, bekommt keine eigene Benennung, repräsentiert aber den ‚Quantor‘. Terme können ‚Subjekte S‘ oder ‚Prädikate P‘ sein.

8. Diejenigen Terme in den beiden Annahmen, die in beiden Annahmen gemeinsam sind, nennt er ‚Mittlere Terme‘. Entsprechend nennen wir die beiden anderen, komplementären, Terme hier ‚äußere Terme‘. Den Term in in einer Folgerung, der das Subjekt S repräsentiert und der kein mittlerer Term in einer Annahme ist, nennt er ‚Haupt-Term‘ (‚Major‘). Entsprechend nennt er den Term in einer Folgerung, der das Prädikat P repräsentiert und der kein mittlerer Term ist, den ‚kleinen Term‘ (‚Minor‘). Diejenige Annahme, in der der Haupt-Term der Folgerung vorkommt, wird ‚Neben-Annahme‘ genannt; die andere entsprechend ‚Haupt-Annahme‘.

9. Die typische Aussagestruktur in den Annahmen und in der Folgerung sieht dann so aus: Q (S P). Dabei ist zu beachten, dass Avicenna bei den Syllogismen keine Zeit- und keine Raum-Quantoren benutzt, sondern nur Anzahl-Quantoren, und diese treten nur ‚einfach‘ auf, indem sich der eine Quantor ‚Q‘ in Q(S P) auf die Elemente des Subjekt-Terms S bezieht. Ferner versteht er unter einer ’negativen‘ Aussage nicht die Verneinung der ganzen Aussage – also nicht $latex \neg Q(S\ P)$ –, sondern die Verneinung des Prädikat-Terms P – also $latex Q(S\ \neg P)$ –.

Avicenna Grundstrukturen der drei syllogistischen Schlussfiguren des konjunktiven Syllogismus
Avicenna Grundstrukturen der drei syllogistischen Schlussfiguren des konjunktiven Syllogismus

10. Avicenna stellt dann 3 Muster von Syllogismen vor (siehe Schaubild). Sie sind im wesentlich ’sortiert‘ nach der Verteilung der mittleren bzw. äußeren Terme. Zusätzlich zu den Mustern der mittleren Terme unterscheidet er noch, welche Quantoren die Aussagen haben und ob sie ‚affirmativ‘ oder ’negativ‘ sind.

Tabelle der Quantorenkombinationen relativ zu den Schlußfiguren
Tabelle der Quantorenkombinationen relativ zu den Schlußfiguren

11. Die Tabelle zeigt, welche Quantorenkombinationen Avicenna insgesamt berücksichtigt hat, wie er diese auf die einzelnen Schlußfiguren aufgeteilt hat, und wie ‚asymmetrisch‘ die Verteilung auf die einzelnen Schlußfiguren ausfiel. Auffällig ist, dass Avicenna nicht alle Quantorenkombinationen brücksichtigt, die möglich wären.

Avicennas Schlußfiguren und ein Beispiel für die Quantoren A, A-, E-
Avicennas Schlußfiguren und ein Beispiel für die Quantoren A, A-, E-

12. Am Beispiel der Quantorenkombination (A, A-)E- zeigt das vorausgehende Schaubild, wie unterschiedlich diese Kombination entsprechend den drei Figuren interpretiert wird. Auffällig ist, dass zwei der möglichen Kombinationen für die Schlussfiguren 1 und 2 von Avicenna nicht genutzt werden.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
  • Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15

Analytisch, Art (Spezies), Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - akzidentell, Bedeutung - empirisch, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsraum, Definition, Definition - explitite, Definitorisch, Eigenschaft, Externe Welt, Falsch, Gattung (genus), Kategorien, Kognition, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Logische Operatoren, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt - kontingent, Objekt - universell, Objekthierarchie, Objekttyp, Ontologie, ontologisch, Operator, Operator - aussagenlogischer, Prädikat, Proposition, Sein, Semantik, Subjekt, Subjekt - logisches, Wahr, Wahrheit, Wahrheit - definitorische (analytische), Wahrheit - ontologische, Wahrheit als Übereinstimmung, Wahrheitsbegriff, wahrheitsfähig, Wahrheitsgehalt, Wahrheitskriterium, Wahrheitswert

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M
Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M

WAHR UND FALSCHE AUSSAGEN

1. Nach dem Blogeintrag Avicenna 14b gibt es jetzt Ausdrücke A, B, …, die ‚wahr‘ oder ‚falsch‘ sein können und die wir deshalb ‚Aussagen‘ (auch ‚Propositionen‘) nennen. Aussagen können mittels aussagenlogischer Operatoren wie ‚NEGATION‘, ‚UND‘, ‚IMPLIKATION‘ usw. zu komplexeren Ausdrücken so verknüpft werden, dass jederzeit ermittelt werden kann, wie der Wahrheitswert des komplexen Ausdrucks lautet, wenn die Wahrheitswerte der Teilausdrücke bekannt sind. Ob im Einzelfall eine Aussage A ‚wahr‘ oder ‚falsch‘ ist, muss durch Rückgriff auf ihre Bedeutungsbeziehung M(A) geklärt werden. Bislang ist nur klar, dass die Bedeutungsbeziehung M nur allgemein eine Beziehung zu den (kognitiven) Objekten O herstellt (siehe Grafik oben).

2. Avicenna spricht aber nicht nur von Aussagen A allgemein, sondern unterscheidet die Teilausdrücke ‚Subjekt‘ S und ‚Prädikat‘ P, zusätzlich oft noch ‚Quantoren‘ Q.

FEINSTRUKTUR DER BEDEUTUNG VON AUSDRÜCKEN

3. Man kann und muss dann die Frage stellen, ob und wie sich auf der Bedeutungsseite die Unterscheidung in S und P auf der Ausdrucksseite widerspiegelt?

ECHTE UND UNECHTE OBJEKTE

4. In vorausgehenden Blogeinträgen zu Avicenna (Avicenna 4, 5, 7 und 11) wurde schon unterschieden zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte Objekte‘ sind solche Wissenstatbestände, die man zwar identifizieren und unterscheiden kann, die aber immer nur im Kontext von ‚echten Objekten‘ auftreten. ‚Unechte‘ Objekte werden meistens als ‚Eigenschaften‘ bezeichnet. Beispiel: die Farbe ‚Rot‘ können wir wahrnehmen und z.B. von der Farbe ‚Blau‘ unterscheiden, die Farbe ‚Rot‘ tritt aber nie alleine auf so wie z.B. Gegenstände (Tassen, Stühle, Früchte, Blumen, …) alleine auftreten.

5. Hier wird davon ausgegangen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf.

GATTUNG UND ART; KATEGORIEN

6. Ein Objekt kann viele Eigenschaften umfassen. Wenn es mehr als ein Objekt gibt – also O1, O2, … — die sowohl Eigenschaften Ex gemeinsam haben wie auch Eigenschaften Ey, die unterschiedlich sind, dann kann man sagen, dass alle Objekte, die die Eigenschaften Ex gemeinsam haben, eine ‚Gattung‘ (‚genus‘) bilden, und dass man anhand der ‚unterscheidenden Eigenschaften Ey‘ unterschiedliche ‚Arten‘ (’species‘) innerhalb der Gattung unterscheiden kann.

7. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden.

ONTOLOGISCHE UND DEFINITORISCHE (ANALYTISCHE) WAHRHEIT

8. Bislang ist der Wahrheitsbegriff $latex \top, \bot$ in dieser Diskussion an der hinreichenden Ähnlichkeit eines vorgestellten/ gedachten kognitiven) Objekts $latex a \in Oa$ mit sinnlichen wahrnehmbaren Eigenschaften $latex s \subseteq Os$ festgemacht worden. Ein ‚rein gedachtes Objekt $latex a \in Oa$ ist in diesem Sinne weder ‚wahr‘ $latex \top$ noch ‚falsch‘ $latex \bot$.

9. Setzt man allerdings eine Objekthierarchie O voraus, in der man von einem beliebigen individuellem Objekt a immer sagen kann, zu welchem Objekt Y es als seiner Gattung gehört, dann kann man eine Aussagen der Art bilden ‚a ist eine Tasse‘.

10. Wenn man zuvor in einer Definition vereinbart haben sollte, dass zum Begriff der ‚Tasse‘ wesentlich die Eigenschaften Ex gehören, und das Objekt a hätte die Eigenschaften $latex Ex \cup Ey$, dann würde man sagen, dass die Aussage ‚a ist eine Tasse‘ ‚wahr‘ ist, unabhängig davon, ob es zum kognitiven Objekt a ein ’sinnliches‘ ‚Pendant‘ geben würde oder nicht. Die Aussage ‚a ist eine Tasse‘ wäre dann ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr.

11. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a, die als solche nichts darüber sagt, ob es das Objekt a ‚tatsächlich‘ gibt, soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden, also einer Wahrheit, die sich auf das ‚real Seiende‘ in der umgebenden Welt W bezieht.

12. [Anmerkung: Dieses – auch im Alltagsdenken – unterstellte ‚Sein‘, die unterstellte übergreifende ‚Realität‘ ist nicht nur eine ‚Extrapolation‘ aufgrund sinnlicher Gegebenheiten ‚im‘ wissenden System, sondern ist in seiner unterstellten ‚Realität‘ auch nur eine sehr spezifische Form von Realität. Wie wir heute aufgrund immer komplexerer Messprozeduren wissen, gibt es ‚Realitäten‘, die weit jenseits aller sinnlichen Qualitäten liegen. Es fällt uns nur nicht so auf, weil diese gemessenen Eigenschaften X durch allerlei Prozeduren für unsere Sinnesorgane ‚umgerechnet‘, ‚transformiert‘ werden, so dass wir etwas ‚Sehen‘ oder ‚Hören‘, obgleich das gemessene X nicht zu sehen oder zu hören ist.]

13. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘).

14. Derjenige Ausdrucksteil As, der sich auf das echte Objekt a bezieht, ‚von dem‘ etwas ausgesagt werden soll (‚ist ein…‘, ‚hat …‘), dieser Ausdrucksteil wird als ‚Subjekt‘ S bezeichnet, und der Ausdrucksteil Ap, mittels dem etwas über das Subjekt ausgesagt wird, wird ‚Prädikat‘ P genannt.

15. Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. [Anmerkung: Bei ’neuronalen Netzen‘ wäre das R-Objekt jenes Neuron, das die Verbindung zwischen zwei anderen Neuronen ‚realisiert‘.]

17. Fassen wir zusammen: Bei einem Ausdruck A der Art A=’Hans ist ein Mensch‘ gibt es den Ausdrucksteil As=’Hans‘ und den Ausdrucksteil Ap=’ist ein Mensch‘. Die Bedeutung des Ausdrucksteils As M(As) als M(‚Hans‘) ist ein Objekt h in der unterstellten Bedeutungshierarchie O des Sprechers, das gewisse Eigenschaften E(h) besitzt. Die Bedeutung des Ausdrucksteils Ap als M(Ap) bzw. M(‚ist ein Mensch‘) ist sowohl ein Objekt M mit Eigenschaften E(M) als auch eine Beziehung R_ist zwischen dem Objekt h und dem Objekt M, also R_ist(h,M). Die Beziehung ist definitorisch/ analytisch ‚wahr‘ wenn es gilt, dass die definierenden Eigenschaften E(M) des Objekts Mensch M auch bei den Eigenschaften E(h) von Hans zu finden sind, also $latex E(M) \subset E(h)$ .

BEZIEHUNGSRAUM – TRANSZENDENTALE BEDINGUNGEN

18.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14

Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - empirisch, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Bedeutungsraum, Erfüllung, Falsch, Logik, Logik - Alltag, Logik - Antike, Logische Operatoren, Möglichkeit, Notwendig, Operator, Operator - aussagenlogischer, Semantik, Wahr, Wahrheit, Wissen, Wissen - gefolgertes, Wissen - sensorisches, Wissen - sprachlich vermitteltes, Zutreffen

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

1. Wenn also eine Formulierung von Konvertierungsregeln nicht ohne Bezug auf irgend eine Bedeutung M hinter den Ausdrücken möglich ist, stellt sich zum wiederholten Male die Frage, über welche mögliche Bedeutung M ‚hinter‘ den Ausdrücken gesprochen werden muss.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

2. Beginnen wir mit dem Ausgangspunkt, dass Aussagen PROP solche Ausdrücke von der Menge aller Ausdrücke E sind, die ‚wahr‘ oder ‚falsch‘ sein können. ‚Treffen sie zu‘ gelten sie als ‚wahr‘; ‚treffen sie nicht zu‘ gelten sie als ‚falsch‘.
3. Bislang hatten wir schon die generelle Annahme geäußert, dass das Denken und Wissen eines Menschen im ‚Innern‘ dieses Menschen zu verorten sei und der Mensch ‚in‘ einer umgebenden Welt W mit realen Ereignissen X vorkommt.
4. Um die Begriffe ‚wahr/ falsch‘ bzw. ‚zutreffen/ nicht zutreffen‘ zu ‚erklären‘, nehmen wir an, dass die Menge des möglichen Wissens K eines einzelnen Menschen sich zerlegen lässt in die Teilmengen ‚Vorgestellt‘ K_v, ‚Erinnert‘ K_m sowie ’sinnlich präsent‘ K_s. Es gilt also $latex K = K_{s} \cup M_{v} \cup M_{m}$.
5. Eine Bedeutung wird dann durch eine Beziehung zwischen dem Wissen K und möglichen Ausdrücken $latex PROP \subseteq E$ gebildet: $latex M \subseteq PROP \times K$.
6. Speziell gilt aber, dass man zwischen einer ’neutralen‘ Bedeutung $latex M_n \subseteq E \times (K_{v} \cup K_{m})$ unterscheiden muss, die weder ‚wahr‘ noch ‚falsch‘ ist, und der ’sinnlich fundierten‘ Bedeutung $latex M_s \subseteq E \times K_{s}$. Gibt es zwischen einer neutralen Bedeutung $latex M_{n}$ und einer sinnlich fundierten Bedeutung $latex M_{s}$ eine Beziehung des ‚Zutreffens‘ $latex M_{s} \models M_{n}$, dann kann man sagen, dass das Wissen $latex K_{n}$ in dieser Beziehung ‚wahr‘ ist, andernfalls nicht, geschrieben $latex M_{s} \not\models K_{n}$.
7. Zusätzlich kann man im Bereich des erinnerten Wissens $latex K_{m}$ noch unterscheiden zwischen einem solchen, das Bezug zu ‚vormals sinnlich fundiertem Wissen‘ aufweist als $latex K_{ms}$ und solchem, das ‚keinen Bezug zu vormals fundiertem sinnlichen Wissen‘ aufweist als $latex K_{mns}$.
8. Erinnertes Wissen mit Bezug zu vormals fundiertem Wissen $latex K_{ms}$ hat die Eigenart, dass sich in Abhängigkeit von der ‚Häufigkeit‘ der erinnerbaren Wissenselementen in $latex K_{ms}$ eine Art ‚Erwartung‘ bzgl. des neuerlichen Eintretens dieses Wissens als sinnliches Wissen $latex K_{vs}$ ausbildet: $latex \mu: K_{ms} \longrightarrow K_{vs}$ mit $latex K_{vs} \subseteq K_{v}$, d.h. im Bereich des vorgestellten Wissens $latex K_{v}$ gibt es solches mit einem speziellen Erwartungsanteil $latex K_{vs}$ hervorgerufen durch besondere Erinnerungen.

EXKLUSIVE MODALOPERATOREN

9. An dieser Stelle könnte man dann noch die Begriffe ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ wie folgt einführen: ein vorgestelltes Wissen gilt als ‚möglich‘, wenn der Erwartungswert nicht gleich 1 ist, also $latex \diamond K_{v} \leftrightarrow \mu(K_{v}) \not= 1$, andernfalls als notwendig, also $latex \boxempty K_{v} \leftrightarrow \mu(K_{v}) = 1$
10. Daraus kann man ableiten, dass gelten soll $latex \boxempty K_{v} \leftrightarrow \neg\diamond K_{v}$ oder $latex \neg\boxempty K_{v} \leftrightarrow \diamond K_{v}$.
11. Diese Definition von ‚möglich‘ und ’notwendig‘ entspricht nicht ganz der ‚Intuition‘, dass etwas, was ’notwendig‘ ist, auf jeden Fall auch möglich sein sollte; allerdings folgt – intuitiv — aus der Möglichkeit keine Notwendigkeit. Die vorausgehende Definition von möglich und notwendig erinnert ein wenig an das ‚exklusive Oder‘, das auch ’schärfer‘ ist als das normale Oder. Nennen wie die hier benutzte Definition von ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ daher auch die ‚exklusiven Modaloperatoren‘: Wenn etwas notwendig ist, dann ist es nicht möglich, und wenn etwas möglich ist, dann ist es nicht notwendig.
12. Anmerkung: wenn etwas ‚gedanklich notwendig‘ ist, folgt daraus in diesem Rahmen allerdings nicht, dass es auch tatsächlich sinnlich eintritt. Aus der gedanklichen Notwendigkeit folgt nur, dass es in der erinnerbaren Vergangenheit bislang immer eingetreten ist und daher die Erwartung sehr hoch ist, dass es wieder eintreten wird.

WAHR und FALSCH ABKÜRZUNGEN

13. Wenn man von einer Aussage $latex e \in E$ sagen kann, dass das zugehörige vorstellbare Wissen $latex M(e)=K_{v}$ ‚wahr‘ ist, weil es auf ein sinnliches Wissen $latex K_{s}$ ‚zutrifft oder eben ‚falsch‘, weil es ’nicht zutrifft‘, dann soll dieser Sachverhalt hier wie folgt abgekürzt werden:
14. Eine Aussage A soll genau dann mit ‚wahr‘ $latex \top$ bezeichnet werden, wenn es ein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\top \leftrightarrow M(A)=K_{v}$ und es gibt ein sinnlich fundiertes Wissen $latex K_{s}$, so dass gilt $latex K_{s} \models K_{v}$.
15. Eine Aussage A soll genau dann mit ‚falsch‘ $latex \bot$ bezeichnet werden, wenn es kein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\bot \leftrightarrow M(A)=K_{v}$ und $latex K_{s} \not\models K_{v}$. [Anmerkung: Es gibt nur ein einziges sinnlich fundiertes Wissen, und zwar das jeweils aktuelle!]

AUSSAGEOPERATOREN

16. Jetzt kann man folgende Operatoren über Aussagen definieren:
17. NEGATION: die Verneinung einer Aussage A ist wahr, wenn die Aussage selbst falsch ist, also $latex (\neg A)\top \leftrightarrow (A)\bot$.
18. KONJUNKTION: die Konjunktion $latex \wedge$ von zwei Aussagen A und B ist wahr, wenn beide Aussagen zugleich wahr sind; ansonsten ist die Konjunktion falsch, also $latex (A \wedge B)\top \leftrightarrow (A)\top\ und\ zugleich\ (B)\top$; ansonsten falsch.
19. DISJUNKTION: die Disjunktion $latex \vee$ von zwei Aussagen A und B ist wahr, wenn eine von beiden Aussagen wahr ist; ansonsten ist die Disjunktion falsch, also $latex (A \vee B)\top \leftrightarrow (A)\top\ oder\ (B)\top$; ansonsten falsch.
20. EXKLUSIVE DISJUNKTION: die exklusive Disjunktion $latex \sqcup$ von zwei Aussagen A und B ist wahr, wenn genau eine von beiden Aussagen wahr ist; ansonsten ist die exklusive Disjunktion falsch, also $latex (A \sqcup B)\top \leftrightarrow\ Entweder\ (A)\top\ oder\ (B)\top$; ansonsten falsch.
21. IMPLIKATION: die Implikation $latex \rightarrow$ von zwei Aussagen A und B ist wahr, wenn nicht A wahr ist und zugleich B falsch, also $latex (A \rightarrow B)\top \leftrightarrow\ nicht (A)\top\ und\ zugleich\ (B)\bot$; ansonsten falsch.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13

Allquantor, Avicenna, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Beweis - logischer, Falsch, Folgern - logisches, Konvertierung von Ausdrucksformen, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Partikularquantor, Prädikat, Quantor, Quantor - partikulär, Quantor - universell, Semantik, Subjekt, Wahr, Wahrheit

(Letzte Änderung 8.Sept.2014, 02:59h)

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

AVICENNAS DISKUSSION VON UMWANDLUNG (‚Conversion‘)

1. Aus der englischen Übersetzung ist nicht klar zu entnehmen, ob der Begriff ‚Umwandlung‘ (engl.: ‚conversion‘) tatsächlich eine Form von ‚Umwandlung’/ ‚Umformung’/ ‚Konvertierung‘ meint oder spezieller eine Umformung von Aussagen, die letztlich eine ‚logische Folgerung‘ darstellen. Letztere Interpretation wird angeregt, da er dann tatsächlich an entscheidender Stelle zum ersten Mal in der ganzen Abhandlung eine Folge von Aussagen präsentiert, die man als ‚Folgerungstext‘ interpretieren kann.

2. In seiner Kerndefinition gleich zu Beginn charakterisiert er den Ausdruck ‚Umformung‘ mit Bezug auf zwei Ausdrücke A und B, die Subjekte, Prädikate, Antezedenz und Konsequenz enthalten können (implizit auch Quantoren, da er diese im folgenden Text beständig benutzt). Jede der beiden Aussagen hat eine Bedeutung M(A) bzw. M(B). Umformung hat jetzt damit zu tun, dass einzelne dieser logischen Rollen (Q, S, P, …) ‚ausgetauscht‘ werden, ohne dass dadurch die ‚Bedeutung‘ verändert wird.

3. [Anmerkung: Hier gibt es folgende Unklarheiten: (i) Sollen die Bedeutungen M(A) und M(B) von vornherein ‚gleich‘ sein, und zwar so, dass sie nach dem Austausch unverändert sind? oder (ii) sind die Bedeutungen M(A) und M(B) von vornherein ungleich, sollen aber, jede für sich, auch nach der Umformung gleich sein? In beiden Fällen – so interpretiere ich seine Aussage von Avicenna, gibt es eine Bedeutung vor der Umformung – eine gemeinsame oder eine individuelle –, die nach der Umformung ‚gleich‘ geblieben ist. Schreiben wir für die Umformung als $latex \vdash$, dann würde bedeuten ‚$latex A \vdash B$‘ A wird nach B umgeformt, so dass die Bedeutung von A und B – gemeinsam oder individuell – erhalten bleibt. Es stellt sich hier wieder das Problem – wie im gesamten vorausgehenden Text –, dass der Begriff ‚Bedeutung‘ bei Avicenna nicht scharf definiert ist. Er kann alles und nichts bedeuten. Die ‚Gleichheit‘ von zwei Bedeutungen M_vorher und M_nachher ist also ein ‚offener Begriff‘.]

4. In dem folgenden Text präsentiert Avicenna einerseits einige Beispiele von Umformungen ohne genauere Begründungen, in einem Fall präsentiert er aber das Beispiel einer ausführlicheren Begründung, die wie eine Folgerungstext (wie ein logischer Beweis) aussieht. Beginnen wir mit den Beispielen ohne Begründung.

5. Mögliche Konversion: Von ‚Kein Mensch ist unsterblich‘ ($latex \neg\exists (Mensch)(ist)(unsterblich)$) kann man bedeutungserhaltend umformen in ‚Kein Unsterblicher ist ein Mensch‘ ($latex (\neg\exists (Unsterblicher)(ist)(Mensch)$).

6. Avicenna stellt die Regel auf: Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

7. Beispiel: Von ‚Jeder Mensch ist ein Lebewesen‘ kann ich nicht umformen zu ‚Jedes Lebewesen ist ein Mensch‘ (mehr formalisiert: ($latex \forall (Mensch)(ist)(Lebwesen)$) kann nicht umgeformt werden zu ($latex \forall (Lebewesen)(ist)(Mensch)$).

8. Avicenna stellt die Regel auf: Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

9. Beispiel: Die Aussage ‚Alle F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: Den Ausdruck $latex \forall (F)(sind)(B)$) kann man umformen zu ($latex \exists(B)(ist)(F)$))

10. Avicenna stellt die Regel auf: Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

11. Beispiel: Der Ausdruck ‚Einige F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: ($latex \exists (F)(sind)(B)$) $latex \vdash$ ($latex \exists (B)(sind)(F)$)).

12. Avicenna stellt die Regel auf: Eine negative Partikular-Aussage kann nicht konvertiert werden.

13. Beispiel: Die Aussage ‚Kein Lebewesen ist ein Mensch‘ kann nicht konvertiert werden zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

14. [Anmerkung: Hier gibt es einigen Diskussionsbedarf. Bevor die Diskussion eröffnet wird, hier aber noch das Konvertierungsbeispiel, das wie ein Folgerungstext aussieht.]

15. Ausgangspunkt ist die Regel: Eine negative All-Aussage kann in eine negative All-Aussage konvertiert werden mit dem Beispiel: Von ($latex \neg\exists (Mensch)(ist)(Unsterblicher)$) $latex \vdash$ ($latex \neg\exists (Unsterblicher)(ist)(Mensch)$).

16. Avicenna nennt die nun folgende ‚Folge von Aussagen‘ explizit einen ‚Beweis‘ (engl.: ‚proof‘).

17. Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F). Andernfalls [wäre der Wenn-Dann-Zusammenhang nicht wahr] würde der Widerspruch (engl.: ‚contradictory‘) folgen (Einige B sind F).

18. [Anmerkung: Zur Erinnerung, die Negation einer Implikation (Wenn A dann B) ist nur wahr, wenn A wahr wäre und zugleich B falsch, also ’nicht B‘, d.h. ’nicht(Kein B ist F)‘ d.h. (einige B sind F). Insofern bildet die Aussage (Einige B sind F) einen logischen Widerspruch zu (Kein B ist F). ]

19. Der Beweis beginnt damit, dass Avicenna eine Abkürzung einführt: Er definiert ‚H := ‚Einige B‘. [ein sehr gefährliches Unterfangen…]

20. Dann folgert er ‚H ist gleichbedeutend mit F‘

21. Er folgert weiter: ‚H ist sowohl F als auch B [Damit unterschlägt er, dass H eigentlich nur ‚einige‘ B meinen sollte]

22. Er folgert weiter: Dann gibt es ein F, das auch B ist ($latex \exists (F)(ist)(B)$

23. Er folgert weiter: Nehme ich die Aussage (Einige B sind F) als wahr an, dann komme ich zu der Aussage (Einige F sind B); dies steht aber im Widerspruch zu der Ausgangsbehauptung, das ‚Kein F ist B‘.

24. Er folgert weiter: Deshalb ist es nicht möglich, von der Ausgangsbehauptung ‚Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F)‘ auf den Widerspruch ‚Einige F sind B‘ zu schließen.

25. Avicenna folgert weiter: Von daher, wenn es gilt, dass ‚Kein F ist B‘, dann gilt auch die Konvertierung ‚Kein B ist F‘.

DISKUSSION

KONVERTIERBARKEIT DER FORMEN (Q (A B)) zu (Q (B A)) – BEDEUTUNGSABHÄNGIG

26. In den Beispielen, die Avicenna präsentiert, gibt es zwei Beispiele, die verwirrend sind. Im einen Fall will er über ’negative All-Aussagen‘ ($latex \neg\forall$) sprechen und im anderen Fall über ’negative Partikular-Aussagen‘ ($latex \neg\exists$). Das Beispiel für negative All-Aussagen lautet ‚Kein Mensch ist unsterblich‘. Der Quantor ‚kein‘ ist aber definiert als ’nicht einige‘ bzw. ‚$latex \neg\exists$‘. Dies aber ist gleichbedeutend mit einer negativen Partikular-Aussage. Später präsentiert er als Beispiel für negative Partikular-Aussagen den Ausdruck ‚Kein Lebewesen ist ein Mensch‘ ($latex \neg\exists (Lebewesen)(ist)(Mensch)$).

27. Damit haben wir es mit folgenden Widersprüchlichkeiten zu tun: (i) Avicenna interpretiert seinen Begriff der negativen Allaussagen mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert; (ii) Mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert, argumentiert er, dass man bedeutungserhaltend negative All-Aussagen konvertieren kann; (iii) Mit einem anderen Beispiel einer negativen Partikularaussage argumentiert er, man könne dieses nicht konvertieren.

28. Da das Beispiel zu (ii) zeigt, dass man sehr wohl eine negative Partikular-Aussage konvertieren kann, fragt man sich, warum es in einem anderen Fall nicht gehen soll. Dazu kommt, dass das konkrete Beispiel, das Avicenna präsentiert, aus sich heraus fragwürdig erscheint: ‚Kein Lebewesen ist ein Mensch‘ soll nicht konvertierbar sein zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

29. Bekannt ist – zumindest bezogen auf diese Begriffe –, dass sehr wohl einige Lebewesen Menschen sind, also eher gilt $latex \neg\neg\exists (Lebewesen)(ist)(Mensch)$, d.h. $latex \exists (Lebewesen)(ist)(Mensch)$. Von einer Aussage wie $latex \neg\exists (Mensch)(ist)\neg(Lebewesen)$) könnte man allerdings nicht konvertieren zu $latex \neg\exists (Lebewesen)(ist)\neg(Mensch)$).

30. Trotzdem gibt es eine mögliche Konvertierung von ($latex \neg\exists (Mensch)(ist)(Unsterblich)$)) zu ($latex \neg\exists (Unsterblich)(ist)(Mensch)$)).

31. Diese Beispiele legen die Vermutung nahe, dass die bisherigen ‚Konvertierungsregeln‘ von Avicenna nicht unabhängig sind von der jeweils unterstellten Bedeutung der beteiligten Subjekte und Prädikate.

32. Bezogen auf die Struktur (Q (A B)) $latex \vdash (Q (B A))$ hängt die Möglichkeit oder Unmöglichkeit einer Konvertierung in den Beispielen davon ab, wie sich die Bedeutungen von A und B, also M(A) und M(B), zueinander verhalten.

33. Zwei Hauptfälle kann man unterscheiden: (i) die Bedeutung von beiden Ausdrücken ist ‚gleich‘, d.h. M(A) = M(B), oder (ii) die Bedeutungen sind ungleich in dem Sinne, dass zwar alle Elemente, die zu M(B) gehören auch in M(A) sind, aber nicht umgekehrt, also $latex M(B) \subseteq M(A)$.

34. Wenn wir Fall (i) M(A) = M(B) unterstellen können, dann kann man von $latex \forall A sind B$ auf $latex \forall B sind A$ schließen, oder $latex \exists A sind B$ und umgekehrt. Die Aussage $latex \neg\forall A sind B$ wäre formal zwar möglich, wäre aber ’semantisch‘ (aufgrund der angenommenen Bedeutung) aber nicht möglich. Genau sowenig wie $latex \neg\exists A sind B$ semantisch möglich wäre, wohl aber syntaktisch.

35. Unterstellen wir hingegen den Fall (ii) $latex M(B) \subseteq M(A)$, dann würde die Konvertierung von $latex \forall A sind B$ auf $latex \forall B sind A$ nicht gelten. Entsprechend kann man die wahre Aussage $latex \forall B sind A$ nicht konvertieren zu $latex \forall A sind B$. Die Konvertierung $latex \exists A sind B$ würde gehen wie auch umgekehrt. Die Aussage $latex \neg\forall A sind B$ ist wahr, die Konvertierung zu $latex \neg\forall B sind A$ wäre falsch. Usw.

36. Diese Beispiele verdeutlichen, dass die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) zu (Q (B A)) eindeutig von der angenommenen Bedeutungsstruktur abhängig ist (zumindest in dem Kontext, den Avicenna diskutiert). Betrachten wir seine anderen Konvertierungsregeln.

37. (i) Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

38. (ii) Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

39. (iii) Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

40. (iv) Eine negative Partikular-Aussage kann nicht konvertiert werden.

41. Zu (i): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel nicht.

42. Zu (ii) und (iii): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel auch.

43. Zu (iv): Dieser Fall ist von der Form her (rein syntaktisch) möglich, von der Bedeutung her (rein semantisch) aber ausgeschlossen.

44. Bei allen bisherigen Konvertierungsbeispiele von Avicenna ist zu beachten, dass sich die Bedeutung des Subjekts S und des Prädikats P in einer Aussage (S P) in der Art $latex M(A) = M(B)$ oder $latex M(B) \subseteq M(A)$ beschreiben lässt. Dies setzt voraus, dass sich ein Prädikat P auch als eine Menge von Objekten auffassen lässt, denen eine bestimmte Eigenschaft E zukommt, also etwa P := ‚eine Menge von Elementen, die die Eigenschaft P haben‘. Zu sagen ‚S ist P‘ würde dann sagen, dass die Elemente die S sind auch die Elemente sind, die P sind.

45. Man muss hier die Frage stellen, ob Prädikate immer diese Form haben.

KONVERTIERUNG OHNE BEDEUTUNG?

46. Macht man die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) und (Q (B A)) von der Bedeutung M der Ausdrücke A und B abhängig, dann hängt die Formulierung der Konvertierungsregeln ab von einer brauchbaren Definition des zugrundeliegenden Bedeutungsraumes samt seiner Interaktion mit den Ausdrucksformen. Im weiteren Verlauf soll dies explizit untersucht werden. Es stellt sich aber auch die Frage, ob man Konvertierungsregeln nicht auch ohne Rückgriff auf die Bedeutung der Teilausdrücke formulieren kann.

47. Hat man nur die Ausdrücke (Q (S P)) mit der Verallgemeinerung, dass S und P ‚gleichwertig‘ sein können im Sinne von (Q (A B)) $latex \vdash$ (Q (B A)), dann stellt sich die Frage welche Kriterien man hätte, gäbe es keinen Bedeutungsbezug?

48. Man muss feststellen, dass ohne irgendeinen Bedeutungsbezug die Ausdrücke als solche keinerlei Ansatzpunkt bieten, eine Konvertierung zuzulassen oder sie zu verbieten.

49. Wenn aber Konvertierungsregeln ohne Bedeutung keinen Sinn machen, dann muss man sich fragen, welche Bedeutungsstrukturen man benötigt, dass man solche Konvertierungsregeln sinnvoll einführen kann.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

50. Wenn es also ohne Bezug auf eine Bedeutung nicht geht, stellt sich die Frage, wie eine solche Bedeutungsstruktur aussehen muss, damit solche – oder auch andere – Konvertierungsregeln formuliert werden können.

51. Die weitere Diskussion wird in einem neuen Blogeintrag fortgeführt werden.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.