Journal: Philosophie Jetzt – Menschenbild, ISSN 2365-5062, 20.Sept. 2018
URL: cognitiveagent.org
Email: info@cognitiveagent.org
Autor: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
KONTEXT
Die Diskussion im Kontext des letzten Textes von Freud zur Psychoanalyse lässt erkennen, wie sich das Bild von uns Menschen über uns selbst dadurch in gewisser Weise ändern kann und letztlich dann ändert, wenn wir uns auf diese Gedanken einlassen. Die Einbeziehung des ‚Unbewussten‘ in das Gesamtbild des Systems homo sapiens verschiebt so manche Beziehungen im Gefüge des menschlichen Selbstbildes, und nicht nur das, es wirkt sich auch aus auf das Gesamtbild der empirischen Wissenschaften, auf ihr Gesamtgefüge. Dies hatte sich ja auch schon angedeutet in der vorausgehenden Diskussion des Buches von Edelman, die noch nicht abgeschlossen ist.
Dies hat mich angeregt, über Freud und Edelman hinausgehenden einige der epistemischen Schockwellen zusammen zu stellen, denen das menschliche Selbstverständnis in den letzten ca. 3500 Jahren ausgesetzt war. Dabei muss man sich darüber im Klaren sein, dass es natürlich immer nur eine Minderheit war, die überhaupt an den übergreifenden Erkenntnissen teilhaben konnte, und selbst diese Minderheit zerfällt in unterschiedliche Subgruppen ohne ein kohärentes Gesamtbild.
EPISTEMISCHE SCHOCKWELLEN
Unter ‚Schockwellen‘ werden hier energetische Ereignisse verstanden, die nur gelegentlich auftreten, und die geeignet sind, bestehende Strukturen zumindest zum Schwingen, zum Erbeben zu bringen, wenn nicht gar zu ihrer Zerstörung führen. ‚Epistemisch‘ bezieht sich auf die Dimension des Erkennens, des Verstehens, zu dem Exemplare des Homo sapiens fähig sind. ‚Epistemische Schockwellen‘ sind also Ereignisse, durch die das Selbstverständnis, die Weltbilder der Menschen in Schwingungen versetzt wurden bzw. sich neu aufbauen mussten.
Die folgende Zusammenschau solcher epistemischer Schockwellen ist in keiner Weise vollständig, weitgehend nicht differenziert genug, rechtfertigt sich aber dadurch, dass es darum geht in einer überschaubaren Weise einen Grundeindruck von der Dynamik des Geistes zu vermitteln, die dem Geschehen des biologisch fundierten Lebens innewohnt.
CLUSTER RELIGION

Zwischen ca. -1500 bis etwa 650 gab mindestens 8 große das Weltverstehen prägende Ereignisse – daneben viele andere, weitere –, die wir im Nachgang als ‚Religionen‘ bezeichnen. Religionen zeichnen sich aus durch ‚Gründer‘, durch ‚Botschaften‘, durch ‚Erfahrungen‘ und dann meistens nachfolgend durch ‚Regeln‘ und Bildung von ‚Organisationsformen‘. Sie erheben einen Anspruch auf ‚Deutung der Welt‘ mit ‚Sinn‘, ‚Werten‘ und ‚Spielregeln‘. Sie versprechen auch den Kontakt zu eine Letzten, Größten, Umfassenden, Endgültigen, dem alles andere unter zu ordnen ist. Vielfach gehen diese Versprechungen auch einher mit speziellen ‚außergewöhnlichen Erlebnissen‘, die im einzelnen stattfinden.
In Vorderasien und Europa waren dies vor allem das Duo Judentum-Christentum und der Islam. Während diese sich explizit auf einen ‚Schöpfer‘ bezogen, kam der indische Subkontinent neben der vielfältigen Götterwelt des Hinduismus in seinem Grundtenor — realisiert im Buddhismus — ohne einen expliziten Schöpfer aus, allerdings nicht ohne eine tiefgreifende Existenzerfahrung des einzelnen Menschen, der sich durch einen geeigneten Lebensstil und Meditation möglichst weitgehend von einem normalen Alltag und seinen vielfältigen Spannungen isolierte.
So verschieden Jugentum-Christentum, Islam auf der einen Seite und Indischer Existentialismus auf der anderen Seite auf den ersten Blick wirken können, kann man aber dennoch auffällige strukturelle Parallelen erkennen.
Die sprachliche Seite der genannten Religionen tendiert dazu, nicht die Weite und Vielfalt der Welt zu kommunizieren, keine weiterreichende Erkenntnisse, sondern die Sprache hat einzig den Zweck, eine bestimmte, abgegrenzte Idee zu kommunizieren, diese abzugrenzen von allem anderen, bis dahin, dass alle Abweichungen diskreditiert werden. Jene Menschen, die sich sprachlich von der ‚Norm‘ entfernen sind Abweichler, Dissidenten, Ungläubige, Verräter, Feinde. Die Sprache wird also nicht gesehen als ein offener, lebendiger, dynamischer Raum von ‚Wahrheit‘, die sich weiter entwickeln kann, sondern als eine symbolische Fessel, eine symbolische Mauer, die einige wenige Ideen abgrenzen sollen. Auch der Buddhismus, der eigentlich sein Fundament in einer schwer beschreibbaren individuellen Existenzerfahrung sieht, praktiziert Sprache überwiegend als Gefängnis.
Betrachtet man sich die Geschichte dieser Religionen bis heute, dann ist diese Starrheit unübersehbar. Alle modernen Erkenntnisse und Entwicklungen prallen an der Sprache dieser Religionen ab.
Neben der sprachlichen Dimension haben alle diese Religionen auch eine ‚Erlebnisdimension‘, oft auch ‚Spiritualität‘ oder ‚Mystik‘ genannt. Einzelne, Gruppierungen, Bewegungen erzähltem davon, schrieben es auf, dass sie ‚besondere, tiefgreifende Erlebnisse‘ hatten, die ihnen ‚klar gemacht haben‘, was wirklich ‚wichtig‘ ist, ‚worin der Sinn des Lebens‘ liegt, Erlebnisse, die ihnen ‚Frieden‘ geschenkt haben, ‚Erfüllung‘, ‚Wahrheit‘. Und diese Erlebnisse waren immer so stark, dass sie diese Menschen aus allen Schichten dazu bewegt haben, ihr Lebens radikal zu ändern und von da an eben ‚erleuchtet‘ zu leben. Diese Menschen gab es nicht nur im Umfeld des Buddhismus, sondern auch zu Tausenden, Zehntausenden im Umfeld des Judentum-Christentums.
Solange diese religiösen Bewegungen sich im Umfeld der etablierten religiösen Überzeugungen und Praktiken bewegen wollten, mussten sie sich – wie immer auch ihre individuellen Erlebnisse waren – diesem Umfeld anpassen. In vielen Fällen führte dies auch zu Absetzbewegungen, zur Entwicklung neuer religiöser Bewegungen. Das Problem dieser erlebnisbasierten Bewegungen war, dass sie entweder nicht die Sprache benutzen durften, die sie zur Beschreibung ihrer Erlebnisse brauchten (da nicht erlaubt), oder aber, sie benutzten eine neue Sprache, und dies führte zum Konflikt mit den etablierten Sprachspielen.
Unter den vielen hunderten Bewegungen allein im Bereich Judentum-Christentum, die z.T. viele tausend, ja zehntausend Mitglieder hatten und dabei oft auch materiell sehr wohlhabend bis reich wurden, möchte ich zwei kurz erwähnen: die Reformation angefeuert von Martin Luther und den Jesuitenorden, angefeuert von Ignatius von Loyola. Im historischen Klischee werden beide Bewegungen oft als direkte Gegner skizziert, da der Jesuitenorden kurz nach Beginn der Reformationsbewegung gegründet wurde und der katholische Papst gerade diesen Orden auch zur ‚Bekämpfung der Reformation‘ einsetzte. Dieses Bild verdeckt aber die wirklich interessanten Sachverhalte.
Der Jesuitenorden entstand aus den spirituellen Erfahrungen eines baskischen Adligen, deren innere Logik, Beschreibung und Praxis, im Lichte der Erkenntnisse der modernen Psychologie (und Psychoanalyse) stand halten würde. Außerdem war der Orden aufgrund dieser Spiritualität extrem weltoffen, wissenschaftsaffin, und revolutionierte die damals beginnende christliche Missionierung der Welt, indem jeweils die Kultur der verschiedenen Erdteile studiert und übernommen und sogar gegen zerstörerische Praktiken der europäischen Kolonisatoren geschützt wurden. Genau dieses wahre Gesicht des Ordens mit einer radikal individuell-erlebnisbasierten Spiritualität und daraus resultierenden Weltoffenheit und Menschlichkeit führte dann zum Verbot und Aufhebung des Ordens weltweit, verbunden mit Einkerkerungen, Folter und Tod ohne Vorankündigung. Das korrupte Papsttum ließ sich damals von dem portugiesischen und spanischen Hof erpressen, die ihre menschenverachtende Geschäfte in den Kolonien, speziell Südamerika, bedroht sahen. Dies war nicht die einzige Aufhebung und Misshandlung, die der Orden seitens des Papstums erfuhr. Während Luther sich gegen das Papsttum erhob und es auf einen Konflikt ankommen ließ, blieben die Jesuiten dem Papst treu und wurden vernichtet.
Diese Minigeschichte ließe sich aber zu einem großen Thema erweitern, da eben die sprachlich fixierten Religionen generell ein Problem mit Wahrheit und damit mit jeglicher Art von Erfahrung haben. Die Akzeptanz individueller Erfahrung als möglicher Quell von ‚Wahrheit‘, möglicherweise einer weiter reichenden alternativen Wahrheit zu der sprachlich fixierten (und damit eingesperrten) Wahrheit der Religionen, eine solche Akzeptanz würde das Wahrheitsmonopol dieser Religionen aufheben. Bislang hat keine der genannten Religionen es geschafft, von sich aus ihr problematisches Wahrheitsmonopol in Frage zu stellen.
JUDENTUM – CHRISTENTUM – PHILOSOPHIE
In der Zeit vor den modernen empirischen Wissenschaften existierte wissenschaftliches Denken entweder gar nicht oder in enger Verbindung mit dem philosophischen Denken bzw. der Medizin.
In der alten und klassischen Griechischen Philosopie (ca. -800 bis -200) wurde das Weltverstehen in vielen Bereichen erstmalig sehr grundlegend reflektiert, unabhängig von bestimmten religiösen Überzeugungen, obgleich natürlich auch diese Denker nicht im luftleeren Raum lebten sondern in konkreten Kulturen mit einer damals üblichen Moral, Ethik, Spielregeln, Sprachspielen.
Unter den vielen bedeutenden Konzepten war das größte systematische Konzept wohl jenes von Aristoteles, Schüler Platons, und den an ihn anschließenden Schulen. Während dieses griechische Denken nach der Eroberung Griechenlands durch die Römer in Mittel- und Westeuropa bis zum Jahr 1000 mehr oder weniger unbekannt war (Kriege, radikal anti-wissenschaftliche Einstellung der katholischen Kirche) war der damalige Islam sehr offen für Wissen. Das griechische Denken war im Islam weitgehend bekannt, lag entsprechend in arabischen Übersetzungen vor, und durch eine Vielzahl von Schulen, Bildungsstätten und großen Bibliotheken (z.T. mehrere hundert Tausend Bücher!) wurde dieses Wissen gepflegt und weiter entwickelt (welcher Kontrast zum heutigen Islam!). Und nur über diese Umweg über den hochgebildeten Islam mit Übersetzungsschulen in Spanien kam das Wissen der Griechen ab ca. 1000 wieder in das christliche Mittel- und West-Europa.
Mit dem Entstehen eines aufgeschlosseneren Bildungssystem in Europa wanderten die griechischen Gedanken über Bücher und Gelehrte wieder in europäische Bildungsstätten ein. Es gab eine Zeit der intensiven Auseinandersetzung zwischen bisheriger christlicher Theologie und Aristoteles. Auf dem Höhepunkt der begrifflichen Integration von christlichem Glauben und Aristotelischer Weltsicht gab es aber ‚Abspaltungstendenzen‘ in mehreren Bereichen.
POLITIK – WISSENSCHAFT – SPIRITUALITÄT
Das zunehmend freie und kritische Denken begann mit der Infragestellung der bis dahin waltenden absolutistischen Machtstrukturen.
Das methodisch geschulte universitäre Denken begann, über die aristotelischen Konzepte hinaus zu denken. Anknüpfungspunkte gab es genügend.
Das individuelle Erleben der Menschen, ihre Frömmigkeit, ihre Spiritualität suchte nach neuen Wegen, benutzte eine neue Sprache, um sich besser ausdrücken zu können.
Das neue politische Denken führte später zur französischen Revolution und vielen ähnlichen politischen Erneuerungsbewegungen.
Das neue philosophische Denken führt alsbald zum Bildung der neuen empirischen Wissenschaften mit neuer Logik und Mathematik.
Die neue Spiritualität lies viele neue religiöse Bewegungen entstehen, die quer zu allen etablierten Glaubensformen lagen, u.a. auch zur Reformation.
PHILOSOPHIE – WISSENSCHAFT

Aus der Vielzahl der philosophischen Denker bieten sich vier besonders an: Descartes, Kant, Wittgenstein und Carnap.
Von heute aus betrachtet markieren diese Vier entscheidende Umbrüche des philosophischen Denkens, das von den Entwicklungen in der Logik, Mathematik,Physik, Geowissenschaften, Biologie und Psychologie zusätzlich profitiert hat und noch immer profitiert.
Descartes versuchte zu klären, inwieweit sich die Wahrheitsfrage nur durch Rekurs auf das eigene Denken lösen ließe. Sein Fixpunkt in der Gewissheit des eigenen Denkens (cogito ergo sum) wurde aber erkauft durch einen fortbestehenden Dualismus zwischen Körper (res extensa) und Denken/ Geist (res cogitans), den er mit einem irrationalen Gedanken zu einer Zirbeldrüse zu kitten versuchte.
Kant führte dieses Forschungsprogramm von Descartes letztlich weiter. Sein Vermittlungsversuch zwischen fehlbarer konkreter empirischer Erfahrung und den allgemeinen Prinzipien der Mathematik und des Denkens (des Geistes) ging über Descartes insoweit hinaus, dass er auf eine Zirbeldrüsen-ähnliche Lösung verzichtete und stattdessen davon ausging, dass der Mensch in seinem Denken von vornherein in abstrakten Kategorien wahrnimmt und denkt. Unsere menschliche Konstitution ist so, dass wir so wahrnehmen und Denken. Er konstatierte damit ein Faktum, das wir heute mit all unseren Erkenntnissen nur bestätigen können. Es blieb bei ihm offen, warum dies so ist. Es zeichnet seine intellektuelle Redlichkeit aus, dass er die offenen Enden seiner erkenntnistheoretischen (epistemischen) Analysen nicht krampfhaft mit irgendwelchen Pseudo-Lösungen versucht hat zu vertuschen.
Wittgenstein war der erste, der sich mit dem Funktionieren der Sprache und ihrer Wechselwirkung mit unserem Denken ernsthaft, ja radikal beschäftigte. Während er in seinem Frühwerk noch der Statik der damaligen modernen Logik huldigte, begann er dann später alle diese statischen formalen Konstruktionen in der Luft zu zerreißen, durchlief weh-tuende detaillierte Analysen der Alltagssprache, machte vor nichts Halt, und hinterließ mit seinem frechen und angstfreien Denken einen Trümmerhaufen, dessen Verdienst es ist, den Raum frei gemacht zu haben für einen echten Neuanfang.
Carnap wirkt in diesem Zusammenhang auf den ersten Blick wie ein Antipode zu Wittgenstein, und in der Tat hat er ja das vor-wittgensteinsche Sprachverständnis in seinen Studien zu den formalen Sprachen, zur Logik, zur logischen Semantik weiter angewendet. Allerdings hat er dies dann auch im Kontext der empirischen Wissenschaften getan. Und in diesem Kontext hat sein formal-scholastisches Denken immerhin dazu beigetragen, die Grundstrukturen moderner empirische Theorien mit einem formalen Kern frei zu legen und ihre Eigenschaften zu untersuchen.
Alle diese genannten Ansätze (Kant, Wittgenstein, Carnap) wurden später mehrfach kritisiert, abgewandelt, weiter entwickelt, aber es waren diese Ansätze, die die nachfolgenden Richtungen entscheidend beeinflusst haben.
Ein interessanter Grenzfall ist Freud (s.u.). Irgendwie könnte man ihn auch zur Philosophie rechnen.
LOGIK – MATHEMATIK
Aus heutiger Sicht kann man sich gar nicht mehr vorstellen, dass es eine Zeit gegeben hat, in der die moderne Logik und Mathematik nicht verfügbar war. Nahezu alles, was unseren Alltag ausmacht setzt sehr viel Mathematik als beschreibende Sprache, als Berechnung, als Simulation voraus. Dass mathematisches Denken in den Schulen so wenig – und immer weniger – behandelt wird, ist sehr irritierend.
Logik und Mathematik sind einen weiten Weg gegangen.
Ein Meilenstein ist der Übergang von der klassischen aristotelischen Logik (eng an der Alltagssprache, Einbeziehung inhaltlichen Alltagsdenkens) zur modernen formalen Logik seit Frege (formale Sprache, formaler Folgerungsbegriff).
Eng verknüpft mit der Entwicklung der neuen formalen Logik ist auch die Entwicklung der modernen Mathematik, die entscheidend mit der Erfindung der Mengenlehre durch Cantor ihren Durchbruch fand, und dann mit Russel-Whitehead und Hilbert die Neuzeit erreichte. Keine der modernen Arbeiten in Gebieten wie z.B. Algebra, Topologie, Geometrie sind ohne diese Arbeiten denkbar, ganz zu schweigen von der modernen theoretischen Physik.
EMPIRISCHE WISSENSCHAFTEN
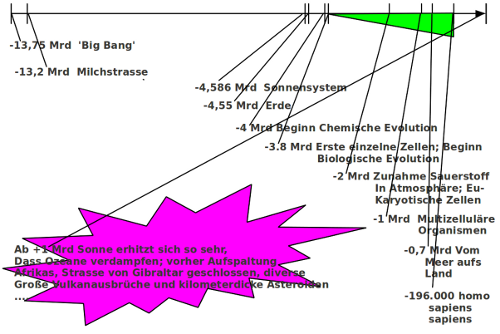
Erste Ausläufer empirischer Wissenschaft gab es schon vor Galilei (man denke z.B. nur an die bahnbrechenden Forschungen zur Medizin von dem islamischen Gelehrten (und Philosophen, Logiker, Theologen!) Avicenna). Doch an der Person Galileis kristallisiert sich der Konflikt zwischen neuem, offenen wissenschaftlichen Denken und dem alten, geschlossenen christlichen Denken. Zudem hat Galilei eben konsequent sowohl eine experimentelle Messmethode angewendet wie auch eine beginnende mathematische Beschreibung. Mit Newton gelang dann eine Fassung von Experiment und Theorie, die atemberaubend war: die Bewegung der Himmelskörper ließ sich nicht nur mit einfachen mathematischen Formeln beschreiben, sondern auch noch mit bis dahin unbekannter Präzision voraus sagen. Es sollte dann zwar noch fast 300 Jahre dauern, bis die moderne Physik eine erste Theorie zur Entstehung des ganzen Weltalls formulieren konnte samt ersten experimentellen Bestätigungen, aber die Befreiung des Denkens von dogmatischen Sprachbarrieren war geschafft. Die Wissenschaft insgesamt hatte sich freigeschwommen.
Schon im 17.Jahrhundert hatte Niels Stensen entdeckt, dass die unterschiedlichen Ablagerungsschichten der Erde in zeitlicher Abfolge zu interpretieren sind und man daher auf geologische Prozesse schließen kann, die die Erde durchlaufen haben muss.
Zwei Jahrhunderte später, schon im 19.Jahrhundert, wurde diese historische Sicht der Erde ergänzt durch Charles Darwin, der am Beispiel der Pflanzen- und Tierwelt auch Hinweise auf eine Entwicklung der Lebensformen fand. Sowohl die Erde als auch die biologischen Lebensformen haben eine Entwicklung durchlaufen, zudem in enger Wechselwirkung.
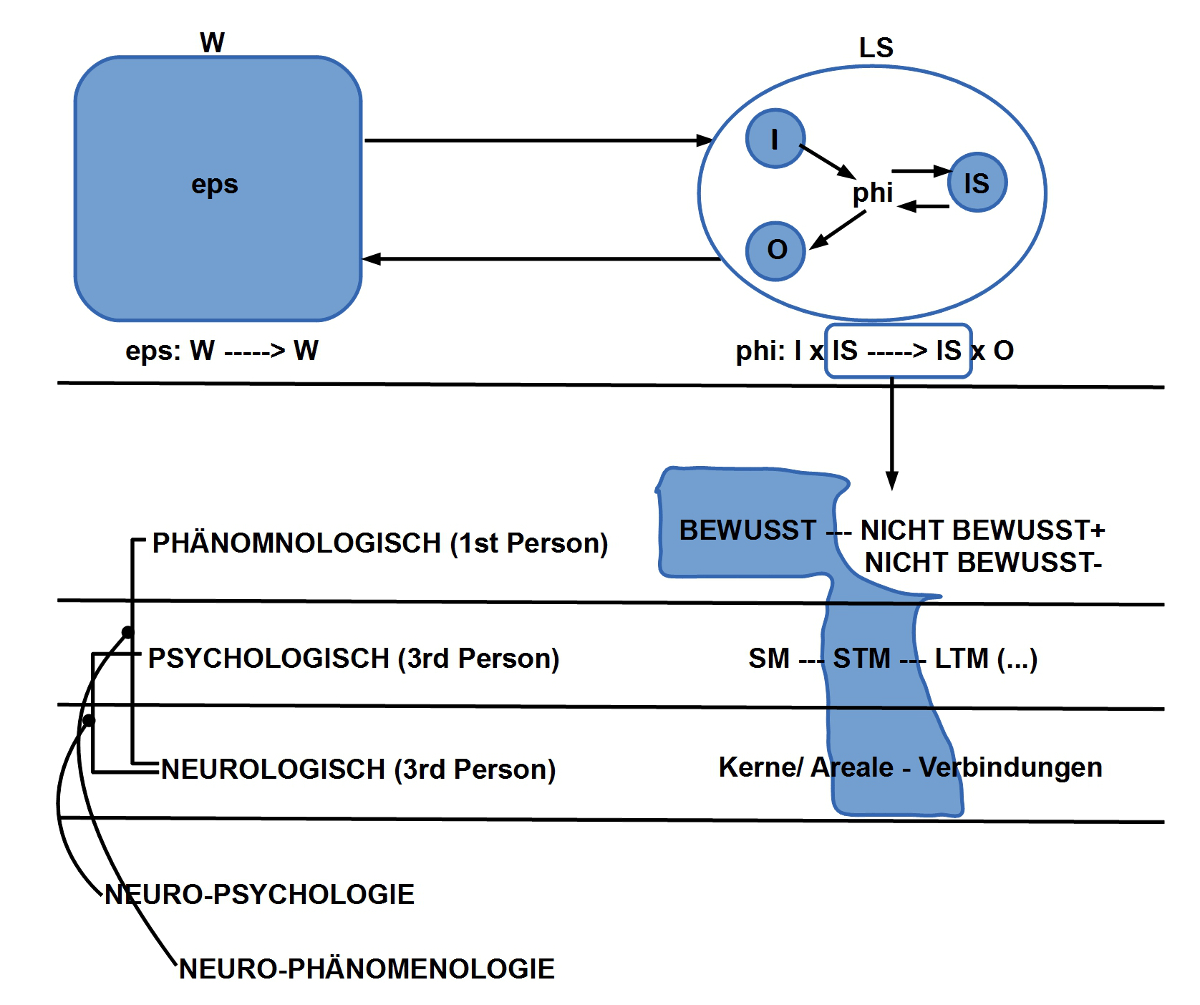
Fast parallel zu Darwin machte Freud darauf aufmerksam, dass unser ‚Bewusstsein‘ nicht die volle Geschichte ist. Der viel größere Anteil unseres menschlichen Systems ist ’nicht bewusst‘, also ‚unbewusst‘. Das Bewusstsein ‚erzählt‘ uns nur ‚Bruchstücke‘ jener Geschichten, die weitgehend im ‚Nicht-Bewusstein‘ oder ‚Unbewussten‘ ablaufen.
Die weitere Entwicklung der Biologie lieferte viele Argumente, die das Bild von Freud stützen.
Der Versuch von Watson, 1913, die Psychologie als empirische Verhaltenswissenschaft zu begründen, wurde und wird oft als Gegensatz zu Psychoanalyse gesehen. Das muss aber nicht der Fall sein. Mit der Verhaltensorientierung gelang der Psychologie seither viele beeindruckende theoretische Modelle und Erklärungsleistungen.
Von heute aus gesehen, müsste man ein Biologie – Psychologie – Psychoanalyse Cluster befürworten, das sich gegenseitig die Bälle zuspielt.
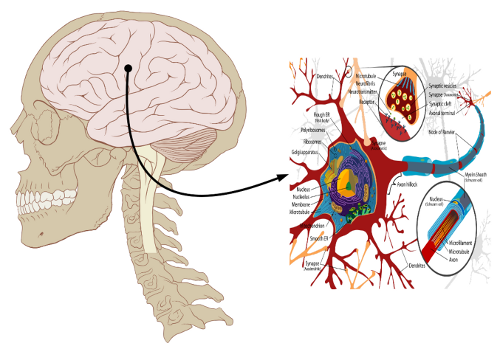
Durch die Einbeziehung der Mikro- und Molekularbiologie in die Evolutionsbiologie konnten die molekularen Mechanismen der Evolution entschlüsselt werden.Mittlerweile steht ein fast komplettes Modell der biologischen Entwicklung zur Verfügung. Dies erlaubt es sowohl, Kants (als auch Descartes) Überlegungen von den biologischen Voraussetzungen her aufzuklären (z.B. Edelman!), wie auch die Psychologie samt der Psychoanalyse.
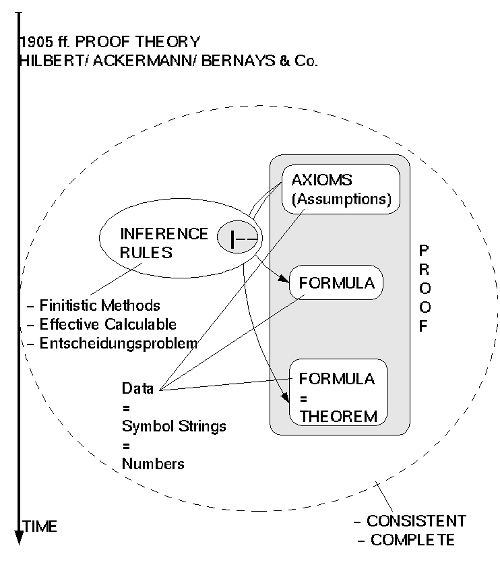
COMPUTER
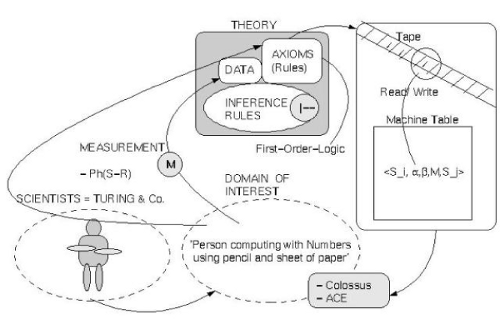
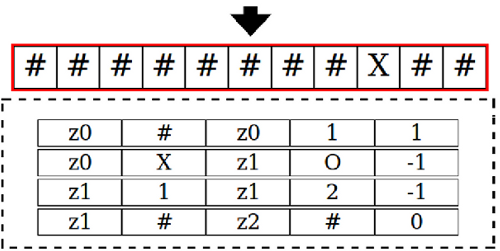
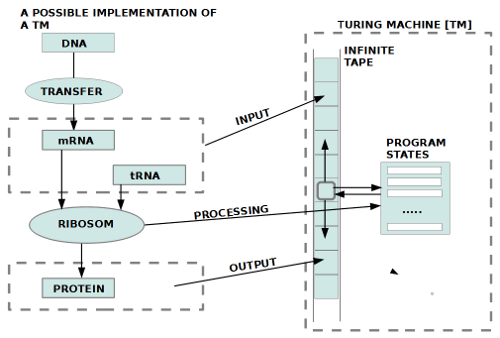
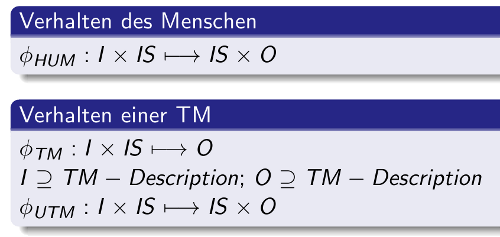
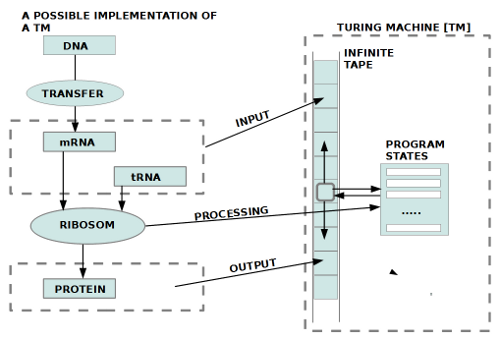
Als Gödel 1931 die Unentscheidbarkeit anspruchsvoller mathematischer Theorien (das fängt bei der Arithmetik an!) beweisen konnte, wirkte dies auf den ersten Blick negativ. Um seinen Beweis führen zu können, benötigte Gödel aber sogenannte ‚endliche Mittel‘. Die moderne Logik hatte dazu ein eigenes Forschungsprogramm entwickelt, was denn ‚endliche Beweismethoden‘ sein könnten. Als Turing 1936/7 den Beweis von Gödel mit dem mathematischen Konzept eines Büroangestellten wiederholte, entpuppte sich dieses mathematische Konzept später als ein Standardfall für ‚endliche Mittel‘. Turings ‚mathematisches Konzept eines Büroangestellten‘ begründete dann die spätere moderne Automatentheorie samt Theorie der formalen Sprachen, die das Rückgrat der modernen Informatik bildet. Das ‚mathematische Konzept eines Büroangestellten‘ von Turing wurde ihm zu Ehren später ‚Turingmaschine‘ genannt und bildet bis heute den Standardfall für das, was mathematisch ein möglicher Computer berechnen kann bzw. nicht kann.
Im weiteren Verlauf zeigte sich, dass gerade das Konzept des Computers ein extrem hilfreiches Werkzeug für das menschliche Denken sein kann, um die Grenzen des menschlichen Wahrnehmens, Erinnerns und Denkens auszugleichen, auszuweiten.
Schon heute 2018 ist der Computer zu einem unverzichtbaren Bestandteil der Gesellschaft geworden. Das Wort von der ‚Digitalen Gesellschaft‘ ist keine Fiktion mehr.
ZEITGEIST
Der extrem kurze Rückblick in die Geschichte zeigt, wie schwer sich die Ausbildung und Verbreitung von Ideen immer getan hat. Und wenn wir uns die gesellschaftliche Realität heute anschauen, dann müssen wir konstatieren, dass selbst in den hochtechnisierten Ländern die gesamte Ausbildung stark schwächelt. Dazu kommt das eigentümliche Phänomen, dass das Alltagsdenken trotz Wissenschaft wieder vermehrt irrationale, gar abergläubische Züge annimmt, selbst bei sogenannten ‚Akademikern‘. Die Herrschaft von Dogmatismen ist wieder auf dem Vormarsch. Die jungen Generationen in vielen Ländern werden über mobile Endgeräte mit Bildern der Welt ‚programmiert‘, die wenig bis gar nicht zu wirklichen Erkenntnissen führen. Wissen als solches, ist ‚wehrlos‘; wenn es nicht Menschen gibt, die mit viel Motivation, Interesse und Ausdauer und entsprechenden Umgebungen zum Wissen befähigt werden, dann entstehen immer mehr ‚Wissens-Zombies‘, die nichts verstehen und von daher leicht ‚lenkbar‘ sind…
Einen Überblick über alle Blogeinträge von Autor cagent nach Titeln findet sich HIER.
Einen Überblick über alle Themenbereiche des Blogs findet sich HIER.
Das aktuelle Publikationsinteresse des Blogs findet sich HIER.