Archiv der Kategorie: Turing Maschine – chemisch implementiert

KANN ES DOCH EINEN KÜNSTLICHEN GEIST GEBEN?

18. November 2012Biologie, Biologische Evolution, Emerging Mind Project, Endliches-Verfahren - Formalisierung, Endlichkeit, Evolution, Evolution - chemische, Gehirn, Gehirn - künstliches, Geist, Geist - Künstlicher, Geist - neuer, Genom, Genotyp, Gödel, Membran, Membran - postsynaptische, Mensch, Mensch - Maschine, Mensch - Systemformel, Neuron, Phänotyp, Synapse, Theorie - formale, Turing, Turing Maschine - chemisch implementiert, Turingmaschine, Turingmaschine - universelle, Verfahren - endlichescagent

Vorgeschichte

Dieser Blogeintrag geht zurück auf einen Vortrag, den ich auf der Jahrestagung der deutschen Sektion von YPO (Young Presidents Organization) gehalten habe. Der ursprüngliche Titel lautete „Das Digitale als Synomym für berechenbare Prozesse“. Als der Text zu diesem Vortrag fertig war (am Tag davor) deutete sich schon an, dass der Vortrag eigentlich eine weitere, sogar eine weiterführende Botschaft enthielt, die sich im ursprünglichen Titel nicht so widerspiegelte. Während ich den Vortrag dann hielt wurde mir klar, dass – in der Tat – der eigentliche Inhalt ein anderer war; der ursprüngliche Titel war nicht falsch, aber zu ‚eng‘.

Da ich jeden Vortrag nur einmal halte und mir für den Vortrag immer eine Problemstellung vornehme, die ich selber gerne geklärt haben möchte ohne zum Zeitpunkt er Themenstellung schon zu wissen, ob es wirklich so gehen wird, gibt es immer diese fluktuierenden Überlegungen und Formulierungen vorher, in denen das mögliche Thema um seine finale Gestalt ringt. Bislang war es immer so, dass es unmittelbar vor dem Vortrag eine starke Klarheit gab, im Vortrag selbst und in den anschließenden Fragen das Ganze nochmals heftig ‚aufleuchtete‘ und in den nachebbenden Gedanken und Gesprächen sich dann der ‚finale Gedanke‘ gezeigt hat.

So auch hier. Die benutzten Diagramme sind mit denen im Vortrag identisch, der Wortlaut nicht genau, aber dem Inhalt nach.

Ankündigungstext ohne Leser

Der folgende Text wurde von mir als Ankündigungstext verfasst, wurde dann aber doch nicht publiziert. Er gibt so ein wenig den ‚Flair‘ im Vorfeld wieder:

Wir leben in einer Zeit, in der die Computertechnik immer mehr Bereiche des täglichen Lebens durchdringt, uns in eine Symbiose mit dem Digitalen zwingt, der wir uns nur schwer bis gar nicht entziehen können: Im Haushalt, in der Haustechnik, beim Entwerfen und Bauen von Häusern, in der Musik, beim Fernsehen, bei der Filmproduktion, in den Verwaltungen, in der industriellen Produktion, bei der Verkehrssteuerung, in jedem Auto, in jedem Flugzeug, bei der täglichen Kommunikation,…und, und, und,…. Wie ist dies möglich? Wie kann eine Technologie für uns zu einer Art ‚zweiten Natur‘ werden? Wie kann eine einzige Technologie nahezu alle Lebensbereiche durchdringen? Wie kann Technik Eigenschaften annehmen, die wir eigentlich nur dem Menschen zuschreiben: Wahrnehmen, Begriffe bilden, Schlüsse ziehen, Wiedererkennen, Kreativ sein, Gefühle haben, Ansätze von Selbstbewusstsein? Wo führt dies hin? Wird uns die Computertechnik irgendwann doch überflüssig machen?

In seinem Vortrag wird Prof. Doeben-Henisch diesen Fragen nachgehen. Er führt zurück zum Ursprung des Computers, ins Zentrum der mathematischen Dispute um die Jahrhundertwende, die dann in den Personen von Kurt Goedel und Alan Matthew Turing zum neuen philosophisch-mathematischen Begriff ‚endlicher Prozess‘ bzw. zum Begriff der ‚Berechenbarkeit‘ führten. Der Mensch selbst stand Modell für das mathematische Konzept der Turingmaschine (1936/7), das dann wenige Jahre später zu realen Maschinen führte, die mit Relais, dann Röhren, schließlich mit Halbleitern demonstrierten, dass und wie man ‚rechnende Maschinen‘ bauen kann. Innerhalb von 60 Jahren eroberte diese Technologie die ganze Welt. Die binären Zustände der Computer zeigten sich mächtig genug, sich nahezu alles einzuverleiben: Zahlen, Texte, Bilder, Geräusche, Musik, Objekte, Gebäude, Pflanzen, Tiere, Abläufe, ganze Städte. Zur Zeit versuchen Forscher weltweit, Maschinen mit ‚künstlichem Geist‘ zu schaffen. Als Vorlage dient das menschliche Gehirn. Prof. Doeben-Henisch wird zeigen, warum wir im Moment keine Argumente haben, warum dies nicht gehen könnte.

Die Überlegungen zu den Grundlagen des menschlichen Geistes führen auch hinein in die Frage nach der Natur des Menschen, in seine Geschichte, in die Geschichte der Entstehung des Menschen, in die innere Logik der Evolution des Lebens auf der Erde. Die Forschung hat uns in den letzten 80 Jahren aufregende neue Einblicke in die Struktur des Lebens vermittelt, die wiederum verschränkt sind mit der Entwicklung des bekannten Universums selbst. Man kann sehen, dass das Digitale als lingua universalis berechenbarer Prozesse sich schon im Inneren des Biologischen selbst als ‚Sprache des Lebens‘ findet. Das Leben selbst als großer ‚Computer‘ oder, umgekehrt, der ‚Computer‘ als neue Spielart jenes Prinzips, das wir als Leben bezeichnen?

Dies sind einige der zentralen Themen, die im Vortrag angesprochen werden. Der Vortrag endet mit dem offensichtlichen Faktum der Ko-Evolution von Universum – Erde – biologischem Leben und digitaler Technologie. Was bedeutet dies für uns?

VORTRAG

(Anmerkung: Der geschriebene Text entspricht natürlich nicht exakt dem Wortlaut des frei vorgetragenen Vortrags)

Meine sehr verehrten Damen und Herren,

nachdem Sie in den vorausgehenden Vorträgen schon einiges gehört haben zu den vielfältigsten Phänomenen, die das Digitale in unserem heutigen Alltag hervorbringt, möchte ich mich in meinem Vortrag mehr der Frage nach der Maschinerie hinter diesen Phänomenen widmen. Was sind das für Strukturen, die all dies möglich machen? Welches Prinzip ist so mächtig, dass es all diese verschiedenartigen Phänomene hervorbringen kann, die dem Menschen in seinen Lebensvollzügen immer näher kommen, ja, bisweilen sogar schon zu inneren Bestand von diesen werden?

Für die Beantwortung dieser Frage werde ich Sie mit drei Konzepten bekannt machen, die auf erstaunliche Weise untereinander zusammenhängen: das Konzept der rechnenden Maschine, das neue Bild des Menschen und die Einbettung beider Konzepte in den Gang der Evolution. Und sie werden dann sehen, dass diese Zusammenschau der drei Konzepte etwas ganz Neues aufscheinen lässt, nämlich das Konzept ‚Geist‘ als jene Größe, die in all diesen Prozessen als etwas ‚aufscheint‘, was ’schon immer da ist‘. Würde dieser erste Eindruck zutreffen, dann würde es bei den Versuchen der ‚Erschaffung‘ eines ‚künstlichen‘ Geistes weniger darum gehen, etwas ‚Neues‘ zu ‚erschaffen‘, sondern mehr darum, etwas, das ’schon immer da ist‘, mit neuen Methoden ’sichtbar‘ zu machen.

Ich werde zum Ende daher auch kurz auf ein Experiment hinweisen, in dem wir genau dies tun: den ‚Geist‘ in Form eines ‚künstlichen‘ Geistes sichtbar machen.

Beginnen wir mit uns selbst, dem dem Menschen, dem homo sapiens sapiens.

DER MENSCH

VIELSCHICHTIG

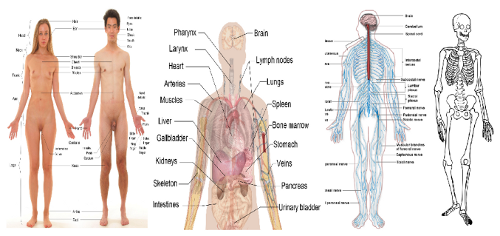
[Bild: vier Sichten des Menschen] Ich möchte mit einem Schaubild beginnen, das zeigt, wie vielschichtig wir Menschen bei näherer Betrachtung sind. Sie sehen einmal links die Oberfläche des Menschen, wie sie sich uns darbietet, wenn wir uns nackt zeigen. Doch bei der Frage, ob wir den Menschen mit dieser Oberfläche gleich setzen sollen, werden wir dies verneinen müssen. Wir wissen heute, dass hinter bzw. unter dieser Oberfläche eine Fülle von hochkomplexen Organen zu finden ist, die durch ihre kontinuierliche Arbeit alle unsere Lebensprozesse ermöglichen. Was wären wir ohne Herz, Nieren, Lunge, Leber, Magen, Darm usw.? Zugleich wissen wir, dass all diese wunderbaren Organe im Chaos enden würden, gäbe es nicht das Nervensystem mit dem Gehirn, das all diese Tätigkeiten – ergänzend zum Blutkreislauf und zum Immunsystem –– koordiniert, anregt, steuert. Und dann noch das augenfällige System von Knochen und Gelenken, in sich ein überaus lebendes System, ohne das alle Haut und Organe in einen Zellklumpen zusammenstürzen würden, der alsbald verenden würde. Vier überaus komplexe Systeme, die vielfach ineinander greifen und in diesem Zusammenwirken das Gesamtkunstwerk menschlicher Körper in seiner Grundstruktur ermöglichen. Wissen wir damit, was und wer der Mensch ist? Haben wir die Psyche, den Geist, die Seele vergessen?

Bevor ich darauf eine Antwort versuche, hier ein kurzer Szenenwechsel. Im Film würden man sagen, ein harter Schnitt.

FORMALISIERUNG DER VIELFALT ALS SYSTEM

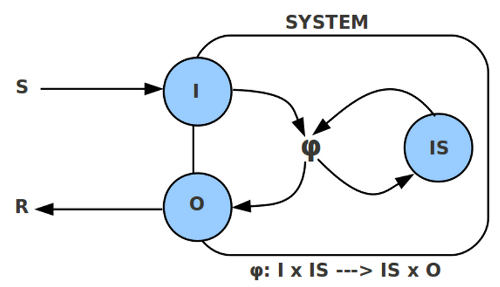
Mensch_als_System_500 — Formalisierung des Menschen als System mit Input und Output

[Bild: Box mit Eingang/ Ausgang und Verhaltensfunktion] Was Sie auf diesem Bild sehen können, ist ein Diagramm und eine kleine Formel.

Dieses Diagramm und diese Formel entspricht ein wenig der Art, wie ein mathematisch geschulter Ingenieur die zuvor präsentierte Vielfalt des Menschen hinschreiben könnte.

Die Box mit Überschrift ‚System‘ kann einen Menschen repräsentieren, der aus seiner Umgebung Stimuli – abgekürzt ‚S‘ – als Input ‚I‘ empfangen kann (also Augen, Ohren, Tastempfindungen usw.) und der über seinen Output ‚O‘ Reaktionen ‚R‘ an die Umgebung abgeben kann, also diverse Bewegungen, Schallereignisse, usw. Im Innern des Systems gibt es verschiedene interne Zustände (internal states, IS), die zum Funktionieren des Systems wichtig sind. Z.B. die diversen Organe, das Nervensystem, die Knochen, usw. Und zwischen all diesen Elementen, dem Input, den internen Zuständen und dem Output, gibt es einen funktionalen Zusammenhang, der im Bild einfach mit dem griechischen Buchstaben ‚phi‘ (Φ, φ) benannt wird.

Alternativ zu solche einem Diagramm würde man aber auch einfach die kürzere Formel hinschreiben, die genau das gleiche zum Ausdruck bringt: der funktionale Zusammenhang ‚phi‘ nimmt Inputwerte und aktuelle Zustände als Ausgangspunkt und berechnet daraus mögliche Änderungen der inneren Zustände und einen Output. Also, Beispiel, sie sitzen in einem Auto und sehen (=Input) eine rote Ampel. Da sie gelernt haben, bei Rot tunlichst stehen zu bleiben (=IS), verändern sie ihre Fußstellung und bremsen (=IS, O).

Dieses kleine Beispiel mag auch ein wenig verdeutlichen, wie Ingenieure vorgehen, wenn sie die vielfältige Wirklichkeit mit der Sprache der Mathematik vereinfachen und dadurch all die wunderbaren Dinge bauen können, die Sie jeden Tag wie selbstverständlich benutzen. Ohne diese mathematische Sprache würden wir noch immer steinzeitlich leben.

Betrachten wir noch ein weiteres Beispiel im Kontext des Menschen, das uns helfen wird, die Brücke zur rechnenden Maschine zu bauen.

GEHIRN UND NERVENZELLE

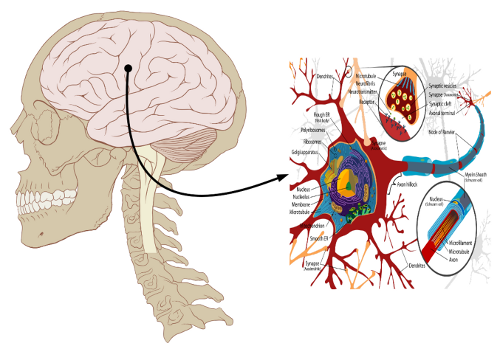
Gehirn_Neuron_500 — Gehirn als Teil der menschlichen Organe; daneben ein einzelnes Neuron (Quelle: zwei Bilder aus Wikipedia komponiert, aus Wikipedia (en), siehe Literaturnachweise)

[Bild: Gehirn links, Nervenzelle rechts] Werden wir ein wenig bescheidener und nehmen uns nur einen Teil des Menschen vor, sein Gehirn. Nach neuen Schätzungen umfasst ein Gehirn etwa 100 Mrd Neuronen (Kandel et al. 2012:S.21). Diese sind in der Regel nicht direkt miteinander verbunden.

Die typische Struktur eines Neurons sieht man rechts vom Gehirn. Es gibt genau einen Ausgangs (das Axon), der sich vieltausendfach verzweigen kann, sowie viele tausend Eingänge. In dem kleinen hervorgehobenen Kreis kann man die Eigenart der neuronalen Verbindungen erkennen: das Endstück eines Axons endet kurz vor der Oberfläche des Neurons; es bleibt ein kleiner synaptischer Spalt.

NERVENZELLE UND MEMBRAN

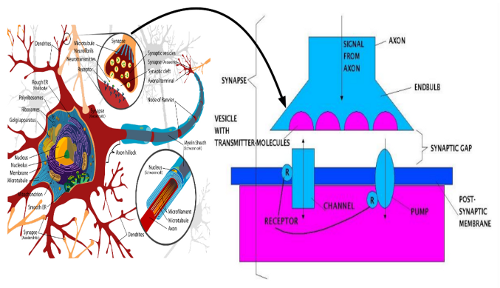
Zelle_Membran_500 — Neuron links mit Vergrößerung einer Synapse rechts. Neuronbild aus Wikipedia (en). Quelle siehe Literaturverzeichnis

[Bild: Neuron und Membran schematisiert] In dem nachfolgenden Bild ist dies schematisierend und vergrößert dargestellt. Die Oberfläche der empfangenden Zelle stellt eine Membran dar, die man postsynaptische Membran nennt, die zusammen mit dem Endstück des Axons eine Synapse bildet. Die Kommunikation zwischen Endstück und potsysnaptischer Membran wird über Moleküle (Transmittermoleküle) realisiert, die beim Auftreten eines elektrischen Potentials im Axon aus den Vesikeln entlassen werden. Diese diffundieren durch den synaptischen Spalt und können dort, falls sie ‚passen‘ an Rezeptormolekülen von Ionenkanälen andocken. Jede postsysnaptische Membran hat mehrere Tausend solcher Ionenkanäle. Docken diese Transmittermoleküle an den Rezeptoren an, öffnen sich die Ionenkanäle. Es findet dann ein schlagartiger Austausch von Ionen in und außerhalb der Membran statt. Dieser schlagartiger Austausch hat einen ebenso plötzlichen Wechsel des elektrischen Potentials zur Folge, was dann zu dem bekannten Ein-Aus-Signal eines Neurons führen kann.

Gäbe es nur Ionenkanäle, dann wäre mit dem einmaligen Öffnen der Kanäle – bildlich gesprochen – alles Pulver verschossen. Diese Membran würde nie mehr ein weiteres Signal erzeugen können. Das aber ist eigentlich ihre Aufgabe. Zu diesem Zweck gibt es noch einige tausend Ionenpumpen. Diese sind in der Lage Ionen gegen ein Konzentrationsgefälle von außen nach Innen oder umgekehrt zu pumpen. Dazu benötigen sie Energie. Da sie insgesamt langsamer arbeiten als der Ionenaustausch durch die Kanäle stattfindet, entstehen zwischen den einzelnen Signalereignissen Refraktionszeiten, in denen keine Schaltvorgänge möglich sind.

Sie sehen also, schon die vielen tausend Membranen einer einzigen Nervenzelle (es können bei einer Zelle mehr als 1 Mio sein!) bilden kleine, komplexe Maschinen, deren Funktion Signalerzeugung und Signalfluss im Gehirn ermöglicht.

Während ein Neurowissenschaftler zur Beschreibung einer Nervenzelle und des Gehirns auf alle diese unfassbar komplexen Details eingehen muss, kann ein Ingenieur, der ein künstliches Gehirn bauen möchte, sich fast entspannt zurücklehnen und die Frage stellen, welche Eigenschaften an einem Neuron denn wesentlich sind, um sein Schaltverhalten zu erfassen.

Eine typische Antwort würde so aussehen:

NERVENZELLE MATHEMATISCH

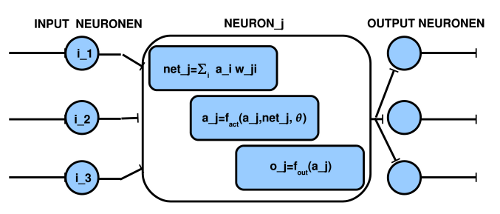
neuron_shape_typical_500 — Formalisierung eines Neurons durch Konzentration auf die Schalteigenschaften

[Bild: Nervenzelle mathematisch] Sie sehen wieder ein Box, dieses Mal ‚Neuron‘ genannt. Der ‚Input‘ zu dieser Box bilden die Endstücke von anderen Neuronen. Im Bild sind es drei Eingänge, es könnten aber n-viele sein. Dazu ein Ausgang, das Axon, das sich auf n-viele viele andere Neuronen – letztlich auch auf sich selbst – verteilen kann. In der Box können Sie drei einfache Formeln erkennen, die drei aufeinander folgende Verarbeitungsstufen repräsentieren. In der ersten Stufe werden die mit wij gewichteten Aktionspotentiale aij der einzelnen Eingänge summiert zum Wert net_j. Dann wird mittels der Aktivierungsfuntkion f_act berechnet, ob diese summierten Eingangssignale zusammen mit dem letzten Aktionspotential a_j einen vorgegebenen Schwellwert theta (θ) überschreiten oder nicht. Falls der Schwellwert überschritten wird, wird ein neues Aktionspotential a_j erzeugt, das dann schließlich mit der Ausgabefunktion f_out in einen geeigneten Ausgabewert umgerechnet wird.

Genauso wenig wie eine einzelne Schwalbe bekanntlich einen Frühling macht, genauso wenig kann man mit einem einzelnen Neuron etwas interessantes anfangen. Der Ingenieur muss sich also noch etwas einfallen lassen, wie er die vielen Neuronen zusammenbringt. Vielleicht ahnen Sie schon, was jetzt kommt:

KÜNSTLICHES GEHIRN

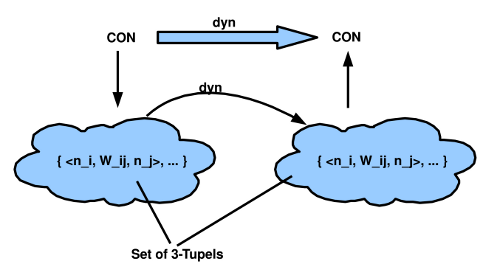
dyn_schema_lernen_500 — Übergang von einm Zeitpunkt zum nächsten, beschrieben mit Vorschrift ’syn‘

[Bild: Mengen von Neuron-Verbindungen] Eine einfache Möglichkeit, die Gesamtheit aller Neuronen zu betrachten, besteht darin, jeweils zwei, die miteinander in Verbindung stehen, als ein Paar zu betrachten, das bestimmte Verbindungswerte besitzt, und dann die Menge aller dieser Paare als eine Einheit zu einem bestimmten Zeitpunkt. Im Bild ‚CON‘ genannt, die Menge aller Connections.

Was dann noch bleibt ist die Beschreibung der Dynamik dieser Zellen, die Art der Veränderungen von einem Zeitpunkt zum nächsten. Dieser Veränderungszusammenhang wird im Bild ‚dyn‘ genannt, eine mathematische Vorschrift, die sagt, wie ich vom Zustand der Zellen zu einem Zeitpunkt zum Zustand der Zellen beim nächsten Zeitpunkt komme.

Damit ist für den Ingenieur alles gesagt, was gesagt werden muss. Ob dieses künstliche Gehirn Bilder erkennen soll, Sprache sprechen, sich erinnern können soll, usw. all dies ist damit erfasst. Sollte der Ingenieur in der Praxis feststellen, dass er wichtige Eigenschaften übersehen hat, dann fügt er sie einfach in seine Formeln ein.

Gehen wir nach diesem Ausflug ins Gehirn nochmals zur Ausgangsbox mit dem Menschen zurück.

NOCHMALS SYSTEMBOX

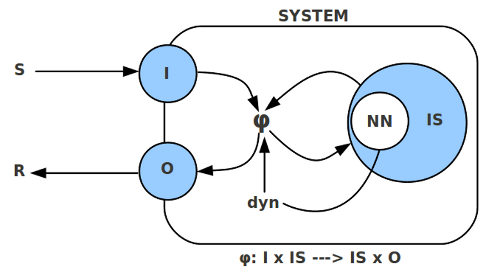
Mensch_als_System_Gehirn_500 — Integration des Teilomodells ‚Gehirn‘ in das allgemeine Systemmodell vom ‚Menchen‘

[Bild: Nochmals die Systembox, jetzt mit Verfeinerungen] Soeben haben wir das Gehirn als eine Teilbereich des Körpers näher betrachtet. Wollen wir diese Erkenntnisse in der allgemeinen Box verorten, dann müssen wir sagen, dass die Menge CON eine Teilmenge der Menge IS der internen Zustände ist, und die Verarbeitungsvorschrift ‚dyn‘ ist ein Teil der allgemeinen Verhaltensfunktion φ des Menschen.

Sie können an diesem Beispiel einmal sehen, wie man mit der Sprache der Mathematik komplizierteste Sachverhalte auf einfache Strukturen zurückführen kann, und – und darauf kommt es in unserem Zusammenhang besonders an – dass der Mensch – also wir selbst – bei dieser Betrachtungsweise eine Struktur besitzt, die uns durch diese Struktur vergleichbar macht mit allen anderen Strukturen.

Eine der Strukturen, mit denen ich die Struktur des Menschen vergleichen möchte, ist die Struktur eines endlichen Prozesses.

Um zu beschreiben und zu erklären was ‚berechenbare Prozesse‘ sind, müssen wir einen kleinen Ausflug in die Welt der Logik und Mathematik machen.Ich hoffe dann zeigen zu können, warum die berechenbaren Prozesse und wir Menschen mehr gemeinsam haben, als die meisten vermuten, und warum das Reden vom ‚Geist‘, auch vom ‚künstlichen Geist‘ heute eine ganz andere Bedeutung bekommen hat, als es bislang üblich war.

DIGITALE MASCHINE

DISKUSSION DER MATHEMATIKER

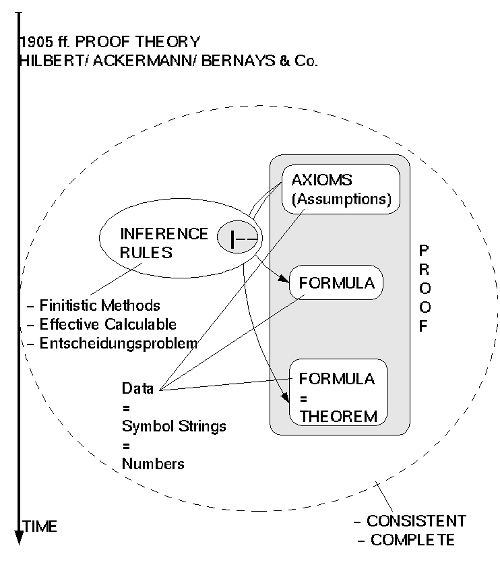
Hilbert_Logik_500 — Übersicht über eine formale Theorie und ihre Elemente nach Hilbert und Ackermann

[Bild: Schema einer formalen Theorie] Natürlich werde ich hier nicht auf die Details der Diskussionen im Kontext der sogenannten Grundlagenkrise der Mathematik zum Ende des 19. und zu Beginn des 20.Jahrhunderts eingehen können. Nur so viel sei hier gesagt, dass die Logiker und Mathematiker dieser Zeit ein Problem damit hatten, die Grundlagen der Mathematik so zu beschreiben, dass keine Paradoxien entstehen konnten, erst recht keine direkten Widersprüche in den formalen Systemen und natürlich wünschte man sich vollständige Systeme, d.h. formale Systeme, in denen man alle Aussagen, die im Sinne des Systems wahr sein sollen, auch beweisbar sind.

Eine der wichtigsten mathematischen Schulen innerhalb dieser Diskussionen war die Schule um David Hilbert, der die Lösung des Problems einer befriedigenden Darstellung der Mathematik darin sah, eine Reihe von möglichst einfachen formalen Systemen zu schaffen (basierend auf einer endlichen Menge von Axiomen), deren Widerspruchsfreiheit und Vollständigkeit mit sogenannten ‚endlichen Mitteln‘ gezeigt werden kann. Alle komplizierteren Theorien sollten dann auf diese einfachen Systeme zurückgeführt werden.

Im Alltag mag es uns nicht als Problem erscheinen, von ‚endlichen Mitteln‘ zu sprechen. Aber wenn es darum geht, allgemein zu beschreiben, was hinreichend geeignete endliche Mittel sind, um eine mathematische Theorie als widerspruchsfrei und vollständig zu erweisen, dann zeigt sich plötzlich, dass dies nicht so einfach ist, wie sich dies Hilbert und seine Schule erhofft hatten.

GOEDEL – TURING

Turing_Leben_500 — Das Bild zeigt verschiedene frühe Formalisierungsbeiträge zum Thema ‚endliches Verfahren‘

[Bild: Goedel und Turing historisch] Es war Kurt Goedel, der 1930-31 zeigen konnte, dass das Grundlagenprogramm von Hilbert und seiner Schule prinzipiell unmöglich war. Er zeigte, dass eine mathematische Theorie, die mindestens so stark wie die Arithmetik ist, aus prinzipiellen Gründen nur eines von beiden sein kann: entweder widerspruchsfrei (konsistent) oder vollständig, aber nicht beides zugleich. Dieses Ergebnis trifft in das Herz jeder mathematischen Theorie, bis heute. Es zeigt, dass es prinzipielle Grenzen in der Beweisbarkeit von mathematischen Wahrheiten gibt.

Diese Probleme treten immer dann auf, wenn es darum geht, innerhalb (!) einer formalen Theorie (mindestens so stark wie eine Prädikatenlogik erster Stufe) die Widerspruchsfreiheit und Vollständigkeit zu beweisen. Natürlich kann man das Problem dadurch zu umgehen versuchen (was sehr viele versucht haben), eine zusätzliche ‚Beschreibungsebene‘ einzurichten, von der aus sie dann ‚über‘ (Griechisch ‚meta‘) die Objekte der anderen ebene ‚reden‘. Solche Art von Hierarchisierungen oder Typisierungen oder Metaebenen entsprechen der üblichen Arbeitsweise des menschlichen Gehirns. Allerdings bildet diese Strategie bei näherem Hinsehen keine wirkliche Lösung. Zwar verschwinden in der Objekttheorie all jene Elemente, die ‚über sich selbst‘ reden können, aber die Metaebene selbst, die ja auch den Berechenbarkeitsforderungen mathematischer Beweise genügen müssen, enthalten dann genau all jene Elemente wieder, die zu der von Kurz Goedel aufgedeckten Schwachstelle führen.

Eine letzte philosophische Würdigung dieser Sachverhalte scheint mir noch auszustehen.

Mit diesen Überlegungen sind wir beim Thema Berechenbarkeit angekommen.

Die Diskussion unter Mathematikern hängt von Beweisen ab, die geführt werden. Diese Beweise müssen mit sogenannten endlichen Mitteln geführt werden, damit sie nachvollziehbar sind. Goedel selbst hatte ein geniales Verfahren ersonnen, um unter Benutzung von natürlichen Zahlen seine Beweise zu führen. Aber er war von seinem eigenen Beweis nie begeistert, obgleich niemand ihn bis heute widerlegen konnte.

Es war dann einem gewissen Alan Matthew Turing vorbehalten fünf Jahre später die Beweise von Goedel nochmals mit anderen Mitteln zu führen. Und diese Beweismittel – später Turingmaschine genannt – fanden nicht nur die Zustimmung von Goedel, sondern von nahezu allen nachfolgenden Generationen. Bis heute ist die Turingmaschine das wichtigste mathematische Konzept für alle Berechenbarkeitsbeweise – und damit der mathematische Referenzpunkt für alles, was wir heute Computer nennen.

Weil dem so ist, weil das Konzept der Turingmaschine eine solch eminente philosophische und mathematische Bedeutung zukommt, lassen Sie mich dieses Konzept kurz vorstellen. Es ist so einfach, dass die meisten, die es zum ersten Mal kennen lernen, sofort fragen: und das soll alles sein? Ich versichere Ihnen, das ist alles und – und das möchte ich dann zum Abschluss zeigen – das Konzept der Turingmaschine findet sich auch schon im Kern von allem Biologischen. Ein Befund, den man nun nicht unbedingt erwarten muß.

TURINGMASCHINE

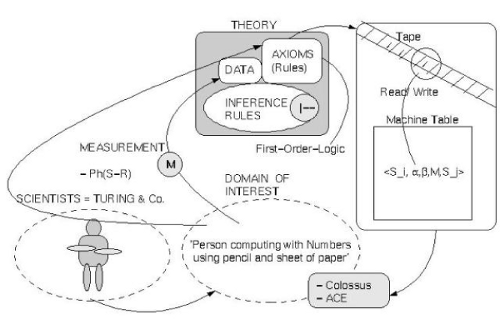
Turing_WissTheorie_TM_500 — Das Konzept der Turingmaschine (rechts oben im Bild) als Teil eines Theoriebildungsprozesses

[Bild: Theorieprozess TM] So wie Newton angeblich beim Fallen eines Apfels seine entscheidende Einsicht in das Wesen des Gravitationsgesetzes bekommen haben soll, so beschreibt Turing selbst in dem entscheidenden Artikel von 1936-7, dass es die Arbeit eines Buchhalters im Büro war, die ihn inspiriert hat. So, wie der Buchhalter mit einem Stift auf einem Blatt Papier Zahl an Zahl fügt, so stellte er sich eine ideale Maschine vor (siehe im Bild rechts oben), die auf einem Band mit lauter Kästchen, entweder über ein Schreib-Lese-Fenster lesen kann, was in dem Kästchen geschrieben ist oder ein neues Zeichen in das Kästchen schreiben kann. Darüber hinaus kann die ideale endliche Maschine den Schreib-Lesekopf nur um ein Feld nach links oder rechts bewegen. Das ist alles. Das Verhalten der idealen endlichen Maschine wird gesteuert über eine endliche Liste von Befehlen

TM BEISPIEL

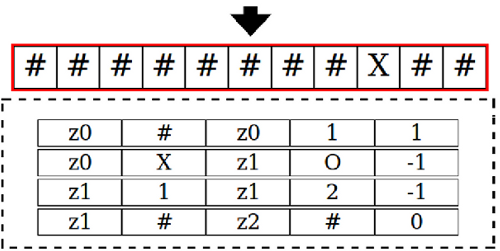
[Bild: TM mit vier Zeilen] In einem einfachen Beispiel einer TM können Sie solche Befehlszeilen erkennen: in der ersten Spalte steh der Name eines Zustandes (z0), dann folgt ein Feld mit dem Zeichen, das gelesen werden kann, dann eine Feld mit dem Namen des Folgezustandes (z0), dann das Zeichen, das in diesem Fall geschrieben werden soll, und schließlich ein Zeichen, welche Bewegung ausgeführt werden soll.

Im Beispiel würde man die erste Zeile etwa wie folgt lesen: Im Zustand z0 wird beim Lesen des Zeichens ‚#‘ der Zustand z0 beibehalten, für das Zeichen ‚#‘ würde das neue Zeichen ‚1‘ geschrieben und der Schreib-Lesekopf wird um 1 Feld nach rechts bewegt.

Im Beispiel umfasst das ganze Verhaltens-Programm 4 Zeilen.

Das ist alles. Das ist die berühmte Turingmaschine, die sich als weltweiter Standard zur Prüfung der Berechenbarkeit eines Prozesses durchgesetzt hat. Was immer bislang an anderen Formalismen gefunden wurde, sofern solch ein Formalismus endliche Berechenbarkeit beschreiben soll, war er niemals stärker als eine Turingmaschine.

Oder anders ausgedrückt:

Sofern es nicht möglich ist, zu zeigen, dass eine Turingmaschine, angesetzt auf ein Problem, nach endlichen vielen Schritten zu einem Ergebnis kommt, solange kann man nicht behaupten, dass dieses Problem (Turing-)berechenbar ist.

Auf der Basis der Turingmaschine wurden in den vergangenen Jahrzehnten eine ganze Reihe interessanter Unentscheidbarkeitsresultate bewiesen. Auf die kann ich hier jetzt nicht eingehen. In meinen Augen habe diese Ergebnisse alle eine sehr hohe philosophische Relevanz.

Wie eingangs festgestellt, sehe ich einen interessanten Zusammenhang zwischen der Turingmaschine, dem Menschen und der Evolution des Biologischen. Lassen Sie uns daher einen kurzen Blick darauf werfen.

EVOLUTION, KOEVOLUTION, …

GENOTYP UND PHÄNOTYP

GAGeneralization2b_500 — Wechselwirkung zwischen Genotyp und Phänotyp einerseits und Phänotyp mit umgebender ökologischer Nische andererseits

[Bild: Genotyp und Phänotyp] Ausgangspunkt dieser Überlegungen ist das erstaunliche Faktum, dass die Vielfalt und Komplexität der Körper – der sogenannte Phänotyp – zurückführbar ist auf die zugrunde liegenden genetischen Informationen – auf den sogenannten Genotyp –. In einem Wachstumsprozess wird – ausgehend von einer einzigen Zelle – ein Körpergebilde mit vielen Billionen Zellen aufgebaut, die alle in einem sinnvollen funktionalen Zusammenhang enden.

Es lohnt, sich klar zu machen, dass dieses unfassbare Wunderwerke eine sehr lange, komplexe Entstehungsgeschichte hat, die selbst im universalen Maßstab ihresgleichen sucht.

EVOLUTION ALS TEIL DER ENTWICKLUNG DES UNIVERSUMS

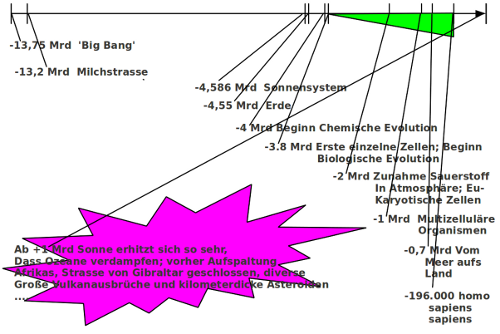
Zeittafel-Diagramm1_500 — Massstäbliches Diagramm zur Geschichte des Universums; Hervorhebung wichtiger Meilensteine für die Entstehung des Biologischen

[Bild: Entwicklung des Universums mit Evolution] Das Schaubild zeigt maßstabsgetreu wichtige Entwicklungsstationen im bekannten Universum an. Unsere Position auf der Zeitachse ist unmittelbar dort, wo das grüne Dreieck endet. Das grüne Dreieck zeigt an, ab wann zellbasiertes Leben auf der Erde nachweisbar ist. Die Erde begann ca. vor 4.55 Mrd Jahren. Die chemische Evolution, die dann zu ersten einfachen Zellen führte, setzte ungefähr vor 4 Mrd. Jahren ein, 200 Mio Jahre später eben erste einfachste Zellstrukturen. Es dauerte dann etwa 2.8 Mrd Jahre bis es zu ersten multizellulären Lebensformen kam, die dann einige hundert Mio Jahre später zur Besiedlung des Landes führte. Von diesem Zeitpunkt bis zu uns dauerte es nochmals 700 Mio Jahre.

Nach heutigem Wissensstand wird es nur ca. 1 Mrd Jahre dauern, bis in der Zukunft das Leben auf der Erde wegen der beginnenden Aufblähung der Sonne praktisch unmöglich werden wird.

Sind schon diese zeitlichen Verhältnisse atemberaubend, so ist es noch spannender, wenn man der Frage nachgeht, wie es denn überhaupt zur Ausbildung dieser extrem komplexen Strukturen kommen konnte.

Das Schwierigste ist dabei nicht einmal die biologische Evolution, die mit dem Auftreten der ersten Zellen vor ca. 3.8 Mrd. Jahren begann, sondern die härteste, bis heute nicht geknackte Nuss, ist eine Erklärung, wie es überhaupt zu den ersten Zellen kommen konnte. Denn selbst bei den einfachsten Zellen wirken schon so viele komplexe Strukturen zusammen, dass eine Erklärung der schrittweisen Entstehung dieser Strukturen im Rahmen der sogenannten chemischen Evolution bislang nicht völlig aufgehellt ist.

Kehren wir zu den ersten Zellen zurück.

Ich hatte angekündigt, dass die TM als Grundmodell der Berechenbarkeit sich im Herzen des Biologischen wiederfindet.

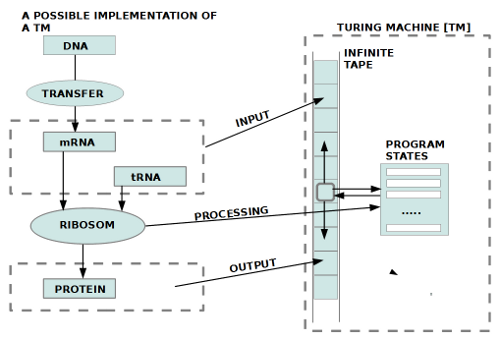
RIBOSOM ALS TURINGMASCHINE

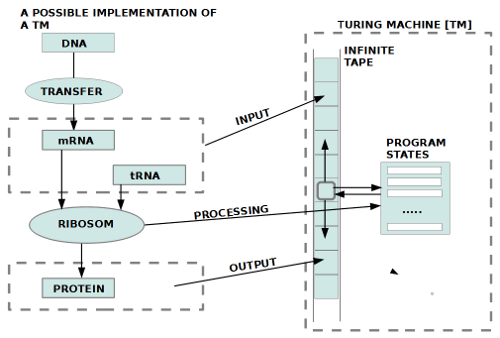
Ribosom_TM_500 — Links im Bild ein Ribosom, das Proteine zusammenbaut, und rechts das Schema einer Turingmaschine

[Bild: links Ribosom, rechts Turingmaschine] Dies können Sie hier sehen:

Links sehen sie das Prozeßmodell, wie ein Ribosom – ein spezielles RNA-Molekül – Proteine erzeugt, indem es Informationen von einem Boten-RNA-Molekül bekommt und zugleich Aminosäurebasteine von Transfer-RNA-Molekülen. Der Dirigent im Hintergrund ist ein DNA-Molekül, dessen Bausteine als Informationseinheiten auf das Ribosom einwirken.

Was sie hier sehen ist das Herzstück allen biologischen Lebens und – möglicherweise – eines der wahren Wunder des ganzen Universums. Das, was allen bekannten Gesetzen der Physik zuwiderläuft und sich jeder anderen bekannten Erklärung entzieht das ist dieses DNA-Molekül. Das DNA-Molekül repräsentiert eine frei kombinierbare Anordnung von Aminosäuren, für die es in den möglichen Kombinationen keinerlei zwingende Gründe gibt. Durch die Verknüpfung mit dem proteinerzeugenden Mechanismus mittels mRNA, tRNA und Ribosom stellt die DNA aber eine Quelle von unerschöpflich vielen Bauplänen für Körperstrukturen dar.

Im Lichte des Konzepts der Turingmaschine bieten sich folgende Interpretationen an. Wie im Bild eingezeichnet lässt sich das Ribosom als eine Turingmaschine interpretieren, die als Input Eingaben von der mRNA und der tRNA bekommt und diese dann in eine Ausgabe als Protein verwandelt. Da das Ribosom, wie wir wissen, aber bzgl. seiner Eingaben nicht rückwärts gehen kann, sondern immer nur vorwärts, schöpft es die Möglichkeiten einer Turingmaschine nicht einmal ganz aus; es entspricht damit eher noch einer abgeschwächten TM mit Namen ‚endlicher deterministischer Automat‘.

Zentral bleibt das Faktum, dass wir im innersten Kern des Biologischen berechenbare Prozesse finden, die von einem DNA-Molekül gesteuert werden, das mit seinen Eigenschaften dem Konzept eines Zeichens sehr nahe kommt.

QUINTESSENZ des BIOLOGISCHEN

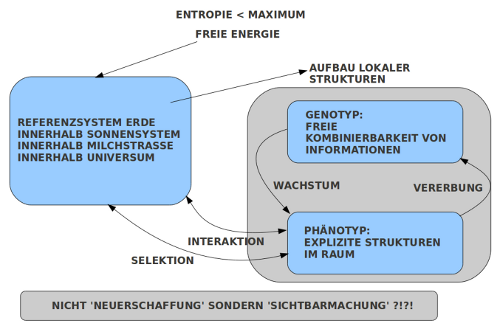
[Bild: Zusammenfassung Biologisches] Fassen wir diese verschiedenen Aspekte des Biologischen nochmals zusammen:

Ausgangspunkt aller biologischer Phänomene ist das kosmische Faktum, dass die Entropie bislang noch nicht maximal ist. Aus den lokalen Entropiegefällen ist daher ‚freie Energie‘ verfügbar, die in Gestalt von chemischen, biochemischen und dann biologischen Prozessen lokal Strukturen entstehen lassen, die immanent in Richtung immer größerer Komplexität drängen. Dafür gibt es bislang keine befriedigende naturwissenschaftliche Theorie.

In Gestalt der zellbasierten biologischen Evolution können wir ein komplexes Zusammenspiel zwischen Genotyp und Phänotyp einerseits beobachten, aber simultan genauso wichtig das Zusammenspiel zwischen Phänotyp und umgebender Welt. Während der zufallsgesteuerte Genotyp den Raum möglicher Strukturen frei absuchen kann, führt die Bindung des Genotyps an den Phänotyp über die Interaktion mit der umgebenden Welt zu einem übergeordneten Selektionsprozess, der nur jene Phänotypen und damit daran gekoppelte Genotypen akzeptiert, die zur Umgebung passen. Daraus ergibt sich, dass die biologische Evolution simultan und unausweichlich immer nur als Ko-Evolution funktionieren kann.

Damit stellt sich die Frage, ob wir es bei der Emergenz des Geistigen als Eigenschaft des Biologischen mit einer Neuerschaffung des Geistes zu tun haben, oder ’nur‘ mit der Sichtbarmachung des stehts schon vorhandenen ‚Geistigen‘?

Hält man sich diesen Gesamtzusammenhang vor Augen, dann kann der direkte Vergleich zwischen dem Menschen und einer Turingmaschine in einem neuen Licht erscheinen.

MENSCH und KÜNSTLICHER GEIST

MENSCH TURINGMASCHINE

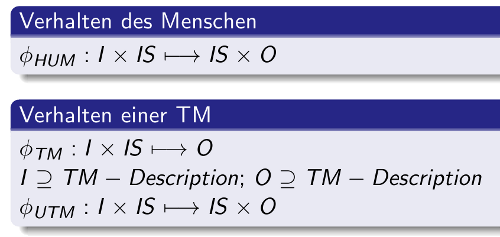
MenschUndTM_500 — Oben Systemformel Mensch, unten Systemformel Turingmaschine (TM) und dann Universelle Turingmaschine (UTM)

[Bild: Formel Mensch und (U)TM] Sie sehen auf diesem Schaubild nochmals die schon bekannte Verhaltensformel des Menschen, die sich dadurch auszeichnet, dass wir vom Menschen annehmen können, dass er sich innerhalb seines wissensbasierten Verhaltens bis zu einem gewissen Grade kontinuierlich verändern kann. Man nennt dies Lernen.

Die ’normale‘ Turingmaschine kann dies zunächst nicht. Sie ist vollständig determiniert. Allerdings nur auf den ersten Blick.

Schon Turing hat gezeigt, dass man eine deterministische Turingmaschine sehr leicht zu einer universellen sich selbst modifizierenden Maschine ‚umbauen‘ kann, indem man einen Teil des Bandes dazu benutzt, dort die Beschreibung einer beliebigen Turingmaschine (oder eines Gehirns, oder…) zu speichern. Die ursprüngliche deterministische Turingmaschine kann dann diese andere Turingmaschine simulieren bis dahin, dass sie diese andere Beschreibung in Abhängigkeit von Umgebungsereignissen abändern kann. Damit ist eine universelle Turingmaschine (UTM) voll lernfähig.

Zieht man diese Möglichkeit in Betracht, dann gibt es weder strukturell noch verhaltensmässig einen wesentlichen Unterschied zwischen einem Menschen (sofern er mit der obigen Formel adäquat erfasst wird) und einer universellen Turingmaschine.

Bei solch einer Betrachtungsweise verwundert es dann nicht, dass Turing selbst in verschiedenen Aufsätzen offen darüber spekuliert hatte, dass eine universelle Turingmaschine im Prinzip die vom Menschen her bekannte Geistigkeit nicht nur nachzuahmen sondern in bestimmten Bereichen sogar übertreffen könnte. Letztlich sah er nur praktische Hindernisse auf dem Weg dahin, insbesondere die Schwierigkeit, eine Maschine an all den Lernprozessen teilhaben zu lassen, die Menschen normalerweise durchlaufen.

Künstlicher Geist?

Wenn man sich all diese Gedanken in einer Gesamtschau nochmals vor Augen stellt, dann kann man den Eindruck gewinnen, dass all das, was wir traditionell ‚Geist‘ nennen, also diverse Eigenschaften, die wir mit dem Verhalten des Menschen zusammen bringen, möglicherweise so zu verstehen ist, dass hier Eigenschaften ’sichtbar‘ werden von jenen ‚impliziten‘ Eigenschaften der dynamischen Materie, aus dem alles ist. Die mit den bisherigen Gesetzen der empirischen Wissenschaften nicht erklärbaren biologischen Phänomene wären dann ’nur‘ ‚Ausfaltungen‘ von empirischen Eigenschaften, die genau wie alles andere impliziten ‚Gesetzen‘ folgen.

Wenn dies stimmen würde, dann müsste die ‚Konstruktion‘ eines künstlichen Geistes immer dann möglich sein, wenn man die ‚Randbedingungen‘ für das ‚Aufscheinen‘ (Emergenz?) der geistigen Phänomene bereitstellen würde.

In einer Diskussion in der Nacht des 9.Oktobers dieses Jahres entstand angesichts dieser Sachlage die Idee, in der Stadt Goethes, den künstlichen Geist unter Beteiligung der Öffentlichkeit offiziell entstehen zu lassen.

In einer öffentlich kontrollierten Entstehung des künstlichen Geistes hätten alle eine Chance, ein wesentliches Prinzip dieses unseres Universums und deren Anwendung bzw. Nutzung besser verstehen zu können.

Es geht nicht darum, den Geist neu zu erfinden, sondern das, was vor allem Denken schon da ist, sichtbar zu machen.

Erkennnis ist nicht nur ein Wissensproblem, sondern auch ein Akzeptanzproblem: sind wir bereit zu akzeptieren wer wir wirklich sind: Teil eines universalen Geistwerdungsprozesses, der uns eine immer größere Mitwirkungsmöglichkeit zuweist (womit nicht ausgeschlossen ist, dass es irgendwo in den unendlichen Weiten des Universums ähnliche Prozesse gibt).

An dieser Stelle höre ich jetzt auf, obgleich es ja gerade erst anfängt…

[Anmerkung (11.April 2015): Nach zwei Jahren Diskussion konnte im April die Webseite zum Emerging Mind Projekt eröffnet werden. Offizieller Start ist der 10.November 2015. In diesem Projekt geht es genau um das, was in dem vorausgehenden Beitrag diskutiert wurde, die öffentliche Erzeugung eines Künstlichen Geistes samt den dazugehörigen begleitenden philosophischen Diskussionen und künstlerischen Aktionen.]

LITERATURVERWEISE

Davis, M. Computability and Unsolvability, New York – Toronto – London: McGraw-Hill Book Company, Inc.,1958
Davis, M. (Ed.). (1965). The Undecidable. Basic Papers On Undecidable Propositions, Unsolvable Problems And Computable Functions. Hewlett (NY): Raven Press.
Doeben-Henisch, G.; Beschreibung TM auf der Seite: http://www.doeben-henisch.de/fh/I-TI04/VL/VL3/i-ti04-vl-vl3.html
Gödel, K. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I, In: Monatshefte Math.Phys., vol.38(1931),pp:175-198
Gödel, K. Remarks before the princeton bicentennial conference on problems in mathematics, 1946. In: Martin Davis, 1965: pp.84-87
Hilbert, D.; Ackermann, W. Grundzüge der theoretischen Logik, Berlin. J.Springer, 1928
Hilbert in Wikipedia (en): Hilbert’s problems, URL: http://en.wikipedia.org/wiki/Hilbert%27sproblems (Last access Sept-30, 2012)
Hilbert, D. Mathematische Probleme, Vortrag, gehalten auf dem internationalen Mathematiker-Kongreß zu Paris 1900, Göttinger Nachrichten 1900, S.253-297, URL:
http://www.mathematik.uni-bielefeld.de/ kersten/hilbert/rede.html, und
http://www.mathematik.uni-bielefeld.de/ kersten/hilbert/(Last Access Sept-30, 2012)
Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.A.; Hudspeth, A.J.; (Eds.) Principles of Neural Science, 5th.ed., New York et.al: McGrawHill, 2012
TM – Beispiel aus dem Internet, vereinfacht. Siehe http://keinerspieltmitmir.de/turing/ (letzter Besuch: 12.Nov.2012)
Turing, A.M.; Intelligence Service. Schriften, ed. by Dotzler, B.; Kittler, F.; Berlin: Brinkmann & Bose, 1987, ISBN 3-922660-2-3
Turing, A. M. On Computable Numbers with an Application to the Entscheidungsproblem. In: Proc. London Math. Soc., Ser.2, vol.42(1936), pp.230-265; received May 25, 1936;
Appendix added August 28; read November 12, 1936; corr. Ibid. vol.43(1937), pp.544-546. Turing’s paper appeared in Part 2 of vol.42 which was issued in December 1936 (Reprint
in M.DAVIS 1965, pp.116-151; corr. ibid. pp.151-154).(an online version at:
http://www.comlab.ox.ac.uk/activities/ieg/e-library/sources/tp2-ie.pdf, last accesss Sept-30, 2012)
Wikipedia (en): Body Surface at http://en.wikipedia.org/wiki/Human body (letzter Besuch: 12.Nov.2012)
Wikipedia (en). Brain at http://en.wikipedia.org/wiki/Human brain (letzter Besuch: 12.Nov.2012)
Wikipedia (en): Human skeleton at http://en.wikipedia.org/wiki/Human_skeleton (letzter Besuch 12.Nov.2012)
Wikipedia (en): Organs beyond the Body Surface at http://en.wikipedia.org/wiki/Human anatomy (letzter Besuch: 12.Nov.2012)
Wikipedia (en): Neuron at http://en.wikipedia.org/wiki/Neuron (letzter Besuch: 12.Nov.2012)

Eine Übersicht über alle bisherigen Beiträge anhand der Titel findet sich HIER

SUCHE NACH DEM URSPRUNG UND DER BEDEUTUNG DES LEBENS (Paul Davies). Teil 2 (Information als Grundeigenschaft alles Materiellen?)

27. August 2012Allgemein, Aminosäuren, Archäen, Bakterien, Baum des Lebens, Bedeutung, Bedeutung - abstraktes Konstrukt, Chaitin, Chiralität, Cyanobakterien, Darwin, Davies, Dekodieren, DNA als Programm, DNA-Molekül, Eukaryoten, Gedächtnis, gen, Genom, Gödel, Information, Interpretation, Kode, kodieren, Kodierung, Leben - Ursprung und Bedeutung, Lernen, mRNA, Mutation, Photosynthese, Proteine, Replikation, Reproduktion - biologische, Ribosom, Semantik, Sequenzierung, Speichern, Stammbaum, Stromatolythen, Symbiose, tRNA, Turing, Turing Maschine - chemisch implementiert, Urey-Miller-Experiment, Vorfahren, Vorläufer, Zeichen, Zeichenbenutzer, Zeichenmaterialcagent

Paul Davies, The FIFTH MIRACLE: The Search for the Origin and Meaning of Life, New York:1999, Simon & Schuster

Fortsetzung von Suche… (Teil 1)

Start: 27.Aug.2012

Letzte Fortsetzung: 1.Sept.2012

Das dritte Kapitel ist überschrieben ‚Out of the Slime‘. (SS.69-96) Es startet mit Überlegungen zur Linie der Vorfahren (Stammbaum), die alle auf ‚gemeinsame Vorfahren‘ zurückführen. Für uns Menschen zu den ersten Exemplaren des homo sapiens in Afrika vor 100.000 Jahren, zu den einige Millionen Jahre zurückliegenden gemeinsamen Vorläufern von Affen und Menschen; ca. 500 Mio Jahre früher waren die Vorläufer Fische, zwei Milliarden Jahre zurück waren es Mikroben. Und diese Rückführung betrifft alle bekannten Lebensformen, die, je weiter zurück, sich immer mehr in gemeinsamen Vorläufern vereinigen, bis hin zu den Vorläufern allen irdischen Lebens, Mikroorganismen, Bakterien, die die ersten waren.(vgl. S.69f)
[Anmerkung: Die Formulierung von einem ‚einzelnen hominiden Vorfahren‘ oder gar von der ‚afrikanischen Eva‘ kann den Eindruck erwecken, als ob der erste gemeinsame Vorfahre ein einzelnes Individuum war. Das scheint mir aber irreführend. Bedenkt man, dass wir ‚Übergangsphasen‘ haben von Atomen zu Molekülen, von Molekülen zu Netzwerken von Molekülen, von Molekülnetzwerken zu Zellen, usw. dann waren diese Übergänge nur erfolgreich, weil viele Milliarden und Abermilliarden von Elementen ‚gleichzeitig‘ beteiligt waren; anders wäre ein ‚Überleben‘ unter widrigsten Umständen überhaupt nicht möglich gewesen. Und es spricht alles dafür, dass dieses ‚Prinzip der Homogenität‘ sich auch bei den ‚komplexeren‘ Entwicklungsstufen fortgesetzt hat. Ein einzelnes Exemplar einer Art, das durch irgendwelche besonderen Eigenschaften ‚aus der Reihe‘ gefallen wäre, hätte gar nicht existieren können. Es braucht immer eine Vielzahl von hinreichend ‚ähnlichen‘ Exemplaren, dass ein Zusammenwirken und Fortbestehen realisiert werden kann. Die ‚Vorgänger‘ sind also eher keine spezifischen Individuen (wenngleich in direkter Abstammung schon), sondern immer Individuen als Mitglieder einer bestimmten ‚Art‘.]
Es ist überliefert, dass Darwin im Sommer 1837, nach der Rückkehr von seiner Forschungsreise mit der HMS Beagle in seinem Notizbuch erstmalig einen irregulär verzweigenden Baum gemalt hat, um die vermuteten genealogischen Zusammenhänge der verschiedenen Arten darzustellen. Der Baum kodierte die Annahme, dass letztlich alle bekannten Lebensformen auf einen gemeinsamen Ursprung zurückgehen. Ferner wird deutlich, dass viele Arten (heutige Schätzungen: 99%) irgendwann ‚ausgestorben‘ sind. Im Falle einzelliger Lebewesen gab es aber – wie wir heute zunehmend erkennen können – auch das Phänomene der Symbiose: ein Mikroorganismus ‚frißt‘ andere und ‚integriert‘ deren Leistung ‚in sich‘ (Beispiel die Mitochondrien als Teil der heute bekannten Zellen). Dies bedeutet, dass ‚Aussterben‘ auch als ‚Synthese‘ auftreten kann.(vgl. SS.70-75)
Die Argumente für den Zusammenhang auf Zellebene zwischen allen bekannten und ausgestorbenen Arten mit gemeinsamen Vorläufern beruhen auf den empirischen Fakten, z.B. dass die metabolischen Verläufe der einzelnen Zellen gleich sind, dass die Art und Weise der genetischen Kodierung und Weitergabe gleich ist, dass der genetische Kode im Detail der gleiche ist, oder ein kurioses Detail wie die molekulare Ausrichtung – bekannt als Chiralität –; obgleich jedes Molekül aufgrund der geltenden Gesetze sowohl rechts- oder linkshändig sein kann, ist die DNA bei allen Zellen ‚rechtshändig‘ und ihr Spiegelbild linkshändig. (vgl.SS.71-73)
Da das DNA-Molekül bei allen bekannten Lebensformen in gleicher Weise unter Benutzung von Bausteinen aus Aminosäure kodiert ist, kann man diese Moleküle mit modernen Sequenzierungstechniken Element für Element vergleichen. Unter der generellen Annahme, dass sich bei Weitergabe der Erbinformationen durch zufällige Mutationen von Generation zur Generation Änderungen ergeben können, kann man anhand der Anzahl der verschiedenen Elemente sowohl einen ‚genetischen Unterschied‘ wie auch einen ‚genealogischen Abstand‘ konstruieren. Der genetische Unterschied ist direkt ’sichtbar‘, die genaue Bestimmung des genealogischen Abstands im ‚Stammbaum‘ hängt zusätzlich ab von der ‚Veränderungsgeschwindigkeit‘. Im Jahr 1999 war die Faktenlage so, dass man annimmt, dass es gemeinsame Vorläufer für alles Leben gegeben hat, die sich vor ca. 3 Milliarden Jahren in die Art ‚Bakterien‘ und ‚Nicht-Bakterien‘ verzweigt haben. Die Nicht-Bakterien haben sich dann weiter verzweigt in ‚Eukaryoten‘ und ‚Archäen‘. (vgl. SS.75-79)
Davies berichtet von bio-geologischen Funden nach denen in de Nähe von Isua (Grönland) Felsen von vor mindestens -3.85 Milliarden Jahren gefunden wurden mit Spuren von Bakterien. Ebenso gibt es Funde von Stromatolythen (Nähe Shark Bay, Australien), mit Anzeichen für Cyanobakterien aus der Zeit von ca. -3.5 Milliarden Jahren und aus der gleichen Zeit Mikrofossilien in den Warrawoona Bergen (Australien). Nach den Ergebnissen aus 1999 hatten die Cyanobakterien schon -3.5 Mrd. Jahre Mechanismen für Photosynthese, einem höchst komplexen Prozess.(vgl. SS.79-81)
Die immer weitere Zurückverlagerung von Mikroorganismen in die Vergangenheit löste aber nicht das Problem der Entstehung dieser komplexen Strukturen. Entgegen der früher verbreiteten Anschauung, dass ‚Leben‘ nicht aus ‚toter Materie‘ entstehen kann, hatte schon Darwin 1871 in einem Brief die Überlegung geäußert, dass in einer geeigneten chemischen Lösung über einen hinreichend langen Zeitraum jene Moleküle und Molekülvernetzungen entstehen könnten, die dann zu den bekannten Lebensformen führen. Aber erst in den 20iger Jahren des 20.Jahrhunderts waren es Alexander Oparin (Rußland) und J.B.S.Haldane (England) die diese Überlegungen ernst nahmen. Statt einem kleinen See, wie bei Darwin, nahm Haldane an, dass es die Ozeane waren, die den Raum für den Übergangsprozess von ‚Materie‘ zu ‚Leben‘ boten. Beiden Forschern fehlten aber in ihrer Zeit die entscheidende Werkzeuge und Erkenntnisse der Biochemie und Molekularbiologie, um ihre Hypothesen testen zu können. Es war Harold Urey (USA) vorbehalten, 1953 mit ersten Laborexperimenten beginnen zu können, um die Hypothesen zu testen. (vgl. SS.81-86)
Mit Hilfe des Studenten Miller arrangierte Urey ein Experiment, bei dem im Glaskolben eine ‚Mini-Erde‘ bestehend aus etwas Wasser mit den Gasen Methan, Hydrogen und Ammonium angesetzt wurde. Laut Annahme sollte dies der Situation um ca. -4 Millarden Jahren entsprechen. Miller erzeugte dann in dem Glaskolben elektrische Funken, um den Effekt von Sonnenlicht zu simulieren. Nach einer Woche fand er dann verschiedene Amino-Säuren, die als Bausteine in allen biologischen Strukturen vorkommen, speziell auch in Proteinen.(vgl. S.86f)
Die Begeisterung war groß. Nachfolgende Überlegungen machten dann aber klar, dass damit noch nicht viel erreicht war. Die Erkenntnisse der Geologen deuteten in den nachfolgenden Jahren eher dahin, dass die Erdatmosphäre, die die sich mehrfach geändert hatte, kaum Ammonium und Methan enthielt, sondern eher reaktions-neutrales Kohlendioxyd und Schwefel, Gase die keine Aminosäuren produzieren. (vgl.S.87)
Darüber hinaus ist mit dem Auftreten von Aminosäuren als Bausteine für mögliche größere Moleküle noch nichts darüber gesagt, ob und wie diese größere Moleküle entstehen können. Genauso wenig wie ein Haufen Ziegelsteine einfach so ein geordnetes Haus bilden wird, genauso wenig formen einzelne Aminosäuren ‚einfach so‘ ein komplexes Molekül (ein Peptid oder Polypeptid). Dazu muss der zweite Hauptsatz überwunden werden, nach dem ’spontane‘ Prozesse nur in Richtung Energieabbau ablaufen. Will man dagegen komplexe Moleküle bauen, muss man gegen den zweiten Hauptsatz die Energie erhöhen; dies muss gezielt geschehen. In einem angenommenen Ozean ist dies extrem unwahrscheinlich, da hier Verbindungen eher aufgelöst statt synthetisiert werden.(vgl.87-90)
Der Chemiker Sidney Fox erweiterte das Urey-Experiment durch Zufuhr von Wärme. In der Tat bildeten sich dann Ketten von Aminosäurebausteinen die er ‚Proteinoide‘ nannte. Diese waren eine Mischung aus links- und rechts-händigen Molekülen, während die biologisch relevanten Moleküle alle links-händig sind. Mehr noch, die biologisch relevanten Aminosäureketten sind hochspezialisiert. Aus der ungeheuren Zahl möglicher Kombinationen die ‚richtigen‘ per Zufall zu treffen grenzt mathematisch ans Unmögliche.(vgl.S.90f) Dazu kommt, dass eine Zelle viele verschiedene komplexe Moleküle benötigt (neben Proteinen auch Lipide, Nukleinsäuren, Ribosomen usw.). Nicht nur ist jedes dieser Moleküle hochkomplex, sondern sie entfalten ihre spezifische Wirkung als ‚lebendiges Ensemble‘ erst im Zusammenspiel. Jedes Molekül ‚für sich‘ weiß aber nichts von einem Zusammenhang. Wo kommen die Informationen für den Zusammenhang her? (vgl.S.91f) Rein mathematisch ist die Wahrscheinlichkeit, dass sich die ‚richtigen‘ Proteine bilden in der Größenordnung von 1:10^40000, oder, um ein eindrucksvolles Bild des Physikers Fred Hoyle zu benutzen: genauso unwahrscheinlich, wie wenn ein Wirbelsturm aus einem Schrottplatz eine voll funktionsfähige Boeing 747 erzeugen würde. (vgl.S.95)
Die Versuchung, das Phänomen des Lebens angesichts dieser extremen Unwahrscheinlichkeiten als etwas ‚Besonderes‘, als einen extrem glücklichen Zufall, zu charakterisieren, ist groß. Davies plädiert für eine Erklärung als eines ’natürlichen physikalischen Prozesses‘. (S.95f)
Im Kapitel 4 ‚The Message in the Machine‘ (SS.97-122) versucht Davies mögliche naturwissenschaftliche Erklärungsansätze, beginnend bei den Molekülen, vorzustellen. Die Zelle selbst ist so ungeheuerlich komplex, dass noch ein Niels Bohr die Meinung vertrat, dass Leben als ein unerklärbares Faktum hinzunehmen sei (vgl.Anmk.1,S.99). Für die Rekonstruktion erinnert Davies nochmals daran, dass diejenigen Eigenschaften, die ‚lebende‘ Systeme von ’nicht-lebenden‘ Systemen auszeichnen, Makroeigenschaften sind, die sich nicht allein durch Verweis auf die einzelnen Bestandteile erklären lassen, sondern nur und ausschließlich durch das Zusammenspiel der einzelnen Komponenten. Zentrale Eigenschaft ist hier die Reproduktion. (vgl.SS.97-99)
Reproduktion ist im Kern gebunden an das Kopieren von drei-dimensional charakterisierten DNA-Molekülen. Vereinfacht besteht solch ein DNA-Molekül aus zwei komplementären Strängen, die über eine vierelementiges Alphabet von Nukleinsäurebasen miteinander so verbunden sind, dass es zu jeder Nukleinsäurebase genau ein passendes Gegenstück gibt. Fehlt ein Gegenstück, ist es bei Kenntnis des Kodes einfach, das andere Stück zu ergänzen. Ketten von den vierelementigen Basen können ‚Wörter‘ bilden, die ‚genetische Informationen‘ kodieren. Ein ‚Gen‘ wäre dann solch ein ‚Basen-Wort‘. Und das ganze Molekül wäre dann die Summe aller Gene als ‚Genom‘. Das ‚Auftrennen‘ von Doppelsträngen zum Zwecke des Kopierens wie auch das wieder ‚Zusammenfügen‘ besorgen spezialisierte andere Moleküle (Enzyme). Insgesamt kann es beim Auftrennen, Kopieren und wieder Zusammenfügen zu ‚Fehlern‘ (Mutationen) kommen. (vgl.SS.100-104)
Da DNA-Moleküle als solche nicht handlungsfähig sind benötigen sie eine Umgebung, die dafür Sorge trägt, dass die genetischen Informationen gesichert und weitergegeben werden. Im einfachen Fall ist dies eine Zelle. Um eine Zelle aufzubauen benötigt man Proteine als Baumaterial und als Enzyme. Proteine werden mithilfe der genetischen Informationen in der DNA erzeugt. Dazu wird eine Kopie der DNA-Informationen in ein Molekül genannt Boten-RNA (messenger RNA, mRNA) kopiert, dieses wandert zu einem komplexen Molekülnetzwerk genannt ‚Ribosom‘. Ribosomen ‚lesen‘ ein mRNA-Molekül als ‚Bauanleitung‘ und generieren anhand dieser Informationen Proteine, die aus einem Alphabet von 20 (bisweilen 21) Aminosäuren zusammengesetzt werden. Die Aminosäuren, die mithilfe des Ribosoms Stück für Stück aneinandergereiht werden, werden von spezialisierten Transportmolekülen (transfer RNA, tRNA) ‚gebracht‘, die so gebaut sind, dass immer nur dasjenige tRNA-Molekül andocken kann, das zur jeweiligen mRNA-Information ‚passt‘. Sobald die mRNA-Information ‚abgearbeitet‘ ist, liegt eines von vielen zehntausend möglichen Proteinen vor. (vgl.SS. 104-107) Bemerkenswert ist die ‚Dualität‘ der DNA-Moleküle (wie auch der mRNA) sowohl als ‚Material/ Hardware‘ wie auch als ‚Information/ Software‘. (vgl.S.108)
Diese ‚digitale‘ Perspektive vertieft Davies durch weitere Betrachtung und führt den Leser zu einem Punkt, bei dem man den Eindruck gewinnt, dass die beobachtbaren und messbaren Materialien letztlich austauschbar sind bezogen auf die ‚impliziten Strukturen‘, die damit realisiert werden. Am Beispiel eines Modellflugzeugs, das mittels Radiowellen ferngesteuert wird, baut er eine Analogie dahingehend auf, dass die Hardware (das Material) des Flugzeugs wie auch der Radiowellen selbst als solche nicht erklären, was das Flugzeug tut. Die Hardware ermöglicht zwar grundsätzlich bestimmte Flugeigenschaften, aber ob und wie diese Eigenschaften genutzt werden, das wird durch ‚Informationen‘ bestimmt, die per Radiowellen von einem Sender/ Empfänger kommuniziert werden. Im Fall einer Zelle bilden komplexe Molekülnetzwerke die Hardware mit bestimmten verfügbaren chemischen Eigenschaften, aber ihr Gesamtverhalten wird gesteuert durch Informationen, die primär im DNA-Molekül kodiert vorliegt und die als ‚dekodierte‘ Information alles steuert.(vgl. SS.113-115)
[Anmerkung: Wie schon zuvor festgestellt, repräsentieren Atome und Moleküle als solche keine ‚Information‘ ‚von sich aus‘. Sie bilden mögliche ‚Ereignisse‘ E ‚für andere‘ Strukturen S, sofern diese andere Strukturen S auf irgendeine Weise von E ‚beeinflusst‘ werden können. Rein physikalisch (und chemisch) gibt es unterschiedliche Einwirkungsmöglichkeiten (z.B. elektrische Ladungen, Gravitation,…). Im Falle der ‚Information‘ sind es aber nicht nur solche primären physikalisch-chemischen Eigenschaften, die benutzt werden, sondern das ‚empfangende‘ System S befindet sich in einem Zustand, S_inf, der es dem System ermöglicht, bestimmte physikalisch-chemische Ereignisse E als ‚Elemente eines Kodes‘ zu ‚interpretieren. Ein Kode ist minimal eine Abbildungsvorschrift, die Elemente einer Menge X (die primäre Ereignismenge) in eine Bildmenge Y (irgendwelche anderen Ereignisse, die Bedeutung) ‚übersetzt‘ (kodiert), also CODE: X —> Y. Das Materiell-Stoffliche wird damit zum ‚Träger von Informationen‘, zu einem ‚Zeichen‘, das von einem Empfänger S ‚verstanden‘ wird. Im Falle der zuvor geschilderten Replikation wurden ausgehend von einem DNA-Molekül (= X, Ereignis, Zeichen) mittels mRNA, tRNA und Ribosom (= Kode, CODE) bestimmte Proteine (=Y, Bedeutung) erzeugt. Dies bedeutet, dass die erzeugten Proteine die ‚Bedeutung des DNA-Moleküls‘ sind unter Voraussetzung eines ‚existierenden Kodes‘ realisiert im Zusammenspiel eines Netzwerkes von mRNA, tRNAs und Ribosom. Das Paradoxe daran ist, das die einzelnen Bestandteile des Kodes, die Moleküle mRNA, tRNA und Ribosom (letzteres selber hochkomplex) ‚für sich genommen‘ keinen Kode darstellen, nur in dem spezifischen Zusammenspiel! Wenn also die einzelnen materiellen Bestandteile, die Atome und Moleküle ‚für sich gesehen‘ keinen komplexen Kode darstellen, woher kommt dann die Information, die alle diese materiell hochkomplexen Bestandteile auf eine Weise ‚zusammenspielen‘ lässt, die weit über das hinausgeht, was die Bestandteile einzeln ‚verkörpern‘? ]
zelle_tm

[Anmerkung: Es gibt noch eine andere interssante Perspektive. Das mit Abstand wichtigste Konzept in der (theoretischen) Informatik ist das Konzept der Berechenbarkeit, wie es zunächst von Goedel 1931, dann von Turing in seinem berühmten Artikel von 1936-7 vorgelegt worden ist. In seinem Artikel definiert Turing das mathematische (!) Konzept einer Vorrichtung, die alle denkbaren berechenbaren Prozesse beschreiben soll. Später gaben andere dieser Vorrichtung den Namen ‚Turingmaschine‘ und bis heute haben alle Beweise immer nur dies eine gezeigt, dass es kein anderes formales Konzept der intuitiven ‚Berechenbarkeit‘ gibt, das ’stärker‘ ist als das der Turingmaschine. Die Turingmaschine ist damit einer der wichtigsten – wenn nicht überhaupt der wichtigste — philosophischen Begriff(e). Viele verbinden den Begriff der Turingmaschine oft mit den heute bekannten Computern oder sehen darin die Beschreibung eines konkreten, wenngleich sehr ‚umständlichen‘ Computers. Das ist aber vollständig an der Sache vorbei. Die Turingmaschine ist weder ein konkreter Computer noch überhaupt etwas Konkretes. Genau wie der mathematische Begriff der natürlichen Zahlen ein mathematisches Konzept ist, das aufgrund der ihm innewohnenden endlichen Unendlichkeit niemals eine reale Zahlenmenge beschreibt, sondern nur das mathematische Konzept einer endlich-unendlichen Menge von abstrakten Objekten, für die die Zahlen des Alltags ‚Beispiele‘ sind, genauso ist auch das Konzept der Turingmaschine ein rein abstraktes Gebilde, für das man konkrete Beispiele angeben kann, die aber das mathematische Konzept selbst nie erschöpfen (die Turingmaschine hat z.B. ein unendliches Schreib-Lese-Band, etwas, das niemals real existieren kann).
]
[Anmerkung: Das Interessante ist nun, dass man z.B. die Funktion des Ribosoms strukturell mit dem Konzept einer Turingmaschine beschreiben kann (vgl. Bild). Das Ribosom ist jene Funktionseinheit von Molekülen, die einen Input bestehend aus mRNA und tRNAs überführen kann in einen Output bestehend aus einem Protein. Dies ist nur möglich, weil das Ribosom die mRNA als Kette von Informationseinheiten ‚interpretiert‘ (dekodiert), die dazu führen, dass bestimmte tRNA-Einheiten zu einem Protein zusammengebaut werden. Mathematisch kann man diese funktionelle Verhalten eines Ribosoms daher als ein ‚Programm‘ beschreiben, das gleichbedeutend ist mit einer ‚Funktion‘ bzw. Abbildungsvorschrift der Art ‚RIBOSOM: mRNA x tRNA —> PROTEIN. Das Ribosom stellt somit eine chemische Variante einer Turingmaschine dar (statt digitalen Chips oder Neuronen). Bleibt die Frage, wie es zur ‚Ausbildung‘ eines Ribosoms kommen kann, das ’synchron‘ zu entsprechenden mRNA-Molekülen die richtige Abbildungsvorschrift besitzt.
]
Eine andere Blickweise auf das Phänomen der Information ist jene des Mathematikers Chaitin, der darauf aufmerksam gemacht hat, dass man das ‚Programm‘ eines Computers (sein Algorithmus, seine Abbildungsfunktion, seine Dekodierungsfunktion…) auch als eine Zeichenkette auffassen kann, die nur aus Einsen und Nullen besteht (also ‚1101001101010..‘). Je mehr Wiederholungen solch eine Zeichenkette enthalten würde, um so mehr Redundanz würde sie enthalten. Je weniger Wiederholung, um so weniger Redundanz, um so höher die ‚Informationsdichte‘. In einer Zeichenkette ohne jegliche Redundanz wäre jedes einzelne Zeichen wichtig. Solche Zeichenketten sind formal nicht mehr von reinen zufallsbedingten Ketten unterscheidbar. Dennoch haben biologisch nicht alle zufälligen Ketten eine ’nützliche‘ Bedeutung. DNA-Moleküle ( bzw. deren Komplement die jeweiligen mRNA-Moleküle) kann man wegen ihrer Funktion als ‚Befehlssequenzen‘ als solche binär kodierten Programme auffassen. DNA-Moleküle können also durch Zufall erzeugt worden sein, aber nicht alle zufälligen Erzeugungen sind ’nützlich‘, nur ein verschwindend geringer Teil. Dass die ‚Natur‘ es geschafft hat, aus der unendlichen Menge der nicht-nützlichen Moleküle per Zufall die herauszufischen, die ’nützlich‘ sind, geschah einmal durch das Zusammenspiel von Zufall in Gestalt von ‚Mutation‘ sowie Auswahl der ‚Nützlichen‘ durch Selektion. Es stellt sich die Frage, ob diese Randbedingungen ausreichen, um das hohe Mass an Unwahrscheinlichkeit zu überwinden. (vgl. SS. 119-122)
[Anmerkung: Im Falle ‚lernender‘ Systeme S_learn haben wir den Fall, dass diese Systeme einen ‚Kode‘ ‚lernen‘ können, weil sie in der Lage sind, Ereignisse in bestimmter Weise zu ‚bearbeiten‘ und zu ’speichern‘, d.h. sie haben Speichersysteme, Gedächtnisse (Memory), die dies ermöglichen. Jedes Kind kann ‚lernen‘, welche Ereignisse welche Wirkung haben und z.B. welche Worte was bedeuten. Ein Gedächtnis ist eine Art ‚Metasystem‘, in dem sich ‚wahrnehmbare‘ Ereignisse E in einer abgeleiteten Form E^+ so speichern (= spiegeln) lassen, dass mit dieser abgeleiteten Form E^+ ‚gearbeitet‘ werden kann. Dies setzt voraus, dass es mindestens zwei verschiedene ‚Ebenen‘ (layer, level) im Gedächtnis gibt: die ‚primären Ereignisse‘ E^+ sowie die möglichen ‚Beziehungen‘ RE, innerhalb deren diese vorkommen. Ohne dieses ‚Beziehungswissen‘ gibt es nur isolierte Ereignisse. Im Falle multizellulärer Organismen wird diese Speicheraufgabe durch ein Netzwerk von neuronalen Zellen (Gehirn, Brain) realisiert. Der einzelnen Zelle kann man nicht ansehen, welche Funktion sie hat; nur im Zusammenwirken von vielen Zellen ergeben sich bestimmte Funktionen, wie z.B. die ‚Bearbeitung‘ sensorischer Signale oder das ‚Speichern‘ oder die Einordnung in eine ‚Beziehung‘. Sieht man mal von der spannenden Frage ab, wie es zur Ausbildung eines so komplexen Netzwerkes von Neuronen kommen konnte, ohne dass ein einzelnes Neuron als solches ‚irgend etwas weiß‘, dann stellt sich die Frage, auf welche Weise Netzwerke von Molekülen ‚lernen‘ können. Eine minimale Form von Lernen wäre das ‚Bewahren‘ eines Zustandes E^+, der durch ein anderes Ereignis E ausgelöst wurde; zusätzlich müsste es ein ‚Bewahren‘ von Zuständen geben, die Relationen RE zwischen primären Zuständen E^+ ‚bewahren‘. Solange wir es mit frei beweglichen Molekülen zu tun haben, ist kaum zu sehen, wie es zu solchen ‚Bewahrungs-‚ sprich ‚Speicherereignissen‘ kommen kann. Sollte es in irgend einer Weise Raumgebiete geben, die über eine ‚hinreichend lange Zeit‘ ‚konstant bleiben, dann wäre es zumindest im Prinzip möglich, dass solche ‚Bewahrungsereignisse‘ stattfinden. Andererseits muss man aber auch sehen, dass diese ‚Bewahrungsereignisse‘ aus Sicht eines möglichen Kodes nur möglich sind, wenn die realisierenden Materialien – hier die Moleküle bzw. Vorstufen zu diesen – physikalisch-chemische Eigenschaften aufweisen, die grundsätzlich solche Prozesse nicht nur ermöglichen, sondern tendenziell auch ‚begünstigen‘, und dies unter Berücksichtigung, dass diese Prozesse ‚entgegen der Entropie‘ wirken müssen. Dies bedeutet, dass — will man keine ‚magischen Kräfte‘ annehmen — diese Reaktionspotentiale schon in den physikalisch-chemischen Materialien ‚angelegt‘ sein müssen, damit sie überhaupt auftreten können. Weder Energie entsteht aus dem Nichts noch – wie wir hier annehmen – Information. Wenn wir also sagen müssen, dass sämtliche bekannte Materie nur eine andere Zustandsform von Energie ist, dann müssen wir vielleicht auch annehmen, dass alle bekannten ‚Kodes‘ im Universum nichts anderes sind als eine andere Form derjenigen Information, die von vornherein in der Energie ‚enthalten‘ ist. Genauso wie Atome und die subatomaren Teilchen nicht ’neutral‘ sind sondern von vornherein nur mit charakteristischen (messbaren) Eigenschaften auftreten, genauso müsste man dann annehmen, dass die komplexen Kodes, die wir in der Welt und dann vor allem am Beispiel biologischer Systeme bestaunen können, ihre Wurzeln in der grundsätzlichen ‚Informiertheit‘ aller Materie hat. Atome formieren zu Molekülen, weil die physikalischen Eigenschaften sie dazu ‚bewegen‘. Molkülnetzwerke entfalten ein spezifisches ‚Zusammenspiel‘, weil ihre physikalischen Eigenschaften das ‚Wahrnehmen‘, ‚Speichern‘ und ‚Dekodieren‘ von Ereignissen E in einem anderen System S grundsätzlich ermöglichen und begünstigen. Mit dieser Annahme verschwindet ‚dunkle Magie‘ und die Phänomene werden ‚transparent‘, ‚messbar‘, ‚manipulierbar‘, ‚reproduzierbar‘. Und noch mehr: das bisherige physikalische Universum erscheint in einem völlig neuen Licht. Die bekannte Materie verkörpert neben den bislang bekannten physikalisch-chemischen Eigenschaften auch ‚Information‘ von ungeheuerlichen Ausmaßen. Und diese Information ‚bricht sich selbst Bahn‘, sie ‚zeigt‘ sich in Gestalt des Biologischen. Das ‚Wesen‘ des Biologischen sind dann nicht die ‚Zellen als Material‘, das Blut, die Muskeln, die Energieversorgung usw., sondern die Fähigkeit, immer komplexer Informationen aus dem Universum ‚heraus zu ziehen, aufzubereiten, verfügbar zu machen, und damit das ‚innere Gesicht‘ des Universums sichtbar zu machen. Somit wird ‚Wissen‘ und ‚Wissenschaft‘ zur zentralen Eigenschaft des Universums samt den dazugehörigen Kommunikationsmechanismen.]
Fortsetzung Teil 3

Einen Überblick über alle bisherigen Themen findet sich HIER

Zitierte Literatur:

Chaitin, G.J. Information, Randomness & Incompleteness, 2nd ed., World Scientific, 1990

Turing, A. M. On Computable Numbers with an Application to the Entscheidungsproblem. In: Proc. London Math. Soc., Ser.2, vol.42(1936), pp.230-265; received May 25, 1936; Appendix added August 28; read November 12, 1936; corr. Ibid. vol.43(1937), pp.544-546. Turing’s paper appeared in Part 2 of vol.42 which was issued in December 1936 (Reprint in M.DAVIS 1965, pp.116-151; corr. ibid. pp.151-154).

Interessante Links:

Ein Video in Youtube, das eine Rede von Pauls Davies dokumentiert, die thematisch zur Buchbesprechung passt und ihn als Person etwas erkennbar macht.

Teil 1:
http://www.youtube.com/watch?v=9tB1jppI3fo

Teil 2:
http://www.youtube.com/watch?v=DXXFNnmgcVs

Teil 3:
http://www.youtube.com/watch?v=Ok9APrXfIOU

Teil 4:
http://www.youtube.com/watch?v=vXqqa1_0i7E

Part 5:
http://www.youtube.com/watch?v=QVrRL3u0dF4
Es gibt noch einige andere Videos mit Paul Davies bei Youtube.

SUCHE NACH DEM URSPRUNG UND DER BEDEUTUNG DES LEBENS. Reflexionen zum Buch von Paul Davies “The fifth Miracle”

21. August 2012Allgemein, Astrobiologie, Bedeutung, Bedeutungsmaterial, Big-Bang Theorie, Biogenese, Brownlee, Computer - chemischer, DNA-Molekül, Eigen - Manfred, Energie, Energie - freie, Energie Zustandsformen, Entropie, Entropie - negative, Evolution - chemische, Fehler, Fehler - biologische, Fehlervermeidung, Gale, Genesis - Kap.1, Gravitation, Hintergrundstrahlung, Information, Leben, Leben - Ursprung und Bedeutung, Maschine - semiotische, Negentropie, Objekte - informationsgetriebene, Ordnung, Rauchfuß, Replikation, Schroedinger, Semantik, Semiotik, Semiotische Maschine, Thermpodynamik - zweiter Hauptsatz, Turing Maschine - chemisch implementiert, Universum - lebensfreundliches, Unordnung, Vervielfältigung - biologisch, Wardcagent