Archiv der Kategorie: Semantik

MEMO PHILOSOPHIE JETZT – WERKSTATTGESPRÄCH – 27.November 2016

Antike Philosophie, Aristoteles, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsmaterial, Mittelalter, Philosophie, Philosophie des Mittelalters, Philosophiewerkstatt, Philosophiewerkstatt, Semantik, Sprache, Sprachliche Äußerung, Sprachmaterial, Sprachspiel, Sprecher, Werkstattgespräch, Zeichen, Zeichenbenutzer, Zeichenmaterial

EINLADUNG

  1. Entsprechend der Einladung war das Thema dieses Treffens dieses Mal nicht das Fühlen (im philosophischen Sinne), sondern das Denken, unser eigenes Denken.

EINSTIMMUNG

  1. Jeden Tag benutzen wir unser Denken, indem wir mit anderen direkt kommunizieren oder indem wir jemandem etwas schreiben oder von jemand anderem etwas lesen/ hören.
  2. Aber was tun wir da, wenn wir mit anderen direkt kommunizieren?
  3. Die Frage ist nicht neu und hat schon viele Menschen vor uns bewegt.
  4. In einem kleinen historischen Blitzlicht wurde anhand wichtiger Philosophen und Denkern ein Zeitstrahl eingeblendet, der von Platos Geburt bis zur Gegenwart reichte (siehe Bild 1).
Zeittaffel von Plato bis zur Gegenwart
BILD 1: Zeittaffel von Plato bis zur Gegenwart
  1. Aus der Breite der (antiken) griechischen Philosophie waren stellvertretend nur die Namen der beiden bekanntesten griechischen Denker Plato und Aristoteles angeführt. Es dauerte ca. 600 – 800 Jahre, bis einige wenige Werke von Aristoteles im römischen Reich eine Übersetzung fanden, die bis ins Mittelalter wirkten.
  2. Im Mittelalter – hier abgebildet in der Spanne zwischen ca. 735 und 1360, also ca. 600 Jahre – gab es erst die Phase der direkten Aufnahme der wenigen aristotelischen Texte (zusammen mit Werken von Porphyr, Victorinus und Boethius); aus der intensiven Kommentierung entstanden zunehmend eigene, neue Positionen, die am Ende des 14.Jahrhunderts zu dem führte, was dann später neue empirische Wissenschaft, neue Logik und Mathematik bzw. neue Philosophie genannt wurde.
  3. Der Überblick machte dann einen Sprung in die letzten 150 Jahre bis zur Gegenwart.
  4. Der Überblick beginnt mit Bréal, der als Begründer der Idee einer Semantik gilt, der Lehre von der sprachlichen Bedeutung. Aus der Vielzahl der hier einschlägigen Denker und Denkerinnen folgt eine Auswahl der besonders bekannten Namen (teilweise mit Angabe der hier einschlägigen Werke).
  5. Allerdings, wie neuere Studien zum Mittelalter zeigen, sind viele der Ideen, die heute als neu daher kommen, im Mittelalter zumindest angedacht worden. Während im neuzeitlichen Denken des 20.Jahrhunderts die formalen Aspekte des Denkens und Sprechens stark bis fast vollständig von den assoziierten Inhalten (Bedeutungen) losgelöst erscheinen, hat das Mittelalter noch versucht, die Ausdrucksstrukturen und die Logik in ihrer intensiven Wechselwirkung zu denken. So sind z.B. die google-Algorithmen zur Analyse von Texten (und Bildern und …) heute ausschließlich an den formalen Ausdruckselementen orientiert; ein Bezug zu assoziierten Bedeutungen, wie sie jeder normale Sprecher-Hörer benutzt, fehlt vollständig. Dieser Bezug ist mit den bekannten Algorithmen auch nicht zu bekommen.
  6. Nach dieser blitzlichtartigen Einbettung der aktuellen Situation in den übergreifenden Denkkontext gab es die ‚individuelle Fühlpause‘ (manche nennen dies Meditation). Jeder konnte für sich – wie auch immer – 20 Min meditieren und sich anschließend Notizen machen.
  7. Wir stiegen dann in die erste Diskursrunde ein.(Siehe Bild 2)
PhJ Werkstattgespraech 27.November 2016 im INM - Gedankenskizze
BILD 2: PhJ Werkstattgespraech 27.November 2016 im INM – Gedankenskizze

START MIT EINER ÄUSSERUNG

  1. Für das gemeinsame Gedankenexperiment gab es zwei Leitfragen, von denen wir letztlich nur die erste ansatzweise bearbeiten konnten: FRAGE1: WIE HÄNGT EIN SPRACHLICHER AUSDRUCK MIT SEINER BEDEUTUNG ZUSAMMEN?
  2. Das Experiment begann damit, dass ein Teilnehmer aus der Runde spontan eine Äußerung macht: „Es ist behaglich“.
  3. Anhand dieser sprachlichen Äußerung entwickelte sich ein lebhaftes und intensives Gespräch, in dem jeder immer neue Aspekte beisteuerte.
  4. Wie man aus dem Bild 2 entnehmen kann, gab es zunächst mal Äußerungen von anderen TeilnehmernInnen, wie man diese anderen es formuliert hätten (siehe Bild 2).
  5. Daraus ergab sich, dass eine aktuelle, konkrete Äußerung in Beziehung zu setzen ist zum jeweiligen Sprecher bzw. Hörer. Je nach Sprecher empfindet dieser den Raum mit seiner für alle gleichen Temperatur entweder zu warm (also nicht behaglich), gerade richtig (z.B. behaglich) oder ganz anders.
  6. Außerdem empfanden manche Teilnehmer als Hörer die Allgemeinheit des Ausdrucks („Es ist“) zu vage. Lieber hätten sie gehört, dass der Sprecher das konkreter sagt, mehr über sich selbst („Ich empfinde es…“), was dem Hörer eher die Möglichkeit gibt, die Situation einzuschätzen. In der allgemeinen, unbestimmten Formulierung konnte es klingen, als ob der Sprecher für sich in Anspruch nimmt, auch für die anderen zu sprechen. Das fordert evtl. Widerspruch heraus…
  7. Dann wurde darauf aufmerksam gemacht, dass die Art der sprachlichen Äußerungen unterschiedliche Muster zulässt. Neben sachlicher Feststellung/ Behauptung gibt es auch einfache Ausrufe, Fragen, Befehle, Versprechen usw.
  8. Weitere Aspekte kamen ins Spiel: die Körpersprache des Sprechers. Wie steht diese im Verhältnis zu dem, was er sagt.
  9. Mit Beispielen aus eigenen Sprecherfahrungen wurde thematisiert, wie jemand von ganz vielen verschiedenen Gewohnheiten, Regeln, gesellschaftlichen Erwartungen in seinen Äußerungen gesteuert sein kann. Der Begriff der Rolle wurde eingeführt. Die Gesamtheit der wirkenden Regeln und Erwartungen können in der jeweiligen Situationen normativ wirken: jemand hat in einer bestimmten Situation bestimmte Gefühle, muss aber als Elternteil in diesem Moment eine gewisse Verantwortung wahrnehmen, entsprechend ein Therapeut in einem Beratungsgespräch, ein Lehrer in einer Unterrichtssituation, usw.
  10. Angeregt von Wittgenstein brachte ein Teilnehmer auch das Wort Sprachspiel in den Diskurs ein. Eine einzelne isolierte sprachliche Äußerung allein ist oft/ meistens nicht verständlich ohne die Einbettung in die Situation, ohne das Wechselspiel zwischen den Beteiligten, ohne dass alle Beteiligten in der Situation bestimmten (unterstellten) Regeln folgen.
  11. Ferner spielt der zeitliche Ablauf eine Rolle: was war vorher? So erwähnten einige TeilnehmerInnen, dass sie die vorausgehende individuelle Fühlzeit (Meditation) als sehr angenehm, beruhigend, entspannend erlebt hatten und danach ganz anders in den Diskurs eingestiegen sind.

DENKEN ÜBER DAS DENKEN

  1. Dies führte im Verlauf der zweiten Diskursrunde dann zum Versuch, das bislang Gesagte aus einer mehr reflektierenden Position nochmals zu betrachten. Anhand der Frage 1 gab es mehrere Anregungen des Gesprächsleiters, die Erzählperspektive des Teilnehmers mal zu verlassen und über den Diskurs zu reden. Erst als im unteren Teil von Bild 2 Ansätze einer theoretischen Modellbildung skizziert wurden, in der der Sprecher-Hörer als ein abstrakter Kreis erschien, der verschiedene sinnliche Wahrnehmungen hat, verschiedene Motive/ Interessen sowie unterschiedliche Erinnerungen/ erworbene Kompetenzen, setzte sich ansatzweise der Gedanke durch, dass die Ausdruckselemente (gesprochene Laute, geschriebene Zeichen, bestimmte Gesten,…) nicht automatisch, von vornherein, mit etwas anderem, dem, was dann Bedeutung verleiht, assoziiert sind. Man kann etwas sehen (einen Tisch im Zimmer) und etwas hören (einen sprachlichen Ausdruck ‚Tisch‘). Ohne dass man notwendigerweise den gesprochenen Ausdruck ‚Tisch‘ mit einem gesehenen Objekt (Tisch) assoziiert. Allein die Vielzahl der unterschiedlichen Sprachen zeigt, dass der deutsche Ausdruck für Russen, Chinesen, Spanier, Nigerianer, …. nicht zwingend ist. Sie haben das Problem anders gelöst.
  2. Ein Teilnehmer betonte mehrfach, dass man das Sprachgeschehen nicht in seine Bestandteile auflösen könne/ sollte, da man es ansonsten nicht verstehen würde. Mit Hinweis auf das (noch sehr primitive) Modell wurde erläutert, dass das sich Bewusstmachen der unterschiedlichen Komponenten, die in der interne Maschinerie des Sprecher-Hörers (letztlich im Gehirn) solch ein dynamisches Verhalten ermöglichen, kein Gegensatz sein muss zu einem holistischen Blick auf ein dynamisches Sprachgeschehen, eingebettet in Situationsfolgen. Das Zustandekommen von Assoziationen der unterschiedlichsten Arten in komplexen Handlungsfolgen ist gerade der Kern dessen, was man Lernen nennt. Im Lernprozess fließen alle diese unterschiedlichen Komponenten zusammen (aber nicht zwangsweise!).

AUSBLICK MIT FRAGEN

  1. Gegen Ende stellten sich dann viele neue Fragen.
  2. Z.B. die Frage nach den realen, konkreten Objekten in der Sprechsituation und der Frage, ob und wie diese als abstrakte Objekte im Kopf sein können, auch wenn sie in der konkreten Situation nicht mehr vorkommen. (So kann man ja über Gegenstände, Objekte auch in ihrer Abwesenheit sprechen).
  3. Eng damit zusammenhängend die Frage nach allgemeinen Begriffen. Wir reden von Tischen, jeder konkrete Tisch ist aber anders; entsprechend Begriffe wie Stuhl, Tasse, Mensch usw.
  4. Andere Fragestellungen ergaben sich aus dem Eindruck, dass sich die Sprache verrohen würde, vereinfachen.
  5. Oder: welche Bedeutung kommt der Handschrift zu? Kann man auf sie verzichten ohne negative Wirkung auf das Sprachvermögen/ das Sprachverstehen?
  6. Schließlich der Wunsch, dass die einzelnen noch mehr Beispiele aus ihrer persönlichen Sprachlerngeschichte beisteuern, da die Beispiele, die während des Gesprächs spontan erzählt wurden, sehr aufschlussreich waren.

Einen Überblick über alle Einträge zur Philosophiewewrkstatt nach Titeln findet sich HIER.

Einen Überblick über alle Themenbereiche des Blogs finden sich HIER.

Buch: Die andere Superintelligenz. Oder: schaffen wir uns selbst ab? – Kapitel 5 – neu – Version 2

Arbeit, Astrobiologie, Bedeutung, Bedeutung, Bedeutung - biologische, Biologie, Biologische Information, Biologisches Leben, Boltzmann, Chemisches Gleichgewicht, Deacon, Dekodieren, Empfänger, Empfänger, Energie, Energie - freie, Energie Zustandsformen, Entropie, Erde, Erdentstehung, Floridi, Formales System, Fortpflanzen, Freie Energie, Freiheitsgrad (eines Systems), Gedächtnis, Geist, Gleichgewicht, Godfrey-Smith, Information, Information1 - Shannon, Information2 - Bedeutungsrelation, Informationstheorie, Interpretation, Kommunikationskanal, Leben, Leben - Entstehungszeit, Leben - Ursprung und Bedeutung, Leben Definition, Leben Voraussetzungen, Membran, Molekularbiologie, Molekularbiologie, Ontogenese, Phylogenese, Physik, Physik - klassische, Physiker, Population, Prozess, Rauschen, Seele, Selbstorganisation, selbstreferentiell, Selbstreproduktion, Semantik, Semantische Information, Semiotik, Sender, Sender, Shannon, Shannon 1948, Statistische Informationstheorie, Syntax, System, System - adaptiv, Thermodynamik, Thermpodynamik - zweiter Hauptsatz, Verstehen, Zeichen, Zeichenbegriff, Zeichenbenutzer, Zeichenmaterial, Zelle, Zelle - biologische, Zellentstehung

Journal: Philosophie Jetzt – Menschenbild, ISSN 2365-5062, 27.August 2015
URL: cognitiveagent.org
Email: info@cognitiveagent.org

Autor: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

VORBEMERKUNG: Der folgende Text ist ein Vorabdruck zu dem Buch Die andere Superintelligenz. Oder: schaffen wir uns selbst ab?, das im November 2015 erscheinen soll.

Was ist Leben?

Erst die Erde

Etwa 9.2 Mrd Jahre nach dem sogenannten Big Bang kam es zur Entstehung unseres Sonnensystems mit der Sonne als wichtigstem Bezugspunkt. Nur ca. 60 Mio Jahre später gab es unsere Erde. Die Zeitspanne, innerhalb der Spuren von Leben auf der Erde bislang identifiziert wurden, liegt zwischen -4 Mrd Jahre von heute zurück gerechnet bis ca. -3.5 Mrd Jahre. Oder, vom Beginn der Erde aus gesehen, ca. 540 Mio Jahre bis ca. 1 Mrd Jahre nach der Entstehung der Erde.

Alte Bilder vom Leben

Wenn man vom Leben spricht, von etwas Belebtem im Gegensatz zum Unbelebtem, fragt man sich sofort, wie man ‚Leben‘ definieren kann? In der zurückliegenden Geschichte gab es viele Beschreibungs- und Definitionsversuche. Einer, der heute noch begrifflich nachwirkt, ist die Sicht der Philosophie der Antike (ca. -600 bis 650) . Hier wurde das ‚Atmen‘ (gr. ‚pneo‘) als charakteristisches Merkmal für ‚Lebendiges‘ genommen, wodurch es vom ‚Unbelebtem‘ abgegrenzt wurde. Aus dem ‚Atmen‘ wurde zugleich ein allgemeines Lebensprinzip abgeleitet, das ‚Pneuma‘ (im Deutschen leicht missverständlich als ‚Geist‘ übersetzt, im Lateinischen als ’spiritus‘), das sich u.a. im Wind manifestiert und ein allgemeines kosmologisches Lebensprinzip verkörpert, das sowohl die Grundlage für die psychischen Eigenschaften eines Lebewesens bildet wie auch für seine körperliche Lebendigkeit. In der Medizin gab es vielfältige Versuche, das Pneuma im Körper zu identifizieren (z.B. im Blut, in der Leber, im Herzen, im Gehirn und den Nerven). Im philosophischen Bereich konnte das Pneuma ein heißer Äther sein, der die ganze Welt umfasst. Eine andere Auffassung sieht das Pneuma zusammengesetzt aus Feuer und Luft, woraus sich alle Körper der Welt bilden. Das Pneuma wird auch gesehen als die ‚Seele‘, die allein das Leben des Körpers ermöglicht. Bei den Stoikern wird das Pneuma-Konzept zum allumfassenden Begriff einer Weltseele gesteigert. Mit der Zeit vermischte sich der Pneuma-Begriff mit dem Begriff ’nous‘ (Kurzform für ’noos‘)(Englisch als ‚mind‘ übersetzt; Deutsch ebenfalls als ‚Geist‘), um darin die kognitiv-geistige Dimension besser auszudrücken. Weitere einflussreiche begriffliche Koordinierungen finden statt mit dem lateinischen ‚mens‘ (Deutsch auch übersetzt mit ‚Geist‘) und dem hebräischen ‚ruach‘ (im Deutschan ebenfalls mit ‚Geist‘ übersetzt; bekannt in der Formulierung ‚Der Geist Gottes (= ‚ruach elohim‘) schwebte über den Wassern‘; in der Septuaginta, der griechischen Übersetzung der hebräischen Bibel, heißt es ‚pneuma theou‘ (= der Geist Gottes)) (Anmerkung: Diese Bemerkungen sind ein kleiner Extrakt aus der sehr ausführlichen begriffsgeschichtlichen Herleitung in Sandkühler 2010)

Die Zelle im Fokus

War es für die antiken Philosophen, Mediziner und Wissenschaftler noch praktisch unmöglich, die Frage nach den detaillierten Wirkprinzipien des ‚Lebens‘ genauer zu beantworten, erarbeitete sich die moderne Naturwissenschaft immer mehr Einsichten in die Wirkprinzipien biologischer Phänomene (bei Tieren, Pflanzen, Mikroben, molekularbiologischen Sachverhalten), so dass im Laufe des 20.Jahrhunderts klar wurde, dass die Gemeinsamkeit aller Lebensphänomene auf der Erde in jener Superstruktur zu suchen ist, die heute (biologische) Zelle genannt wird.

Alle bekannten Lebensformen auf der Erde, die mehr als eine Zelle umfassen (wir als Exemplare der Gattung homo mit der einzigen Art homo sapiens bestehen aus ca. 10^13 vielen Zellen), gehen zu Beginn ihrer körperlichen Existenz aus genau einer Zelle hervor. Dies bedeutet, dass eine Zelle über alle notwendigen Eigenschaften verfügt, sich zu reproduzieren und das Wachstum eines biologischen Systems zu steuern.

So enthält eine Zelle (Anmerkung: Für das Folgende benutze ich B.Alberts et.al (2008)) alle Informationen, die notwendig sind, um sowohl sich selbst zu organisieren wie auch um sich zu reproduzieren. Die Zelle operiert abseits eines chemischen Gleichgewichts, was nur durch permanente Aufnahme von Energie realisiert werden kann. Obwohl die Zelle durch ihre Aktivitäten die Entropie in ihrer Umgebung ‚erhöht‘, kann sie gegenläufig durch die Aufnahme von Energie auch Entropie verringern. Um einen einheitlichen Prozessraum zu gewährleisten, besitzen Zellen eine Membran, die dafür sorgt, dass nur bestimmte Stoffe in die Zelle hinein- oder herauskommen.

Keine Definition für außerirdisches Leben

Obgleich die Identifizierung der Zelle samt ihrer Funktionsweise eine der größten Errungenschaften der modernen Wissenschaften bei der Erforschung des Phänomens des Lebens darstellt, macht uns die moderne Astrobiologie darauf aufmerksam, dass eine Definition der Lebensphänomene mit Einschränkung des Blicks auf die speziellen Bedingungen auf der Erde nicht unproblematisch ist. Wunderbare Bücher wie „Rare Earth“ von Peter Douglas Ward (Geboren 1949) und Donald Eugene Brownlee (Geboren 1943) „ASTROBIOLOGY. A Multidisciplinary Approach“ von Jonathan I.Lunine (Geb. 1959) machen zumindest sichtbar, wo die Probleme liegen könnten. Lunine diskutiert in Kap.14 seines Buches die Möglichkeit einer allgemeineren Definition von Leben explizit, stellt jedoch fest, dass es aktuell keine solche eindeutige allgemeine Definition von Leben gibt, die über die bekannten erdgebundenen Formen wesentlich hinausgeht. (Vgl. ebd. S.436)

Schrödingers Vision

Wenn man die Charakterisierungen von Leben bei Lunine (2005) in Kap.14 und bei Alberts et.al (2008) in Kap.1 liest, fällt auf, dass die Beschreibung der Grundstrukturen des Lebens trotz aller Abstraktionen tendenziell noch sehr an vielen konkreten Eigenschaften hängen.

Erwin Rudolf Josef Alexander Schrödinger (1887-1961), der 1944 sein einflussreiches Büchlein „What is Life? The Physical Aspect of the Living Cell“ veröffentlichte, kannte all die Feinheiten der modernen Molekularbiologie noch nicht . Schrödinger unterzog das Phänomen des Lebens einer intensiven Befragung aus Sicht der damaligen Physik. Auch ohne all die beeindruckenden Details der neueren Forschung wurde ihm klar, dass das hervorstechendste Merkmal des ‚Biologischen‘, des ‚Lebendigen‘ die Fähigkeit ist, angesichts der physikalisch unausweichlichen Zunahme der Entropie einen gegensätzlichen Trend zu realisieren; statt wachsender Unordnung als Entropie diagnostizierte er eine wachsende Ordnung als negative Entropie, also als etwas, was der Entropie entgegen wirkt.

Diesen Gedanken Schrödingers kann man weiter variieren und in dem Sinne vertiefen, dass der Aufbau einer Ordnung Energie benötigt, mittels der Freiheitsgrade eingeschränkt und Zustände temporär ‚gefestigt‘ werden können.

Fragt sich nur, warum?

Alberts et.al (2008) sehen das Hauptcharakteristikum einer biologischen Zelle darin, dass sie sich fortpflanzen kann, und nicht nur das, sondern dass sie sich selbstmodifizierend fortpflanzen kann. Die Realität biologischer Systeme zeigt zudem, dass es nicht nur um ‚irgendeine‘ Fortpflanzung ging, sondern um eine kontinuierlich optimierende Fortpflanzung.

Metastrukturen

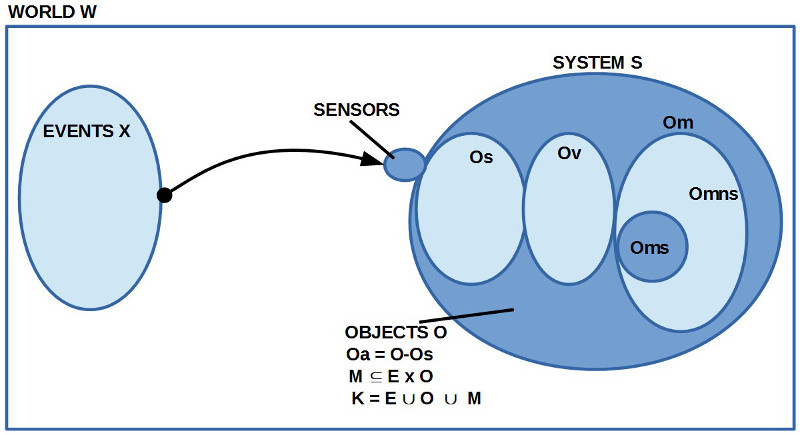
Nimmt man diese Eckwerte ernst, dann liegt es nahe, biologische Zellen als Systeme zu betrachten, die einerseits mit den reagierenden Molekülen mindestens eine Objektebene [O] umfasst und in Gestalt der DNA eine Art Metaebene [M]; zwischen beiden Systemen lässt sich eine geeigneten Abbildung [R] in Gestalt von Übersetzungsprozessen realisieren, so dass die Metaebene M mittels Abbildungsvorschrift R in eine Objektebene O übersetzt werden kann ($latex R: M \longmapsto O$). Damit eine Reproduktion grundsätzlich gelingen kann, muss verlangt werden, dass das System mit seiner Struktur ‚lang genug‘ stabil ist, um solch einen Übersetzungsprozess umsetzen zu können. Wie diese Übersetzungsprozesse im einzelnen vonstatten gehen, ist letztlich unwichtig. Wenn in diesem Modell bestimmte Strukturen erstmals realisiert wurden, dann fungieren sie als eine Art ‚Gedächtnis‘: alle Strukturelemente von M repräsentieren potentielle Objektstrukturen, die jeweils den Ausgangspunkt für die nächste ‚Entwicklungsstufe‘ bilden (sofern sie nicht von der Umwelt ‚aussortiert‘ werden).

Die Rolle dieser Metastrukturen lässt sich letztlich nicht einfach mit den üblichen chemischen Reaktionsketten beschreiben; tut man es dennoch, verliert man die Besonderheit des Phänomens aus dem Blick. Eine begriffliche Strategie, um das Phänomen der ‚wirkenden Metastrukturen‘ in den Griff zu bekommen, war die Einführung des ‚Informationsbegriffs‘.

Information

Grob kann man hier mindestens die folgenden sprachlichen Verwendungsweisen des Begriffs ‚Information‘ im Kontext von Informationstheorie und Molekularbiologie unterscheiden:

  1. Unreflektiert umgangssprachlich (‚Information_0‘)
  2. Anhand des Entscheidungsaufwandes (Bit) (‚Information_1‘)
  3. Rein statistisch (a la Shannon 1948) (‚Information_2‘)
  4. Semiotisch informell (ohne die Semiotik zu zitieren) (‚Semantik_0‘)
  5. Als komplementär zur Statistik (Deacon) (‚Semantik_1‘)
  6. Als erweitertes Shannonmodell (‚Semantik_2‘)

Information_0

Die ‚unreflektiert umgangssprachliche‘ Verwendung des Begriffs ‚Information‘ (hier: ‚Information_0‘) brauchen wir hier nicht weiter zu diskutieren. Sie benutzt den Begriff Information einfach so, ohne weitere Erklärungen, Herleitungen, Begründungen. (Ein Beispiel Küppers (1986:41ff))

Information_1

Die Verwendung des Begriffs Information im Kontext eines Entscheidungsaufwandes (gemessen in ‚Bit‘), hier als ‚Information_1‘ geht auf John Wilder Tukey (1915-2000) zurück.

Information_2

Shannon (1948) übernimmt zunächst diesen Begriff Information_1, verzichtet dann aber im weiteren Verlauf auf diesen Informationsbegriff und führt dann seinen statistischen Informationsbegriff ein (hier: ‚Information_2‘), der am Entropiekonzept von Boltzmann orientiert ist. Er spricht dann zwar immer noch von ‚Information‘, bezieht sich dazu aber auf den Logarithmus der Wahrscheinlichkeit eines Ereignisses, was alles und jedes sein kann. Ein direkter Bezug zu einem ’speziellen‘ Informationsbegriff (wie z.B. Information_1) besteht nicht. Man kann die logarithmierte Wahrscheinlichkeit eines Ereignisses als ‚Information‘ bezeichnen (hier: ‚Information_2‘), aber damit wird der Informationsbegriff inflationär, dann ist alles eine Information, da jedes Ereignis mindestens eine Wahrscheinlichkeit besitzt. (Leider benutzt auch Carl Friedrich von Weizsäcker (1971:347f) diesen inflationären Begriff (plus zusätzlicher philosophischer Komplikationen)). Interessanterweise ist es gerade dieser inflationäre statistische Informationsbegriff Information_2, der eine sehr starke Resonanz gefunden hat.

Semantik 0

Nun gibt es gerade im Bereich der Molekularbiologie zahlreiche Phänomene, die bei einer Beschreibung mittels eines statistischen Informationsbegriffs wichtige Momente ihres Phänomens verlieren. (Dazu eine kleine Übersicht bei Godfrey-Smith, Kim Sterelny (2009)) Ein Hauptkritikpunkt war und ist das angebliche Fehlen von Bedeutungselementen im statistischen Modell von Shannon (1948). Man spricht auch vom Fehlen einer ‚Semantik‘. Allerdings wird eine Diskussion der möglichen Bedeutungsmomente von Kommunikationsereignissen unter Verwendung des Begriffs ‚Semantik‘ auch oft unreflektiert alltagssprachlich vorgenommen (hier: Semantik_0′), d.h. es wird plötzlich von Semantik_0 gesprochen (oft noch erweitert um ‚Pragmatik‘), ohne dass die Herkunft und Verwendung dieses Begriffs in der Wissenschaft der Semiotik weiter berücksichtigt wird. (Ein Beispiel für solch eine verwirrende Verwendungsweise findet sich z.B. wieder bei Weizsäcker (1971:350f), wo Information_0, Information_2 sowie Semantik_0 miteinander frei kombiniert werden, ohne Berücksichtigung der wichtigen Randbedingungen ihrer Verwendung; ganz ähnlich Küppers (1986:61ff); zur Semiotik siehe Noeth (2000)). Ein anderes neueres Beispiel ist Floridi (2015:Kap.3+4) Er benutzt zwar den Begriff ‚Semantik‘ extensiv, aber auch er stellt keinen Bezug zur semiotischen Herkunft her und verwendet den Begriff sehr speziell. Seine Verwendung führt nicht über den formalen Rahmen der statistischen Informationstheorie hinaus.

Semantik 1

Sehr originell ist das Vorgehen von Deacon (2007, 2008, 2010). Er diagnostiziert zwar auch einen Mangel, wenn man die statistische Informationstheorie von Shannon (1948) auf biologische Phänomene anwenden will, statt sich aber auf die schwierige Thematik einer expliziten Semantik einzulassen, versucht er über die Ähnlichkeit des Shannonschen statistischen Informationsbegriffs mit dem von Boltzmann einen Anschluss an die Thermodynamik zu konstruieren. Von dort zum Ungleichgewicht biologischer Systeme, die durch Arbeit und Energieaufnahme ihr Gleichgewicht zu halten versuchen. Diese Interaktionen des Systems mit der Umgebung modifizieren die inneren Zustände des Systems, die wiederum dann das Verhalten des Systems ‚umweltgerecht‘ steuern. Allerdings belässt es Deacon bei diesen allgemeinen Annahmen. Die ‚Abwesenheit‘ der Bedeutung im Modell von Shannon wird über diese frei assoziierten Kontexte – so vermutet man als Leser – mit den postulierten internen Modifikationen des interagierenden Systems begrifflich zusammengeführt. Wie dies genau gedacht werden kann, bleibt offen.

Semantik 2

So anregend die Überlegungen von Deacon auch sind, sie lassen letztlich offen, wie man denn – auch unter Berücksichtigung des Modells von Shannon – ein quasi erweitertes Shannonmodell konstruieren kann, in dem Bedeutung eine Rolle spielt. Hier eine kurze Skizze für solch ein Modell.

Ausgehend von Shannons Modell in 1948 besteht die Welt aus Sendern S, Empfängern D, und Informationskanälen C, über die Sender und Empfänger Signale S eingebettet in ein Rauschen N austauschen können (<S,D,S,N,C> mit C: S —> S x N).

Ein Empfänger-Sender hat die Struktur, dass Signale S in interne Nachrichten M dekodiert werden können mittels R: S x N —> M. Umgekehrt können auch Nachrichten M in Signale kodiert werden mit T: M —> S. Ein minimaler Shannon Sender-Empfänger hat dann die Struktur <M, R, T>. So gesehen funktionieren R und T jeweils als ‚Schnittstellen‘ zwischen dem ‚Äußeren‘ und dem ‚Inneren‘ des Systems.

In diesem minimalen Shannonmodell kommen keine Bedeutungen vor. Man kann allerdings annehmen, dass die Menge M der Nachrichten eine strukturierte Menge ist, deren Elemente Paare der Art (m_i,p_i) in M mit ‚m_i‘ als Nachrichtenelement und ‚p_i‘ als Wahrscheinlichkeit, wie oft dieses Nachrichtenelement im Kanal auftritt. Dann könnte man Shannons Forml H=-Sum(p_i * log2(p_i)) als Teil des Systems auffassen. Das minimale Modell wäre dann <M, R, T, H>.

Will man ‚Bedeutungen‘ in das System einführen, dann muss man nach der Semiotik einen Zeichenbegriff für das System definieren, der es erlaubt, eine Beziehung (Abbildung) zwischen einem ‚Zeichenmaterial‚ und einem ‚Bedeutungsmaterial‚ zu konstruieren. Nimmt man die Signale S von Shannon als Kandidaten für ein Zeichenmaterial, fragt sich, wie man das Bedeutungsmaterial B ins Spiel bringt.

Klar ist nur, dass ein Zeichenmaterial erst dann zu einem ‚Zeichen‘ wird, wenn der Zeichenbenutzer in der Lage ist, dem Zeichenmaterial eine Bedeutung B zuzuordnen. Eine einfache Annahme wäre, zu sagen, die dekodierten Nachrichten M bilden das erkannte Zeichenmaterial und der Empfänger kann dieses Material irgendwelchen Bedeutungen B zuordnen, indem er das Zeichenmaterial M ‚interpretiert‚, also I : M —> B. Damit würde sich die Struktur erweitern zu <B, M, R, T, H, I>. Damit nicht nur ein Empfänger ‚verstehen‘ kann, sondern auch ‚mitteilen‘, müsste der Empfänger als Sender Bedeutungen auch wieder ‚umgekehrt lesen‘ können, also -I: B —> M. Diese Nachrichten könnten dann wieder mittels T in Signale übersetzt werden, der Kanal sendet diese Signale S angereichert mit Rauschen N zum Empfänger, usw. Wir erhalten also ein minimal erweitertes Shannon Modell mit Bedeutung als <B, M, R, T, H, I, -I>. Ein Sender-Empfänger kann also weiterhin die Wahrscheinlichkeitsstruktur seiner Nachrichten auswerten; zusätzlich aber auch mögliche Bedeutungsanteile.

Bliebe als Restfrage, wie die Bedeutungen B in das System hineinkommen bzw. wie die Interpretationsfunktion I entsteht?

An dieser Stelle kann man die Spekulationen von Deacon aufgreifen und als Arbeitshypothese annehmen, dass sich die Bedeutungen B samt der Interpretationsbeziehung I (und -I) in einem Adaptionsprozess (Lernprozess) in Interaktion mit der Umgebung entwickeln. Dies soll an anderer Stelle beschrieben werden.

Für eine komplette Beschreibung biologischer Phänomene benötigt man aber noch weitere Annahmen zur Ontogense und zur Phylogense. Diese seien hier noch kurz skizziert. (Eine ausführliche formale Darstellung wird anderswo nachgeliefert).

Ontogenese

Von der Lernfähigkeit eines biologischen Systems muss man die Ontogenese unterscheiden, jenen Prozess, der von der Keimzelle bis zum ausgewachsenen System führt.

Die Umsetzung der Ontogenese in einem formalen Modell besteht darin, einen Konstruktionsprozess zu definieren, das aus einem Anfangselement Zmin das endgültige System Sys in SYS erstellen würde. Das Anfangselement wäre ein minimales Element Zmin analog einer befruchteten Zelle, das alle Informationen enthalten würde, die notwendig wären, um diese Konstruktion durchführen zu können, also Ontogenese: Zmin x X —> SYS. Das ‚X‘ stünde für alle die Elemente, die im Rahmen einer Ontogenese aus der Umgebung ENV übernommen werden müssten, um das endgültige system SYS = <B, M, R, T, H, I, -I> zu konstruieren.

Phylogenese

Für die Reproduktion der Systeme im Laufe der Zeiten benötigte man eine Population von Systemen SYS, von denen jedes System Sys in SYS mindestens ein minimales Anfangselement Zmin besitzt, das für eine Ontogenese zur Verfügung gestellt werden kann. Bevor die Ontogenese beginnen würde, würden zwei minimale Anfangselemente Zmin1 und Zmin2 im Bereich ihrer Bauanleitungen ‚gemischt‘. Man müsste also annehmen, dass das minimale System um das Element Zmin erweitert würde SYS = <B, M, Zmin, R, T, H, I, -I>.

Erstes Zwischenergebnis

Auffällig ist also, dass das Phänomen des Lebens

  1. trotz Entropie über dynamische Ungleichgewichte immer komplexere Strukturen aufbauen kann.
  2. innerhalb seiner Strukturen immer komplexere Informations- und Bedeutungsstrukturen aufbaut und nutzt.

So wie man bislang z.B. die ‚Gravitation‘ anhand ihrer Wirkungen erfasst und bis heute erfolglos zu erklären versucht, so erfassen wir als Lebende das Leben anhand seiner Wirkungen und versuchen bis heute auch erfolglos, zu verstehen, was hier eigentlich passiert. Kein einziges physikalisches Gesetzt bietet auch nur den leisesten Anhaltspunkt für dieses atemberaubende Geschehen.

In dieser Situation den Menschen als eine ‚vermutlich aussterbende Art‘ zu bezeichnen ist dann nicht einfach nur ‚gedankenlos‘, sondern im höchsten Maße unwissenschaftlich, da es letztlich einer Denkverweigerung nahe kommt. Eine Wissenschaft, die sich weigert, über die Phänomene der Natur nachzudenken, ist keine Wissenschaft.

Fortsetzung Folgt.

QUELLEN

  1. H.J. Sandkühler (Hg.), 2010, „Enzyklopädie Philosophie“, Hamburg: Felix Meiner Verlag, Band 1: Von A bis H, Kapitel: Geist, SS.792ff
  2. B.Alberts et.al (Hg.), 2008, „Molecular Biology of the CELL“, Kap.1, 5.Aufl., New York: Garland Science, Taylor & Francis Group
  3. Peter Douglas Ward und `Donald Eugene Brownlee (2000),“Rare Earth: Why Complex Life Is Uncommon in the Universe“, New York: Copernikus/ Springer,
  4. Jonathan I.Lunine (2005), „ASTROBIOLOGY. A Multidisciplinary Approach“, San Francisco – Boston – New York et al.: Pearson-Addison Wesley
  5. Zu Schroedinger 1944: Based on Lectures delivered under the auspices of the Institute at Trinity College, Dublin, in February 1943, Cambridge: University Press. 1944. Ich selbst habe die Canto Taschenbuchausgabe der Cambridge University von 1992 benutzt. Diese Ausgabe enthält ‚What is Life?‘, ‚Mind from Matter‘, sowie autobiographischen Angaben und ein Vorwort von Roger Penrose
  6. Anmerkung zu Schroedinger 1944: Sowohl James D. Watson (2003) wie auch ähnlich Francis Crick (1990) berichten, dass Schrödingers Schrift (bzw. einer seiner Vorträge) sie für ihre Erforschung der DNA stark angeregt hatte.
  7. James D.Watson und A.Berry(2003), „DNA, the Secret of Life“, New York: Random House
  8. Francis Crick (1990),„What Mad Pursuit: A Personal View of Scientific Discovery“, Reprint, Basic Books
  9. Peter Godfrey-Smith und Kim Sterelny (2009) Biological Information“, in: Stanford Enyclopedia of Philosophy
  10. Carl Friedrich von Weizsäcker (1971), „Die Einheit der Natur“, München: Carl Hanser Verlag
  11. Bernd-Olaf Küppers (1986), „Der Ursprung biologischer Information. Zur Naturphilosophie der Lebensentstehung“, München – Zürich: Piper Verlag.
  12. Claude E. Shannon, A mathematical theory of communication. Bell System Tech. J., 27:379-423, 623-656, July, Oct. 1948
  13. Claude E. Shannon; Warren Weaver (1949) „The mathematical theory of communication“. Urbana – Chicgo: University of Illinois Press.
  14. Noeth, W., Handbuch der Semiotik, 2. vollst. neu bearb. und erw. Aufl. mit 89 Abb. Stuttgart/Weimar: J.B. Metzler, xii + 668pp, 2000
  15. Luciano Floridi (2015) Semantic Conceptions of Information, in: Stanford Enyclopedia of Philosophy
  16. Deacon, T. (2007), Shannon-Boltzmann-Darwin: Redfining information. Part 1. in: Cognitive Semiotics, 1: 123-148
  17. Deacon, T. (2008), Shannon-Boltzmann-Darwin: Redfining information. Part 2. in: Cognitive Semiotics, 2: 167-194
  18. Terrence W.Deacon (2010), „What is missing from theories of information“, in: INFORMATION AND THE NATURE OF REALITY. From Physics to Metaphysics“, ed. By Paul Davies & Niels Henrik Gregersen, Cambridge (UK) et al: Cambridge University Press, pp.146 – 169

Einen Überblick über alle Blogbeiträge des Autors cagent nach Titeln findet sich HIER.

BUCHPROJEKT 2015 – Zwischenreflexion 18.August 2015 – INFORMATION IN DER MOLEKULARBIOLOGIE – Maynard-Smith

Chromosom, DNA als Gedächtnis, DNA-Molekül, Gedächtnis, Genetik, Genom, Information, Information1 - Shannon, Information2 - Bedeutungsrelation, Informationsstrukturen, Informationstheorie, Informationsverarbeitung, Informationsverarbeitung biologische, John Maynard Smith, Moleküle, RNA - Boten (mRNA), RNA - Ribosomal, RNA - Transfer (tRNA), RNA-Molekül, Schroedinger, Semantik, Semiotik, Semiotische Maschine, Semiotisches System, Shannon, Transkription, Translation, Weaver, Zeichen, Zeichen, Zeichenbegriff, Zeichenbenutzer, Zeichenmaterial, Zelle, Zelle - biologische, Zellentstehung

Der folgende Beitrag bezieht sich auf das Buchprojekt 2015.

SPANNENDER PUNKT BEIM SCHREIBEN

1. Das Schreiben des Buches hat zu einem spannenden Punkt geführt, der mich seit Jahren umtreibt, den ich aber nie so richtig zu packen bekommen habe: alle große begriffliche Koordinaten laufen im Ereignis der Zelle als einer zentralen Manifestation von grundlegenden Prinzipien zusammen. Die Physik hat zwar generelle Vorarbeiten von unschätzbarem Wert geleistet, aber erst das Auftreten von selbst reproduzierenden molekularen Strukturen, die wir (biologische) Zellen nennen, macht Dynamiken sichtbar, die ‚oberhalb‘ ihrer ‚Bestandteile‘ liegen. Dies könnte man analog dem physikalischen Begriff der ‚Gravitation‘ sehen: dem physikalischen Begriff entspricht kein direktes Objekt, aber es beschreibt eine Dynamik, eine Gesetzmäßigkeit, die man anhand des Verhaltens der beobachtbaren Materie indirekt ‚ableitet‘.

DYNAMIK BIOLOGISCHER ZELLEN

2. Ähnlich verhält es sich mit verschiedenen Dynamiken von biologischen Zellen. Die Beschreibung ihrer einzelnen Bestandteile (Chromatin, Mitochondrien, Golgiapparat, Membran, …) als solcher sagt nichts darüber aus, was tatsächlich eine biologische Zelle charakterisiert. Ihre Haupteigenschaft ist die generelle Fähigkeit, eingebettet in eine allgemeine Entropiezunahme sich eine Struktur zu generieren, die sich temporär funktionsfähig halten kann und in der Lage ist, Informationen zu sammeln, mittels deren sie sich selbst so kopieren kann, dass die Kopie sich von neuem zu einer funktionsfähigen Struktur aufbauen kann. Wie dies im einzelnen chemisch realisiert wurde, ist beeindruckend, es ist atemberaubend, aber es ist letztlich austauschbar; für die Gesamtfunktion spielen die chemischen Details keine Rolle.

BEGRIFF INFORMATION

3. Und hier beginnt das Problem. Obwohl es von einem theoretischen Standpunkt aus klar ist, dass die Details noch nicht die eigentliche Geschichte erzählen, wird in den vielen umfangreichen Büchern über Genetik und Molekularbiologie die eigentliche ‚Story‘ nicht erzählt. Dies fängt schon an mit dem wichtigen Begriff der Information. Spätestens seit Schrödingers Buch von 1944 „What is Life?“ ist klar, dass das selbstreproduktive Verhalten von Zellen ohne das Genom nicht funktioniert. Und es wurde auch sehr bald der Begriff der Information eingeführt, um den ‚Inhalt‘ des Genoms theoretisch zu klassifizieren. Das Genom enthält ‚Informationen‘, aufgrund deren in einer Vererbung neue hinreichend ähnlich Strukturen entstehen können.

STATISTISCHER INFORMATIONSBEGRIFF

4. Leider wurde und wird der Informationsbegriff im Sinne des rein statistischen Informationsbegriffs von Shannon/ Weaver (1948) benutzt, der explizit Fragen möglicher Bedeutungsbezüge (Semantik) außen vor lässt. Damit ist er eigentlich weitgehend ungeeignet, der Rolle der im Genom verfügbaren Informationen gerect zu werden.

MEHR ALS STATISTIK

5. Einer, der diese Unzulänglichkeit des rein statistischen Informationsbegriffs für die Beschreibung der Rolle der Information im Kontext des Genoms und der Zelle samt ihrer Reproduktionsdynamik immer kritisiert hatte, war John Maynard Smith (1920 – 2004). In seinem Artikel “ The concept of information in biology“ von 2000 kann man dies wunderbar nachlesen.

6. Zwar hat auch Maynard Smith keine explizite übergreifende Theorie der Reproduktionsdynamik, aber er kann an verschiedenen Eigenschaften aufweisen, dass der rein statistische Informationsbegriff nicht ausreicht.

7. Während im Shannon-Weaver Modell ein fester Kode A von einem Sender in Transportereignisse übersetzt (kodiert) wird, die wiederum in den festen Kode A von einem Empfänger zurückübersetzt (dekodiert) werden, ist die Lage bei der Zelle anders.

8. Nimmt man an, dass der zu sendende Kode das DNA-Molekül ist, das in seiner Struktur eine potentielle Informationssequenz repräsentiert, dann ist der Sender eine Zelle in einer Umgebung. Der ‚DNA-Kode‘ (der feste Kode A) wird dann umgeschrieben (Transskription, Translation) in zwei verschiedene Kodes (mRNA, tRNA). Während man die Zustandsform des mRNA-Moleküls noch in Korrespondenz zum DNA-Kode sehen kann (abr nicht vollständig), enthalten die verschiedenen tRNA-Moleküle Bestandteile, die über den ursprünglichen DNA-Kode hinausgehen. Daraus wird dann eine Proteinstruktur erzeugt, die sowohl eine gewisse Kopie des ursprünglichen DNA-Moleküls (Kode A) enthält, aber auch zusätzlich einen kompletten Zellkörper, der mit dem Kode A nichts mehr zu tun hat. Außerdem gibt es den Empfänger bei Beginn der Übermittlung noch gar nicht. Der Empfänger wird im Prozess der Übermittlung erst erzeugt! Anders formuliert: beim biologischen Informationsaustausch im Rahmen einer Selbstreproduktion wird zunächst der potentielle Empfänger (eine andere Zelle) erzeugt, um dann den DNA-Kode im Empfänger neu zu verankern.

9. Innerhalb dieses Gesamtgeschehens gibt es mehrere Bereiche/ Phasen, in denen das Konzept eines rein statistischen Informationsbegriffs verlassen wird.

10. So weist Maynard Smith darauf hin, dass die Zuordnung von DNA-Sequenzen zu den später erzeugten Proteinen mindestens zweifach den statistischen Informationsbegriff übersteigt: (i) die erzeugten Proteinstrukturen als solche bilden keine einfache ‚Übersetzung‘ das DNA-Kodes verstanden als eine syntaktische Sequenz von definierten Einheiten eines definierten endlichen Alphabets. Die Proteinmoleküle kann man zwar auch als Sequenzen von Einheiten eines endlichen Alphabets auffassen, aber es handelt sich um ein ganz anderes Alphabet. Es ist eben nicht nur eine reine ‚Umschreibung‘ (‚Transkription‘), sondern eine ‚Übersetzung‘ (‚Translation‘, ‚Translatio‘), in die mehr Informationen eingehen, als die Ausgangssequenzen im DNA-Kode beinhalten. (ii) Der DNA-Kode enthält mindestens zwei Arten von Informationselementen: solche, die dann in Proteinstrukturen übersetzt werden können (mit Zusatzinformationen), und solche, die die Übersetzung der DNA-Informationselemente zeitlich steuern. Damit enthält der DNA-Kode selbst Elemente, die nicht rein statistisch zu betrachten sind, sondern die eine ‚Bedeutung‘ besitzen, eine ‚Semantik‘. Diese Bedeutung st nicht fixiert; sie kann sich ändern.

ALLGEMEINE ZEICHENLEHRE = SEMIOTIK

11. Für Elemente eines Kodes, denen ‚Bedeutungen‘ zugeordnet sind, gibt es in der Wissenschaft das begriffliche Instrumentarium der allgemeinen Zeichenlehre, spricht ‚Semiotik‘ (siehe z.B. Noeth 2000).

12. Nimmt man die empirischen Funde und die semiotische Begrifflichkeit ernst, dann haben wir es im Fall der Zelle also mit eindeutigen (und recht komplexen) Zeichenprozessen zu; man könnte von der Zelle in diesem Sinne also von einem ’semiotischen System‘ sprechen. Maynard Smith deutet den Grundbegriff von Jacques Lucien Monod (1910-1976) ‚gratuity‘ im Sinne, dass Signale in der Biologie ‚Zeichen‘ seien. Ob dies die Grundintention von Monod trifft, ist eine offene Frage; zumindest lässt die Maschinerie, die Monod beschreibt, diese Deutung zu.

13. Eine zusätzliche Komplikation beim biologischen Zeichenbegriff ergibt sich dadurch, dass eine Zelle ja nicht ‚isoliert‘ operiert. Eine Zelle ist normalerweise Teil einer Population in einer bestimmten Umgebung. Welche Strukturen der Proteinaufbauprozess (Wachstum, Ontogenese) auch hervorbringen mag, ob er gewisse Zeiten überdauert (gemessen in Generationen), hängt entscheidend davon ab, ob die Proteinstruktur in der Interaktion mit der Umgebung ‚hinreichend lange‘ jene ‚Arbeit‘ verrichten kann, die notwendig ist, um eine Selbstreproduktion zu ermöglichen.

14. Ob eine Proteinstruktur in diesem weiterführenden Sinne ‚lebensfähig‘ ist, hängt also entscheidend davon ab, ob sie zur jeweiligen Umgebung ‚passt‘. Eine lebensfähige Proteinstruktur ist in diesem Sinne – von einer höheren theoretischen Betrachtungsweise aus gesehen – nichts anderes als ein auf Interaktion basierendes ‚Echo‘ zur vorgegebenen Umgebung.

15. Dass dies ‚Echo‘ nicht ’stagniert‘, nicht ‚auf der Stelle tritt‘, nicht ‚um sich selbst kreist‘, liegt entscheidend daran, dass die ‚letzte‘ Struktur den Ausgangspunkt für ‚weitere Veränderungen‘ darstellt. Die Zufallsanteile im gesamten Selbstreproduktionsprozess fangen also nicht immer wieder ‚von vorne‘ an (also keine ‚Auswahl mit Zurücklegen‘), sondern sie entwickeln eine Informationsstruktur ‚weiter‘. In diesem Sinne bildet die Informationssequenz des DNA-Moleküls auch einen ‚Speicher‘, ein ‚Gedächtnis‘ von vergangenen erfolgreichen Versuchen. Je mehr Zellen in einer Population verfügbar sind, umso größer ist diese molekulare Erfolgsgedächtnis.

Diese Fortsetzung war nicht die letzte Zwischenreflexion. Es geht noch weiter: HIER

QUELLEN

Schroedinger, E. „What is Life?“ zusammen mit „Mind and Matter“ und „Autobiographical Sketches“. Cambridge: Cambridge University Press, 1992 (‚What is Life‘ zuerst veröffentlicht 1944; ‚Mind an Matter‘ zuerst 1958)
Claude E. Shannon, „A mathematical theory of communication“. Bell System Tech. J., 27:379-423, 623-656, July, Oct. 1948 (URL: http://cm.bell-labs.com/cm/ms/what/shannonday/paper.html; last visited May-15, 2008)
Claude E. Shannon; Warren Weaver (1948) „The mathematical theory of communication“. Urbana – Chicgo: University of Illinois Press.
John Maynard Smith (2000), „The concept of information in biology“, in: Philosophy of Science 67 (2):177-194
Noeth, W., Handbuch der Semiotik, 2. vollst. neu bearb. und erw. Aufl. mit 89 Abb. Stuttgart/Weimar: J.B. Metzler, xii + 668pp, 2000
Monod, Jacques (1971). Chance and Necessity. New York: Alfred A. Knopf

Einen Überblick über alle Blogbeiträge des Autors cagent nach Titeln findet sich HIER.

Buch: Die andere Superintelligenz. Oder: schaffen wir uns selbst ab? – Kapitel 5

Abstraktion, akustisch, Allgemeinbegriff, Alltagssprache, Außenwelt, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - empirisch, Bedeutung - kontingent, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Bedeutungsraum, Bewußtsein, Bewusstsein als Erkenntnisraum, exprimentelle, Gegenstand - intentionaler, Gegenstand natürlich, Gegenstand technisch, Interpretation, Kategorien, Klasse, Kommunikation, Morris, Objekt, Objekt erkanntes, Peirce, Phänomenologische Zeichentheorie, Prozess, Psychologie, Raum, Raumstruktur, Saussure, Semantik, Semiotik, Semiotisches System, Sensorische Daten, Situation, Sprache, Sprache und Denken, Sprachliche Äußerung, Sprachmaterial, Sprachpsychologie, Sprachspiel, Sprecher, Stimulation, Stimulus, Verhalten, verhaltensbasierte, Verhaltensbasierte Psychologie, Verhaltensfunktion, Verhaltensfunktion - empirische, Verhaltensorientiert, Verhaltensregel, visuell, Wahrnehmen, Wahrnehmung, Wahrnehmungsobjekt, Zeichen, Zeichen, Zeichenbegriff, Zeichenbenutzer, Zeichenbenutzung

VORBEMERKUNG: Der folgende Text ist ein Vorabdruck zu dem Buch Die andere Superintelligenz. Oder: schaffen wir uns selbst ab?, das im November 2015 erscheinen soll

Das Wunder des Zeichens

Wenn wir zu verstehen beginnen, dass die wunderbare Welt unseres Erkennens im Gehirn stattfindet, das in unserem Körper eingeschlossen getrennt von der Welt existiert, kann sich die Frage stellen, wie denn das Gehirn von Dir und mein Gehirn miteinander kommunizieren können. Wie erfahre ich, was Du willst, und Du, was ich will? Woher kann ich wissen, warum Du diese Handlung gut findest, und wie erfährst Du, warum ich die andere Handlung gut finde?

Diese Fragen zielen auf das Wunder der Koordination zwischen Menschen, aber letztlich auch zwischen Tieren, auch zwischen Pflanzen, ja generell: wieso können biologische Zellen ihr Verhalten koordinieren?

Hier gibt es noch viele Fragen, auf die die Wissenschaften bis heute keine voll befriedigenden Antworten gefunden hat. Auf einige dieser Fragen werde ich weiter unten noch eingehen. Jetzt, hier, in diesem Kapitel, soll es um die Frage gehen, wie wir Menschen die Frage der Kommunikation mittels Sprache — zumindest ansatzweise — gelöst haben.

Auf etwas zeigen

Wenn Menschen mit anderen zusammen am Tisch sitzen und Essen ist es oft so, dass man einen Gegenstand vom Tisch benötigt, der weiter weg steht und man denjenigen bittet, der am nächsten dran sitzt, einem den Gegenstand zu reichen.

Man kann dies tun, indem man mit der Hand, den Fingern, mit dem Gesicht in die Richtung des Gegenstandes deutet und die andere Person ‚erkennt‘ aus der Richtung und dem, was sich auf dem Tisch befindet, was ‚gemeint‘ ist; die andere Person deutet dann vielleicht selbst auf diesen Gegenstand, mit einem fragenden Blick, und wenn es der Gegenstand ist, den man meint, dann nickt man vielleicht, freundlich, mit einem Lächeln, und die andere Person reicht einem den Gegenstand.

In diesem Fall waren es Bewegungen des Körpers und bestimmte Körperhaltungen die in einer konkreten Situation mit Teilen der Situation in Interaktion treten und die, eine andere ‚kooperierenden Person‘ vorausgesetzt, von dieser anderen kooperierenden Person mit bestimmten Teilen der Situation ‚in Beziehung gesetzt‘ werden. Eine Handbewegung ist in diesem Fall nicht einfach eine Handbewegung ‚für sich‘, sondern eine Handbewegung als Teil einer größeren Situation, wo der ‚Andere‘ die Handbewegung mit einem bestimmten Teil der Situation, einem Gegenstand G, in eine ‚Beziehung‘ bringt. Diese Beziehung ist selbst kein realer Gegenstand sondern ist eine der vielen ‚möglichen gedachten Beziehungen‘ im Kopf des Anderen zwischen der beobachteten Handbewegung und den verschiedenen Gegenständen auf dem Tisch. Durch den fragenden Blick will der Andere wissen, ob seine ‚gedachte Beziehung‘ jene Beziehung ist, die der Bittende ‚intendiert‘ (sich vorgestellt, gedacht, …) hatte. Wenn der Bittende bestätigend nickt, dann fühlt der Andere sich ‚bestätigt‘ und nimmt die hypothetische gedachte Beziehung als jene Beziehung, die jetzt in dieser Situation vom Bittenden ‚gemeint‘ ist. Punktuell, kurzfristig wurde also im Raum der vielen Möglichkeiten eine bestimmte mögliche Beziehung als hier und jetzt gewollte gedacht und durch Bewegungen ‚manifestiert‘ (ausgedrückt, mitgeteilt, …).

Wenn wir dieses alltägliche Beispiel verallgemeinern, dann haben wir folgende (theoretische) Zutaten:

  1. Wir haben mindestens zwei Teilnehmer A und B, die ein Kommunikationsspiel spielen.
  2. Wir unterstellen bei jedem Teilnehmer ein Bewusstsein, das einem Teilnehmer ermöglicht, Eigenschaften der Außenwelt W in seinem Bewusstsein ‚hinreichend gut‘ zu ‚repräsentieren‘.
  3. Jeder Teilnehmer hat einen Körper, der von dem anderen wahrgenommen werden kann und der Eigenschaften besitzt, die eine Unterscheidung von Körperhaltungen und Körperbewegungen erlauben.
  4. In der gemeinsam geteilten Situation (als Teil der Außenwelt) gibt es Objekte, die Eigenschaften besitzen, wodurch sie sich voneinander unterscheiden und aufgrund deren sie von den Teilnehmern ‚wahrgenommen‘ werden können.
  5. Wir unterscheiden zwischen der ‚Stimulation‘ der Sinnesorgane in Gestalt von sensorischem Input I durch die Objekte OBJ der Außenwelt (als $latex stim: SIT \times OBJ \longmapsto I$) und der eigentlichen Wahrnehmung als Ergebnis der internen Verarbeitung der Stimulation I in bewusste Perzepte P (als $latex perc: I \times IS \longmapsto IS \times P$) (‚IS‘ steht für irgendwelche internen Zustände, die bei diesem Prozess auch noch eine Rolle spielen.). Dies berücksichtigt, dass die gleichen Außenweltreize von verschiedenen Anderen unterschiedlich verarbeitet werden können.
  6. Objekte in der Außenwelt werden — auf unterschiedliche Weise — so wahrgenommen, als ob sie sich in einem dreidimensionalen Raum befinden. Dies bedeutet, eine Situation hat eine ‚Raumstruktur‘, in der die Objekte in bestimmten Positionen und Lagen vorkommen. Dadurch ergeben sich zwischen den Objekten charakteristische räumliche Beziehungen. Während die Stimulation der Sinnesorgane diese räumlichen Strukturen partiell ‚vereinfacht‘, kann die Wahrnehmung mit Unterstützung des Gehirns daraus partiell räumliche Strukturen ‚zurückrechnen‘.
  7. Wenn zwei Gegenstände sich im Raum der Außenwelt so befinden, dass wir sie wahrnehmen können (z.B. eine Schüssel auf dem Tisch und eine Hand, die in diese ‚Richtung‘ deutet), können wir außer der räumlichen Beziehung auch andere mögliche Beziehungen (z.B. eine ‚Zeigebeziehung‘) wahrnehmen. Diese Beziehungen existieren als mögliche ‚gedachte Beziehungen‘ im Bewusstsein eines Teilnehmers. Ein Teilnehmer kann sich unendlich viele Beziehungen denken.
  8. Dass ein Anderer A zwei Objekte der Außenwelt mit einer ‚gedachten Beziehung‘ verbinden kann, die der Bittende B in seinem Bewusstsein ’sich vorstellt’/ ‚denkt‘, setzt ferner voraus, dass es zwischen der Wahrnehmung und dem ‚Vorstellen’/ ‚Denken‘ zwischen A und B hinreichend viel ‚Ähnlichkeit‘ gibt. Könnte ein A grundsätzlich sich nicht jene ‚Beziehungen‘ ‚vorstellen‘, die sich B vorstellt, wenn er mit seiner Hand in Richtung eines bestimmten Gegenstands (z.B. der einen roten Schüssel …) deutet, dann könnte B so viel deuten wie er will, der Andere A würde sich einfach nicht vorstellen

Nach dieser — noch immer vereinfachenden — Darstellung des Sachverhalts, können wir uns dem Begriff des Zeichens zuwenden.

Der Begriff des Zeichens

Mit dieser Frage gerät man in den Bereich der allgemeinen Wissenschaft von den Zeichen, der Semiotik (Anmerkung: Die Geschichte der Semiotik ist lang und vielschichtig. Einen guten Überblick bietet Winfried Noeth in seinem ‚Handbuch der Semiotik‘ von 2000, publiziert von J.B. Metzler (Stuttgart/Weimar)). Obwohl es je nach Zeit und Denkmode sehr unterschiedliche Formulierungen gibt, kann man eine Kernstruktur erkennen, die sich in allen unterschiedlichen Positionen durchhält.

Allerdings sollte man sich vorab klar machen, ob man — wie es historisch zunächst der Fall war — den Begriff des Zeichens primär durch Bezugnahme auf den Raum des Bewusstseins charakterisieren will, oder durch Bezugnahme auf das beobachtbare Verhalten (wie es die empirischen Wissenschaften favorisieren).

Der berühmteste Vertreter einer bewusstseinszentrierten Vorgehensweise ist Charles Sanders Peirce (1839 – 1914). Für den verhaltensorientierten Ansatz einflussreich war Charles William Morris (1901 – 1979). Eine Kombination aus bewusstseinsbasierten und verhaltensorientierten Aspekten bietet Ferdinand de Saussure (1857 – 1913).

Der Gebrauch eines Zeichens setzt — wie zuvor — eine Kommunikationssituation voraus mit mindestens zwei Teilnehmern, die mit ihren Körpern in der Situation anwesend sind und über hinreichend gleiche Körperstrukturen für Wahrnehmung und Denken verfügen.

Am Beispiel der Situation des Essens möchte ich die rote Schüssel mit dem Nachtisch gereicht bekommen; diese steht nicht in meiner Griffweite. Ich sehe meine Schwester Martina so sitzen, dass Sie mir die Schüssel reichen könnte. Ohne Sprache könnte ich nur mit Handbewegungen und Gesichtsausdrücken versuchen, ihr klar zu machen, was ich möchte. Mit Sprache könnte ich Laute erzeugen, die als Schallwellen ihr Ohr erreichen und sagen würden ‚Hallo M, kannst Du mir bitte mal die rote Schüssel reichen?‘. Sofern meine Schwester Deutsch kann (was der Fall ist), wird sie diese Schallwellen in ihrem Kopf so ‚übersetzen‘, dass sie einen Bezug herstellt zu ihrer Wahrnehmung der roten Schüssel, zur Wahrnehmung von mir, und wird eine Aktion einleiten, mir die Schüssel zu reichen.

Der gesprochene Satz ‚Hallo M, kannst Du mir bitte mal die rote Schüssel reichen?‘ als ganzer stellt ein Ausdrucksmittel dar, bildet ein Material, mittels dessen ein Sprecher (in dem Fall ich), einen Hörer (in dem Fall meine Schwester) in die Lage versetzt, nur aufgrund des Schalls einen Bezug zu einem realen Objekt herzustellen und dieses Objekt in eine Handlung (mir das Objekt rüber reichen) einzubetten. Meine Schwester als Hörerin ist damit interpretierend tätig; sie stellt aktiv eine Verbindung her zwischen dem gehörten Schall und Elementen ihrer Wahrnehmung der Situation. Diese Interpretation befähigt sie, eine Handlung zu planen und auszuführen.

Rein verhaltensorientiert kann man sagen, dass die gesamte sprachliche Äußerung ein Zeichenmaterial darstellt, das vom Hörer intern ‚verarbeitet‘ wird, was zu einer bestimmten Handlung führt (die rote Schüssel reichen). Der Hörer nimmt hier eine Interpretation (Int) vor, durch die der Schall, das Zeichenmaterial (ZM) in Beziehung gesetzt wird zu etwas Wahrgenommenem; dies führt wiederum zu einer beobachtbaren Handlung, die damit zur Bedeutung (M) des Zeichenmaterials wird: $latex Int: ZM \longmapsto M$. Anders ausgedrückt, das Gesagte, der Sprachschall, bekommt durch diesen Zusammenhang eine neue Funktion; der Schall steht nicht mehr nur ‚für sich alleine‘, sondern es spielt eine Rolle in einer Beziehung. Damit wird das an sich neutrale Schallereignis zu einem ‚Zeichen‘. Ein Hörer verwandelt mit seiner Interpretation ein an sich neutrales Ereignis in ein Zeichen für etwas anderes, was man die Bedeutung des Zeichens nennt.

Als Wissenschaftler kann man hier weiter verallgemeinern und den Hörer als ein Input-Output-System betrachten mit dem Sprachschall und den visuellen Wahrnehmungen als Input I und dem beobachtbaren Verhalten als Output O und der Interpretation Int als Verhaltensfunktion $latex \phi$, geschrieben $latex \phi: I \times IS \longmapsto IS \times O$

Interpretieren

Wer die Thematik ‚Zeichen‘, ‚Semiotik‘, ‚Sprache‘, Sprachverstehen‘ usw. ein wenig kennt, der weiß, dass wir uns damit einer Materie genähert haben, die sehr umfangreich und beliebig kompliziert ist, so kompliziert, dass fast alle wirklich interessanten Fragen noch kaum als gelöst bezeichnet werden können. Ich beschränke mich daher hier nur auf einige Kernpunkte. Nach Bedarf müssten wir das vertiefen.

Wie man an dieser Stelle ahnen kann, ist der Vorgang des Interpretierens das eigentliche Herzstück des Zeichenbegriffs. Hier geschieht die Zuordnung zwischen gehörtem Schall (oder gelesenem Text, oder gesehenen Gesten, oder …) zu anderen bekannten Wissensinhalten, vorzugsweise zu Wahrnehmungselementen der aktuellen Situation. Will man die Details dieses Interpretationsprozesses beschreiben, hat man mit einem verhaltensbasierten Ansatz ein Problem: alles, was sich im ‚Innern‘ eines biologischen Systems abspielt, ist zunächst nicht beobachtbar. Da hilft es auch nicht, wenn man heute einen Körper ‚aufmachen‘ kann und Körperorgane, Zellen, Prozesse in den Zellen untersuchen kann. Schaltzustände von Zellen, speziell Gehirnzellen, sagen als solche nichts über das Verhalten. Es sei denn, man ist in der Lage, explizit einen Zusammenhang zwischen den Zuständen von Gehirnzellen und beobachtbarem Verhalten herzustellen, was in der Neuropsychologie zur Methode gehört. Ähnlich könnte man bei der expliziten Parallelisierung von beobachtbarem Verhalten und rein subjektiven Phänomenen vorgehen oder eine explizite Parallelisierung zwischen Aktivitäten von Gehirnzellen (oder auch anderer Zellen) mit rein subjektiven Phänomenen.

Die verhaltensbasierte empirische Psychologie hat in zahllosen Modellbildungen gezeigt, wie man auf der Basis von Verhaltensdaten empirisch kontrollierte Hypothesen über mögliche Verarbeitungsmechanismen im System formulieren kann. Wieweit diese Modelle sich im Rahmen von neuropsychologischen Studien in der Zukunft bestätigen lassen oder diese modifiziert werden müssen, das wird die Zukunft zeigen.

Abstraktionen – Allgemeinbegriffe

Wenn wir mittels sprachlicher Ausdrücke Gegenstände unserer Alltagswelt ansprechen, benutzen wir fast ausnahmslos sogenannte Allgemeinbegriffe. Ich frage nach der ‚Schüssel‘ wohl wissend, dass es hunderte von Gegenständen geben kann, die konkret verschieden sind, die wir aber alle als ‚Schüssel‘ bezeichnen würden; desgleichen mit Ausdrücken wie ‚Tasse‘, ‚Flasche‘, ‚Tisch‘, Stuhl‘, usw.

Indem wir sprachliche Ausdrücke benutzen machen wir stillschweigend Gebrauch von der Fähigkeit unseres Gedächtnisses, dass alles, was wir gegenständlich wahrnehmen, ‚verallgemeinert‘ wird, d.h. von Details abgesehen wird und Kerneigenschaften abstrahiert werden (die Philosophen sprechen auch von Kategorisierung, der Bildung von Kategorien; eine andere Bezeichnung ist das Wort ‚Klasse‘). Dies geschieht offensichtlich unbewusst, ‚automatisch‘; unser Gedächtnis arbeitet einfach so, stillschweigend, lautlos. Was immer wir wahrnehmen, es wird in ein abstraktes Konzept ‚übersetzt‘, und alles, was zukünftig diesem Konzept ‚ähnlicher‘ ist als anderen Konzepten, das wird dann diesem Konzept zugerechnet. Ein gedankliches Gegenstandskonzept kann auf diese Weise für viele hundert unterschiedliche konkrete Gegenstände stehen. Und die Sprache braucht immer nur ein einziges Wort für ein solches abstraktes Gegenstands-Konzept.

Im konkreten Fall (wie z.B. dem Essen) ist die Verständigung meist einfach, da vielleicht nur eine einzige Schüssel auf dem Tisch steht. Wenn nicht, dann haben diese Schüsseln eventuell eine unterscheidende Eigenschaft (anhand ihrer räumlichen Position, Farbe, Größe, Inhalt, …). Die Schüssel ’neben‘ …, die ‚rote‘ Schüssel…, die ‚kleine weiße Schüssel‘ …, die Schüssel mit dem Reis ….

Wenn wir den Interpretationsprozess genauer beschreiben wollen, dann müssten wir diese Abstraktionsprozesse und ihre Anwendung in die Theoriebildung mit einbeziehen.

Diese Abstraktionsprozesse finden wir nicht nur bei ‚Gegenständen‘, sondern auch bei der Lautwahrnehmung. Wen wir ein gesprochenes Wort wie ‚Tasse‘ hören, dann hören wir dieses gesprochene Wort auch dann, wenn es schneller, langsamer, höher, tiefer, lauter oder leiser usw. gesprochen wird. Alle diese verschiedenen Äußerungsereignisse sind physikalisch sehr unterschiedlich und die moderne Sprachtechnologie hat viele Jahrzehnte gebraucht, um ‚in den meisten Fällen‘ das ‚richtige‘ Wort zu erkennen. Wir Menschen gehen mit diesen vielen unterschiedlichen Realisierungen vergleichsweise mühelos um. Auch hier verfügt unser Wahrnehmungs- und Gedächtnissystem über sehr leistungsfähige Abstraktionsprozesse, die zur Ausbildung von Lautkategorien und dann Wortklassen führen.

Wechselwirkungen zwischen Kategorien und Sprache

Damit finden wir auf der untersten Ebene des sprachlichen Zeichengebrauchs zwei selbständige Abstraktions- und Kategoriensysteme (Laute, Gegenstände), die im Zeichengebrauch zusammen geführt werden. Bevor Kinder diese beiden Systeme nicht meistern, können sie nicht wirklich Sprache lernen. Wenn sie es aber geschafft haben, diese Laut- und Gegenstandskategorien in sich zu realisieren, dann explodiert ihr Sprachlernen. (Anmerkung: Für einen Überblick siehe: Language development. Besonders aufschlussreich sind die empirischen Daten zur Entwicklung der Lautbildung, des Bedeutungserwerbs und der Grammatik. Umfassendere Theoriebildungen sind meist sehr spekulativ.)

Eine oft diskutierte Frage ist, in wieweit die Kategorienbildung bei den Gegenständen unabhängig ist von der Korrelation mit den Laut- und Wortkategorien (Anmerkung: Siehe einen Überblick zum Streit über die Sapir-Whorf-Hypothese.). Sofern diese Abstraktionsprozesse in genetisch bedingten Verarbeitungsprozessen gründen (wie z.B. der Farbwahrnehmung) darf man davon ausgehen, dass die sprachlichen Besonderheiten diese grundsätzlichen Kategorienbildung im Gegenstandsbereich nicht verändern, höchstens unterschiedlich nutzen. Für das gemeinsame Erlernen von Sprache bildet die Unabhängigkeit der vorsprachlichen Kategorienbildung eine Voraussetzung, dass eine Sprache gelernt werden kann. Gibt es hier Abweichungen (Anmerkung: wie z.B. bei Farbblindheit, generell Sehstörungen oder gar Blindheit, bei Taubheit, bei Störungen der Sinneswahrnehmungen, usw.), dann wird das gemeinsame Erlernen von Sprache in unterschiedlichen Graden erschwert bzw. eingeschränkt.

Bedeutung als Werden

Man kann erkennen, dass schon auf dieser untersten Ebene des Sprachgebrauchs Menschen, obgleich sie das gleiche Wort benutzen (wie ‚Flasche‘, ‚Tasse‘, …), damit ganz unterschiedliche Dinge verbinden können, je nachdem welche konkreten Gegenstände sie im Laufe ihrer Lerngeschichte sie wahrnehmen konnten. Je weiter sich diese Gegenstände von einfachen Alltagsgegenständen entfernen und komplexere Gegenstände benennen wie Tätigkeiten (‚Autofahren‘, ‚Einkaufen‘, ‚Reparieren‘, ..), komplexe Situationen (‚Parkhaus‘, ‚Jahrmarkt‘, ‚Sportveranstaltung‘, …) oder komplexe Organisationen (‚Gemeindeverwaltung‘, ‚politische Partei‘, ‚Demokratie‘, …), umso vielfältiger und umso unschärfer (‚fuzzy‘) werden die damit eingeschlossenen konkreten Eigenschaften. So wunderbar die Verfügbarkeit von abstrakten Begriffen/ Klassen/ Kategorien/ Allgemeinbegriffen den Gebrauch von Sprache vereinfacht, so trügerisch können diese Begriffe sein. 10 Menschen benutzen das Wort ‚Gott‘ und jeder versteht damit möglicherweise etwas ganz anderes.

Der Aufbau einer gemeinsam geteilten Bedeutungswelt ist in keiner Weise ein ‚Selbstgänger‘; langer Atem, gemeinsame Anstrengungen, Abstimmungen, Abgleiche, viel Kommunikation ist notwendig, um Verstehen zu ermöglichen, Missverständnisse zu verringern und bewusster Manipulation entgegen zu treten.

Einen Überblick über alle Blogbeiträge des Autors cagent nach Titeln findet sich HIER.

GEMEINSAMKEIT IN DER VIELFALT – GRASWURZEL-/ BOTTOM-UP-PHILOSOPHIE – Memo zur philosophieWerkstatt vom 12.Okt.2014

Ähnliches, Allgemein, Alltag, Alltagssprache, Analytisch, Apriori, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Bedeutungsraum, Begriffe, Bewußtsein, Bibel, Bild im Kopf, Biologische Evolution, Philosophiewerkstatt, Semantik, Sozialer Druck, Sprache, Sprache und Denken, Sprachliche Äußerung, Sprachmaterial, Übertragung, Vorurteil, Vorwissen, Wahr, Wahrheit, Wahrheit - definitorische (analytische), Wahrheit - Frage nach, Wahrheit - ontologische, Wahrheitskriterium, Wahrnehmen, Wahrscheinlichkeit

Dieses Memo bezieht sich auf die philosophieWerkstatt v.2.0 vom 12.Okt.2014.

1. Ein neuer Ort, eine neue Zeit, neue Menschen …. die philosophieWerkstatt v2.0 ging an den Start und trotz schönem Wetter und vielen Grippeinfizierten gab es eine bunte Runde von Gesprächsteilnehmern die sich zu einem philosophischen Gespräch zusammen fanden.

2. In einer kleinen ‚Aufwärmphase‘ konnte jeder etwas von sich und seinen Erwartungen erzählen und es wurde ein erstes Begriffsfeld sichtbar, das von Vielfalt kündete und einen erkennbaren Zusammenhang noch vermissen lies (siehe nachfolgendes Bild).

Begriffe im Raum, unverbunden, der Anfang
Begriffe im Raum, unverbunden, der Anfang

3. Es stand die Frage im Raum, ob und wie man hier zu einem verbindlichen Zusammenhang kommen könne? Wie – hier vorgreifend auf das Ergebnis des Gespräches – das abschließende Gesprächsbild andeutet, kam es zu immer mehr Differenzierungen, wechselseitigen Abhängigkeiten, Verdichtungen und Abstraktionen, die – wenngleich noch zaghaft – eine erste Struktur andeuten, an der man bei einem Nachfolgegespräch weiter anknüpfen könnte.

Begriffe in einem beginnenden Zusammenhang, Umrisse einer Struktur
Begriffe in einem beginnenden Zusammenhang, Umrisse einer Struktur

BILDER VON DER WELT – BEDEUTUNG

4. Eine erste Wendung im Gespräch kam durch den Hinweis, dass die ‚Bedeutung‘, die wir von den ‚Ausdrücken‘ einer Sprache unterscheiden, ‚in unserem Kopf‘ zu verorten sei. Dort. ‚in unserem Kopf‘ haben wir ‚Bilder von der Welt‘ (‚Vorstellungen‘, ‚mentale Repräsentationen‘), die für uns ‚Eigenschaften der umgebenden Welt‘ repräsentieren.

VORWISSEN

5. Bald kam auch der Begriff des ‚Vorwissens‘, der ‚bisherigen Erfahrung‘, einer ‚Vorprägung‘ ins Spiel: gemeint war damit, dass wir in jedem Augenblick nicht vom Punkt Null beginnen, sondern schon Erfahrungen in der Vergangenheit gemacht haben, die auf die aktuelle ‚Wahrnehmung der Welt‘ einwirken: als ‚Erwartungen‘, als ‚Vor-Urteil‘, als ‚Übertragung‘.

SOZIALER DRUCK

6. Hier wurde auch darauf hingewiesen, dass die ‚Interpretation der Wahrnehmung‘ von anderen Menschen (‚Gruppenzwang‘, ‚gesellschaftliche Gewohnheiten/ Erwartungen‘, ‚Prüfungssituationen‘) zusätzlich beeinflusst werden kann. Während man normalerweise spontan (fast unbewusst) entscheidet, wie man eine Wahrnehmung interpretieren soll (obgleich sie vieldeutig sein kann), kann dieser Prozess unter sozialem Druck gestört werden; wie zögern, werden unsicher, bemerken, dass die Situation vielleicht nicht eindeutig ist, und suchen dann nach Anhaltspunkten, z.B. nach den Meinungen der anderen. Oft ist es so, dass die ‚Mehrheit‘ besser ist als die Meinung eines einzelnen; die Mehrheit kann aber auch völlig daneben liegen (berühmtes Galileo-Beispiel).

ÄHNLICHKEITEN ZWISCHEN PERSONEN

7. Die Frage war, wie es denn überhaupt zu ‚Ähnlichkeiten‘ zwischen Personen kommen kann, wenn jeder seine Bilder im Kopf hat?

8. Ein Schlüssel scheint darin zu liegen, dass jeder seine Bilder in seinem Kopf anlässlich der Gegebenheiten der umgebenden Welt ‚formt‘. Sofern die umgebende Welt für alle die ‚gleiche‘ ist, lässt sich von daher eine gewisse Ähnlichkeit der Bilder motivieren.

9. Zusätzlich gibt es aber auch die Sachlage, dass die Körper der Menschen mit ihren Organen und Prozessen, insbesondere mit ihrem Gehirn und den darauf basierenden Information verarbeitenden Prozessen, eine gewisse Ähnlichkeit zwischen allen Menschen aufweisen, so dass auch dadurch Ähnlichkeiten zwischen den Bildern im Kopf begünstigt werden.

BEGRENZUNG DES BEWUSSTSEINS

10. In der neuzeitlichen Orientierung am Bewusstsein als primärer Erkenntnisquelle (ungefähr seit Descartes und später bis zur Phänomenologie) gab es keine Ansatzpunkte, um diese implizite ‚Harmonie der Körper und Erkenntnisse‘ aufzuhellen. Die antike Philosophie – insbesondere Aristoteles und seine Schüler – hatte zwar Ansatzpunkte, die Erkenntnisse über die Welt einzubeziehen, aber die damaligen ‚Welterkenntnisse‘ reichten nicht aus, um das moderne empirische Wissen über die physikalische, chemische, biologische und kulturelle Evolution vorweg zu nehmen. Erst mit den neuen Wissenschaften und einer davon inspirierten Strömung einer ‚evolutionär inspirierten‘ Erkenntnistheorie und Philosophie lieferte erste sachdienliche Hinweise, dass die unübersehbare ‚Harmonie der Körper‘ auch ein Grund für die Ähnlichkeit zwischen den Bildern in den verschiedenen Köpfen sein kann.

SCHLÜSSEL EVOLUTION

11. Mehr noch, die verblüffende ‚Passung‘ von menschlicher Erkenntnis zur ‚umgebenden Welt‘ ist letztlich vollständig induziert von einer evolutionären Entwicklung, in der sich nur solche Organismen ‚durchsetzen‘ konnten, die relativ am besten die ‚lebensfördernden Eigenschaften‘ der umgebenden (aber auch in sich sich verändernden) Welt aufgreifen und nutzen konnten.

12. Wenn man davon sprechen kann, dass der Menschen ein ‚Ebenbild‘ sei, wie es biblische Texte nahelegen (hier ohne kritischen Kommentar), dann zunächst mal ein Ebenbild der vorgegebenen Erde als Teil eines Sonnensystems als Teil einer Galaxie als Teil eines BigBang-Universums (Weiterreichende Interpretationen sind damit per se noch nicht ausgeschlossen).

BILDER IM KOPF vs. WELT

13. Es wurde auch festgestellt, dass man zwischen den ‚Bildern von der Welt im Kopf‘ und den ’sprachlichen Ausdrücken‘ unterscheiden muss.

ALLGEMEINBEGRIFFE

14. Die ‚Bilder von der Welt‘ repräsentieren irgendwie (mal mehr, mal weniger ‚passend‘) die ‚Gegebenheiten‘ der umgebenden Welt. Dies geschieht durch eine ‚denkerische‘ Mixtur aus ’sinnlicher Erfahrung von Einzelnem‘ und ‚denkerischer Abstraktion von Allgemeinheiten‘, so dass wir in jedem Moment zwar einen einzelnen konkreten Gegenstand identifizieren können, zugleich aber auch immer einen ‚allgemeinen Begriff‘, eine ‚Kategorie‘ zur Verfügung haben, die anhand von ‚abstrahierten Eigenschaften‘ einzelne Gegenstände als ‚Beispiele‘ (‚Instanzen‘) einer allgemeinen Struktur erscheinen lässt. Unser Denken lässt gar nichts anderes zu; es ‚zwingt‘ uns zur ‚automatischen‘ (‚unbewussten‘) Konstruktion von ‚Allgemeinbegriffen‘.

SPRACHE UND DING

15. Es wurde darauf hingewiesen, dass wir ja auch verschiedene Sprachen sprechen und dass möglicherweise die ‚Bilder im Kopf‘ bis zu einem gewissen Grade unabhängig von der verwendeten Sprache sind. Deswegen können wir auch zwischen den Sprachen übersetzen! Weil die körpergebundenen Sachstrukturen – bis zu einem gewissen Grade – sprachunabhängig gegeben sind und sich ‚aufbauen‘, können die Ausdrücke einer Sprache L darauf Bezug nehmen und durch andere ‚bedeutungsgleiche‘ Ausdrücke ‚ersetzt werden.

VERÄNDERLICHE WELT vs. STATISCHE BILDER

16. Die ‚Bedeutung‘ sprachlicher Ausdrücke (ihre ‚Semantik‘) begründet sich also von den körperbedingten Objektstrukturen her. Wenn nun die umgebende Welt sich ändert (Prozess, Geschichte, Evolution, …), dann ändern sich zwar die Sachstrukturen in der Welt, nicht aber unbedingt synchron die Bilder im Kopf eines Menschen. Damit entsteht das, was wir oft erleben: Menschen benutzen Ausdrücke einer Sprache L, ‚Begriffe‘, ‚Termini‘, die sie mit bestimmten ‚Bildern im Kopf‘ verknüpfen (assoziieren), aber diese Bilder können ‚veraltet‘ sein, da sich die Gegebenheiten in der Welt mittlerweile verändert haben (im Gespräch wurde der Ausdruckswandel des Begriffs ‚Student‘ angesprochen).

EINFACH vs. KOMPLEX

17. Vor dem Hintergrund einer ‚erlernten‘ Bedeutung kann es dann passieren, dass die ‚erlernten‘ Bedeutungen aus einer früheren Zeit die Welt ‚einfacher‘ erscheinen lassen als die gegenwärtige Welt mit ihrer wachsenden Vielfalt (es standen die Bemerkungen im Raum, dass Mädchen und junge Frauen es früher ‚einfacher‘ gehabt haben sollen als Mädchen und junge Frauen heute).

WAS IST WAHRHEIT?

18. An diesem Punkt im Gespräch angekommen stellte sich nochmals die Frage nach der ‚Wahrheit‘, ein Begriff, der ganz am Anfang etwas isoliert im Raum stand.

19. Ausgangspunkt ist die alltägliche Beobachtung, dass wir manchen Aussagen als ‚richtig‘, manche als ‚falsch‘ bezeichnen. Dies knüpft an dem Umstand an, dass ‚Behauptungen über die Gegebenheiten der Welt‘ bis zu einem gewissen Grade ‚überprüfbar‘ sind. D.h. es scheint, dass wir die ‚Bilder in unserem Kopf‘ mit den sinnlich wahrnehmbaren Gegebenheiten der umgebenden Welt bis zu einem gewissen Grad so ‚vergleichen‘ können, dass wir eine ‚Übereinstimmung‘ oder ‚Nicht-Übereinstimmung‘ feststellen können, und zwar alle Menschen in gleicher Weise.

20. Wenn wir diesen grundsätzlichen Sachverhalt zum Ausgangspunkt nehmen, dann würde der Begriff ‚Wahrheit‘ in diesem Kontext bedeuten, dass eine Aussage mit ’sinnlicher Bestätigung‘ sowohl ‚richtig‘ als auch ‚wahr‘ wäre bzw. — falls keine Übereinstimmung vorliegt –, ’nicht richtig‘ bzw. ‚falsch‘ bzw. ’nicht wahr‘ wäre.

21. Bei diesem Interpretationsansatz werden damit die ‚Gegebenheiten der Welt‘ zum Ausgangspunkt, zur ‚Vorgabe‘, zum ‚Maßstab‘, an dem wir uns letztlich orientieren. Davon abgeleitet könnte man dann auch – ganz im Sinne der antiken Metaphysik und Ontologie – davon sprechen, dass ‚das Seiende‘, wie es uns – in gewissem Sinne ‚a priori‘ – vorgegeben ist, das ‚Wahre‘, die ‚Wahrheit‘ verkörpert, an der wir uns orientieren müssen, wollen wir im Sinn der Welt/ des Sonnensystems/ der Galaxie/ des BigBang-Universums/ des … ‚wahr‘ sein. Empirische Wissenschaft ist dann nichts anderes als antike Metaphysik (dafür gäbe es noch mehr Argumente).

22. Eine solcherart (ontologisch) verstandene Wahrheit ist dann nicht beliebig, sondern eher ‚verpflichtend‘: wer das ‚Leben‘ ‚achtet‘ und ‚liebt‘ muss sich eigentlich an dieser Wahrheit orientieren. Dies wäre damit auch die mögliche Begründung einer ‚Ethik des Lebens‘, die sich z.B. als ‚ökologisches Denken‘ manifestiert.

ANALYTISCH WAHRHEIT

23. Wenn wir annehmen, dass wir zu einem bestimmten Zeitpunkt ‚Bilder im Kopf‘ von der umgebenden Welt haben und wir diese Bilder als ‚zutreffen‘ – sprich als ‚wahr‘ – betrachten, dann können wir oft auch auf der Basis dieser vorausgesetzten Bilder ‚Schlüsse ziehen‘. Berühmt sind die Beispiele mit Syllogismen wie (Annahme 1) ‚Alle Menschen sind sterblich‘, (Annahme2:) ‚Sokrates ist ein Mensch‘, (Schluß:) ‚Sokrates ist sterblich‘. Nimmt man an, dass Annahme 1 und 2 ‚wahr‘ sind, dann folgt ‚analytisch‘ (ohne Bezug auf die aktuelle empirische Welt), der Schluss. Die Wissenschaft der Logik arbeitet im Prinzip nur mit solchen analytischen Schlüssen und ihren möglichen (formalen) Formen. Sie weiß als Wissenschaft der Logik nichts von der Welt (was sich auch darin auswirkt/ auswirken kann, dass sie formale Strukturen entwickelt, die mehr oder weniger ‚unbrauchbar‘ für das weltbezogene Alltagsdenken sind).

ALLE SIND TRÄGER DER WAHRHEIT

24. Rückblickend zu diesem Gespräch kann man also sagen, dass letztlich jeder Stücke der allgemeinen Wahrheit mit sich herum trägt und dass es eigentlich nur darauf ankommt, diese einzelnen Fragmente zusammen zu sammeln und sie in rechter Weise ‚zusammen zu fügen’… Graswurzel-Philosophie … Bottom-Up Philosophie … induktives Denken …

Die Ankündigung zur nächsten Sitzung am 9.Nov.2014 findet sich HIER.

Für einen Überblick über alle Blogeinträge zur Philosophiewerkstatt siehe HIER

Für einen Überblick über alle Blogeinträge nach Titeln siehe HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15

Analytisch, Art (Spezies), Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - akzidentell, Bedeutung - empirisch, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsraum, Definition, Definition - explitite, Definitorisch, Eigenschaft, Externe Welt, Falsch, Gattung (genus), Kategorien, Kognition, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Logische Operatoren, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt - kontingent, Objekt - universell, Objekthierarchie, Objekttyp, Ontologie, ontologisch, Operator, Operator - aussagenlogischer, Prädikat, Proposition, Sein, Semantik, Subjekt, Subjekt - logisches, Wahr, Wahrheit, Wahrheit - definitorische (analytische), Wahrheit - ontologische, Wahrheit als Übereinstimmung, Wahrheitsbegriff, wahrheitsfähig, Wahrheitsgehalt, Wahrheitskriterium, Wahrheitswert

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M
Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M

WAHR UND FALSCHE AUSSAGEN

1. Nach dem Blogeintrag Avicenna 14b gibt es jetzt Ausdrücke A, B, …, die ‚wahr‘ oder ‚falsch‘ sein können und die wir deshalb ‚Aussagen‘ (auch ‚Propositionen‘) nennen. Aussagen können mittels aussagenlogischer Operatoren wie ‚NEGATION‘, ‚UND‘, ‚IMPLIKATION‘ usw. zu komplexeren Ausdrücken so verknüpft werden, dass jederzeit ermittelt werden kann, wie der Wahrheitswert des komplexen Ausdrucks lautet, wenn die Wahrheitswerte der Teilausdrücke bekannt sind. Ob im Einzelfall eine Aussage A ‚wahr‘ oder ‚falsch‘ ist, muss durch Rückgriff auf ihre Bedeutungsbeziehung M(A) geklärt werden. Bislang ist nur klar, dass die Bedeutungsbeziehung M nur allgemein eine Beziehung zu den (kognitiven) Objekten O herstellt (siehe Grafik oben).

2. Avicenna spricht aber nicht nur von Aussagen A allgemein, sondern unterscheidet die Teilausdrücke ‚Subjekt‘ S und ‚Prädikat‘ P, zusätzlich oft noch ‚Quantoren‘ Q.

FEINSTRUKTUR DER BEDEUTUNG VON AUSDRÜCKEN

3. Man kann und muss dann die Frage stellen, ob und wie sich auf der Bedeutungsseite die Unterscheidung in S und P auf der Ausdrucksseite widerspiegelt?

ECHTE UND UNECHTE OBJEKTE

4. In vorausgehenden Blogeinträgen zu Avicenna (Avicenna 4, 5, 7 und 11) wurde schon unterschieden zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte Objekte‘ sind solche Wissenstatbestände, die man zwar identifizieren und unterscheiden kann, die aber immer nur im Kontext von ‚echten Objekten‘ auftreten. ‚Unechte‘ Objekte werden meistens als ‚Eigenschaften‘ bezeichnet. Beispiel: die Farbe ‚Rot‘ können wir wahrnehmen und z.B. von der Farbe ‚Blau‘ unterscheiden, die Farbe ‚Rot‘ tritt aber nie alleine auf so wie z.B. Gegenstände (Tassen, Stühle, Früchte, Blumen, …) alleine auftreten.

5. Hier wird davon ausgegangen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf.

GATTUNG UND ART; KATEGORIEN

6. Ein Objekt kann viele Eigenschaften umfassen. Wenn es mehr als ein Objekt gibt – also O1, O2, … — die sowohl Eigenschaften Ex gemeinsam haben wie auch Eigenschaften Ey, die unterschiedlich sind, dann kann man sagen, dass alle Objekte, die die Eigenschaften Ex gemeinsam haben, eine ‚Gattung‘ (‚genus‘) bilden, und dass man anhand der ‚unterscheidenden Eigenschaften Ey‘ unterschiedliche ‚Arten‘ (’species‘) innerhalb der Gattung unterscheiden kann.

7. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden.

ONTOLOGISCHE UND DEFINITORISCHE (ANALYTISCHE) WAHRHEIT

8. Bislang ist der Wahrheitsbegriff $latex \top, \bot$ in dieser Diskussion an der hinreichenden Ähnlichkeit eines vorgestellten/ gedachten kognitiven) Objekts $latex a \in Oa$ mit sinnlichen wahrnehmbaren Eigenschaften $latex s \subseteq Os$ festgemacht worden. Ein ‚rein gedachtes Objekt $latex a \in Oa$ ist in diesem Sinne weder ‚wahr‘ $latex \top$ noch ‚falsch‘ $latex \bot$.

9. Setzt man allerdings eine Objekthierarchie O voraus, in der man von einem beliebigen individuellem Objekt a immer sagen kann, zu welchem Objekt Y es als seiner Gattung gehört, dann kann man eine Aussagen der Art bilden ‚a ist eine Tasse‘.

10. Wenn man zuvor in einer Definition vereinbart haben sollte, dass zum Begriff der ‚Tasse‘ wesentlich die Eigenschaften Ex gehören, und das Objekt a hätte die Eigenschaften $latex Ex \cup Ey$, dann würde man sagen, dass die Aussage ‚a ist eine Tasse‘ ‚wahr‘ ist, unabhängig davon, ob es zum kognitiven Objekt a ein ’sinnliches‘ ‚Pendant‘ geben würde oder nicht. Die Aussage ‚a ist eine Tasse‘ wäre dann ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr.

11. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a, die als solche nichts darüber sagt, ob es das Objekt a ‚tatsächlich‘ gibt, soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden, also einer Wahrheit, die sich auf das ‚real Seiende‘ in der umgebenden Welt W bezieht.

12. [Anmerkung: Dieses – auch im Alltagsdenken – unterstellte ‚Sein‘, die unterstellte übergreifende ‚Realität‘ ist nicht nur eine ‚Extrapolation‘ aufgrund sinnlicher Gegebenheiten ‚im‘ wissenden System, sondern ist in seiner unterstellten ‚Realität‘ auch nur eine sehr spezifische Form von Realität. Wie wir heute aufgrund immer komplexerer Messprozeduren wissen, gibt es ‚Realitäten‘, die weit jenseits aller sinnlichen Qualitäten liegen. Es fällt uns nur nicht so auf, weil diese gemessenen Eigenschaften X durch allerlei Prozeduren für unsere Sinnesorgane ‚umgerechnet‘, ‚transformiert‘ werden, so dass wir etwas ‚Sehen‘ oder ‚Hören‘, obgleich das gemessene X nicht zu sehen oder zu hören ist.]

13. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘).

14. Derjenige Ausdrucksteil As, der sich auf das echte Objekt a bezieht, ‚von dem‘ etwas ausgesagt werden soll (‚ist ein…‘, ‚hat …‘), dieser Ausdrucksteil wird als ‚Subjekt‘ S bezeichnet, und der Ausdrucksteil Ap, mittels dem etwas über das Subjekt ausgesagt wird, wird ‚Prädikat‘ P genannt.

15. Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. [Anmerkung: Bei ’neuronalen Netzen‘ wäre das R-Objekt jenes Neuron, das die Verbindung zwischen zwei anderen Neuronen ‚realisiert‘.]

17. Fassen wir zusammen: Bei einem Ausdruck A der Art A=’Hans ist ein Mensch‘ gibt es den Ausdrucksteil As=’Hans‘ und den Ausdrucksteil Ap=’ist ein Mensch‘. Die Bedeutung des Ausdrucksteils As M(As) als M(‚Hans‘) ist ein Objekt h in der unterstellten Bedeutungshierarchie O des Sprechers, das gewisse Eigenschaften E(h) besitzt. Die Bedeutung des Ausdrucksteils Ap als M(Ap) bzw. M(‚ist ein Mensch‘) ist sowohl ein Objekt M mit Eigenschaften E(M) als auch eine Beziehung R_ist zwischen dem Objekt h und dem Objekt M, also R_ist(h,M). Die Beziehung ist definitorisch/ analytisch ‚wahr‘ wenn es gilt, dass die definierenden Eigenschaften E(M) des Objekts Mensch M auch bei den Eigenschaften E(h) von Hans zu finden sind, also $latex E(M) \subset E(h)$ .

BEZIEHUNGSRAUM – TRANSZENDENTALE BEDINGUNGEN

18.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14

Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - empirisch, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Bedeutungsraum, Erfüllung, Falsch, Logik, Logik - Alltag, Logik - Antike, Logische Operatoren, Möglichkeit, Notwendig, Operator, Operator - aussagenlogischer, Semantik, Wahr, Wahrheit, Wissen, Wissen - gefolgertes, Wissen - sensorisches, Wissen - sprachlich vermitteltes, Zutreffen

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

1. Wenn also eine Formulierung von Konvertierungsregeln nicht ohne Bezug auf irgend eine Bedeutung M hinter den Ausdrücken möglich ist, stellt sich zum wiederholten Male die Frage, über welche mögliche Bedeutung M ‚hinter‘ den Ausdrücken gesprochen werden muss.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

2. Beginnen wir mit dem Ausgangspunkt, dass Aussagen PROP solche Ausdrücke von der Menge aller Ausdrücke E sind, die ‚wahr‘ oder ‚falsch‘ sein können. ‚Treffen sie zu‘ gelten sie als ‚wahr‘; ‚treffen sie nicht zu‘ gelten sie als ‚falsch‘.
3. Bislang hatten wir schon die generelle Annahme geäußert, dass das Denken und Wissen eines Menschen im ‚Innern‘ dieses Menschen zu verorten sei und der Mensch ‚in‘ einer umgebenden Welt W mit realen Ereignissen X vorkommt.
4. Um die Begriffe ‚wahr/ falsch‘ bzw. ‚zutreffen/ nicht zutreffen‘ zu ‚erklären‘, nehmen wir an, dass die Menge des möglichen Wissens K eines einzelnen Menschen sich zerlegen lässt in die Teilmengen ‚Vorgestellt‘ K_v, ‚Erinnert‘ K_m sowie ’sinnlich präsent‘ K_s. Es gilt also $latex K = K_{s} \cup M_{v} \cup M_{m}$.
5. Eine Bedeutung wird dann durch eine Beziehung zwischen dem Wissen K und möglichen Ausdrücken $latex PROP \subseteq E$ gebildet: $latex M \subseteq PROP \times K$.
6. Speziell gilt aber, dass man zwischen einer ’neutralen‘ Bedeutung $latex M_n \subseteq E \times (K_{v} \cup K_{m})$ unterscheiden muss, die weder ‚wahr‘ noch ‚falsch‘ ist, und der ’sinnlich fundierten‘ Bedeutung $latex M_s \subseteq E \times K_{s}$. Gibt es zwischen einer neutralen Bedeutung $latex M_{n}$ und einer sinnlich fundierten Bedeutung $latex M_{s}$ eine Beziehung des ‚Zutreffens‘ $latex M_{s} \models M_{n}$, dann kann man sagen, dass das Wissen $latex K_{n}$ in dieser Beziehung ‚wahr‘ ist, andernfalls nicht, geschrieben $latex M_{s} \not\models K_{n}$.
7. Zusätzlich kann man im Bereich des erinnerten Wissens $latex K_{m}$ noch unterscheiden zwischen einem solchen, das Bezug zu ‚vormals sinnlich fundiertem Wissen‘ aufweist als $latex K_{ms}$ und solchem, das ‚keinen Bezug zu vormals fundiertem sinnlichen Wissen‘ aufweist als $latex K_{mns}$.
8. Erinnertes Wissen mit Bezug zu vormals fundiertem Wissen $latex K_{ms}$ hat die Eigenart, dass sich in Abhängigkeit von der ‚Häufigkeit‘ der erinnerbaren Wissenselementen in $latex K_{ms}$ eine Art ‚Erwartung‘ bzgl. des neuerlichen Eintretens dieses Wissens als sinnliches Wissen $latex K_{vs}$ ausbildet: $latex \mu: K_{ms} \longrightarrow K_{vs}$ mit $latex K_{vs} \subseteq K_{v}$, d.h. im Bereich des vorgestellten Wissens $latex K_{v}$ gibt es solches mit einem speziellen Erwartungsanteil $latex K_{vs}$ hervorgerufen durch besondere Erinnerungen.

EXKLUSIVE MODALOPERATOREN

9. An dieser Stelle könnte man dann noch die Begriffe ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ wie folgt einführen: ein vorgestelltes Wissen gilt als ‚möglich‘, wenn der Erwartungswert nicht gleich 1 ist, also $latex \diamond K_{v} \leftrightarrow \mu(K_{v}) \not= 1$, andernfalls als notwendig, also $latex \boxempty K_{v} \leftrightarrow \mu(K_{v}) = 1$
10. Daraus kann man ableiten, dass gelten soll $latex \boxempty K_{v} \leftrightarrow \neg\diamond K_{v}$ oder $latex \neg\boxempty K_{v} \leftrightarrow \diamond K_{v}$.
11. Diese Definition von ‚möglich‘ und ’notwendig‘ entspricht nicht ganz der ‚Intuition‘, dass etwas, was ’notwendig‘ ist, auf jeden Fall auch möglich sein sollte; allerdings folgt – intuitiv — aus der Möglichkeit keine Notwendigkeit. Die vorausgehende Definition von möglich und notwendig erinnert ein wenig an das ‚exklusive Oder‘, das auch ’schärfer‘ ist als das normale Oder. Nennen wie die hier benutzte Definition von ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ daher auch die ‚exklusiven Modaloperatoren‘: Wenn etwas notwendig ist, dann ist es nicht möglich, und wenn etwas möglich ist, dann ist es nicht notwendig.
12. Anmerkung: wenn etwas ‚gedanklich notwendig‘ ist, folgt daraus in diesem Rahmen allerdings nicht, dass es auch tatsächlich sinnlich eintritt. Aus der gedanklichen Notwendigkeit folgt nur, dass es in der erinnerbaren Vergangenheit bislang immer eingetreten ist und daher die Erwartung sehr hoch ist, dass es wieder eintreten wird.

WAHR und FALSCH ABKÜRZUNGEN

13. Wenn man von einer Aussage $latex e \in E$ sagen kann, dass das zugehörige vorstellbare Wissen $latex M(e)=K_{v}$ ‚wahr‘ ist, weil es auf ein sinnliches Wissen $latex K_{s}$ ‚zutrifft oder eben ‚falsch‘, weil es ’nicht zutrifft‘, dann soll dieser Sachverhalt hier wie folgt abgekürzt werden:
14. Eine Aussage A soll genau dann mit ‚wahr‘ $latex \top$ bezeichnet werden, wenn es ein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\top \leftrightarrow M(A)=K_{v}$ und es gibt ein sinnlich fundiertes Wissen $latex K_{s}$, so dass gilt $latex K_{s} \models K_{v}$.
15. Eine Aussage A soll genau dann mit ‚falsch‘ $latex \bot$ bezeichnet werden, wenn es kein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\bot \leftrightarrow M(A)=K_{v}$ und $latex K_{s} \not\models K_{v}$. [Anmerkung: Es gibt nur ein einziges sinnlich fundiertes Wissen, und zwar das jeweils aktuelle!]

AUSSAGEOPERATOREN

16. Jetzt kann man folgende Operatoren über Aussagen definieren:
17. NEGATION: die Verneinung einer Aussage A ist wahr, wenn die Aussage selbst falsch ist, also $latex (\neg A)\top \leftrightarrow (A)\bot$.
18. KONJUNKTION: die Konjunktion $latex \wedge$ von zwei Aussagen A und B ist wahr, wenn beide Aussagen zugleich wahr sind; ansonsten ist die Konjunktion falsch, also $latex (A \wedge B)\top \leftrightarrow (A)\top\ und\ zugleich\ (B)\top$; ansonsten falsch.
19. DISJUNKTION: die Disjunktion $latex \vee$ von zwei Aussagen A und B ist wahr, wenn eine von beiden Aussagen wahr ist; ansonsten ist die Disjunktion falsch, also $latex (A \vee B)\top \leftrightarrow (A)\top\ oder\ (B)\top$; ansonsten falsch.
20. EXKLUSIVE DISJUNKTION: die exklusive Disjunktion $latex \sqcup$ von zwei Aussagen A und B ist wahr, wenn genau eine von beiden Aussagen wahr ist; ansonsten ist die exklusive Disjunktion falsch, also $latex (A \sqcup B)\top \leftrightarrow\ Entweder\ (A)\top\ oder\ (B)\top$; ansonsten falsch.
21. IMPLIKATION: die Implikation $latex \rightarrow$ von zwei Aussagen A und B ist wahr, wenn nicht A wahr ist und zugleich B falsch, also $latex (A \rightarrow B)\top \leftrightarrow\ nicht (A)\top\ und\ zugleich\ (B)\bot$; ansonsten falsch.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13

Allquantor, Avicenna, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Beweis - logischer, Falsch, Folgern - logisches, Konvertierung von Ausdrucksformen, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Partikularquantor, Prädikat, Quantor, Quantor - partikulär, Quantor - universell, Semantik, Subjekt, Wahr, Wahrheit

(Letzte Änderung 8.Sept.2014, 02:59h)

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

AVICENNAS DISKUSSION VON UMWANDLUNG (‚Conversion‘)

1. Aus der englischen Übersetzung ist nicht klar zu entnehmen, ob der Begriff ‚Umwandlung‘ (engl.: ‚conversion‘) tatsächlich eine Form von ‚Umwandlung’/ ‚Umformung’/ ‚Konvertierung‘ meint oder spezieller eine Umformung von Aussagen, die letztlich eine ‚logische Folgerung‘ darstellen. Letztere Interpretation wird angeregt, da er dann tatsächlich an entscheidender Stelle zum ersten Mal in der ganzen Abhandlung eine Folge von Aussagen präsentiert, die man als ‚Folgerungstext‘ interpretieren kann.

2. In seiner Kerndefinition gleich zu Beginn charakterisiert er den Ausdruck ‚Umformung‘ mit Bezug auf zwei Ausdrücke A und B, die Subjekte, Prädikate, Antezedenz und Konsequenz enthalten können (implizit auch Quantoren, da er diese im folgenden Text beständig benutzt). Jede der beiden Aussagen hat eine Bedeutung M(A) bzw. M(B). Umformung hat jetzt damit zu tun, dass einzelne dieser logischen Rollen (Q, S, P, …) ‚ausgetauscht‘ werden, ohne dass dadurch die ‚Bedeutung‘ verändert wird.

3. [Anmerkung: Hier gibt es folgende Unklarheiten: (i) Sollen die Bedeutungen M(A) und M(B) von vornherein ‚gleich‘ sein, und zwar so, dass sie nach dem Austausch unverändert sind? oder (ii) sind die Bedeutungen M(A) und M(B) von vornherein ungleich, sollen aber, jede für sich, auch nach der Umformung gleich sein? In beiden Fällen – so interpretiere ich seine Aussage von Avicenna, gibt es eine Bedeutung vor der Umformung – eine gemeinsame oder eine individuelle –, die nach der Umformung ‚gleich‘ geblieben ist. Schreiben wir für die Umformung als $latex \vdash$, dann würde bedeuten ‚$latex A \vdash B$‘ A wird nach B umgeformt, so dass die Bedeutung von A und B – gemeinsam oder individuell – erhalten bleibt. Es stellt sich hier wieder das Problem – wie im gesamten vorausgehenden Text –, dass der Begriff ‚Bedeutung‘ bei Avicenna nicht scharf definiert ist. Er kann alles und nichts bedeuten. Die ‚Gleichheit‘ von zwei Bedeutungen M_vorher und M_nachher ist also ein ‚offener Begriff‘.]

4. In dem folgenden Text präsentiert Avicenna einerseits einige Beispiele von Umformungen ohne genauere Begründungen, in einem Fall präsentiert er aber das Beispiel einer ausführlicheren Begründung, die wie eine Folgerungstext (wie ein logischer Beweis) aussieht. Beginnen wir mit den Beispielen ohne Begründung.

5. Mögliche Konversion: Von ‚Kein Mensch ist unsterblich‘ ($latex \neg\exists (Mensch)(ist)(unsterblich)$) kann man bedeutungserhaltend umformen in ‚Kein Unsterblicher ist ein Mensch‘ ($latex (\neg\exists (Unsterblicher)(ist)(Mensch)$).

6. Avicenna stellt die Regel auf: Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

7. Beispiel: Von ‚Jeder Mensch ist ein Lebewesen‘ kann ich nicht umformen zu ‚Jedes Lebewesen ist ein Mensch‘ (mehr formalisiert: ($latex \forall (Mensch)(ist)(Lebwesen)$) kann nicht umgeformt werden zu ($latex \forall (Lebewesen)(ist)(Mensch)$).

8. Avicenna stellt die Regel auf: Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

9. Beispiel: Die Aussage ‚Alle F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: Den Ausdruck $latex \forall (F)(sind)(B)$) kann man umformen zu ($latex \exists(B)(ist)(F)$))

10. Avicenna stellt die Regel auf: Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

11. Beispiel: Der Ausdruck ‚Einige F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: ($latex \exists (F)(sind)(B)$) $latex \vdash$ ($latex \exists (B)(sind)(F)$)).

12. Avicenna stellt die Regel auf: Eine negative Partikular-Aussage kann nicht konvertiert werden.

13. Beispiel: Die Aussage ‚Kein Lebewesen ist ein Mensch‘ kann nicht konvertiert werden zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

14. [Anmerkung: Hier gibt es einigen Diskussionsbedarf. Bevor die Diskussion eröffnet wird, hier aber noch das Konvertierungsbeispiel, das wie ein Folgerungstext aussieht.]

15. Ausgangspunkt ist die Regel: Eine negative All-Aussage kann in eine negative All-Aussage konvertiert werden mit dem Beispiel: Von ($latex \neg\exists (Mensch)(ist)(Unsterblicher)$) $latex \vdash$ ($latex \neg\exists (Unsterblicher)(ist)(Mensch)$).

16. Avicenna nennt die nun folgende ‚Folge von Aussagen‘ explizit einen ‚Beweis‘ (engl.: ‚proof‘).

17. Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F). Andernfalls [wäre der Wenn-Dann-Zusammenhang nicht wahr] würde der Widerspruch (engl.: ‚contradictory‘) folgen (Einige B sind F).

18. [Anmerkung: Zur Erinnerung, die Negation einer Implikation (Wenn A dann B) ist nur wahr, wenn A wahr wäre und zugleich B falsch, also ’nicht B‘, d.h. ’nicht(Kein B ist F)‘ d.h. (einige B sind F). Insofern bildet die Aussage (Einige B sind F) einen logischen Widerspruch zu (Kein B ist F). ]

19. Der Beweis beginnt damit, dass Avicenna eine Abkürzung einführt: Er definiert ‚H := ‚Einige B‘. [ein sehr gefährliches Unterfangen…]

20. Dann folgert er ‚H ist gleichbedeutend mit F‘

21. Er folgert weiter: ‚H ist sowohl F als auch B [Damit unterschlägt er, dass H eigentlich nur ‚einige‘ B meinen sollte]

22. Er folgert weiter: Dann gibt es ein F, das auch B ist ($latex \exists (F)(ist)(B)$

23. Er folgert weiter: Nehme ich die Aussage (Einige B sind F) als wahr an, dann komme ich zu der Aussage (Einige F sind B); dies steht aber im Widerspruch zu der Ausgangsbehauptung, das ‚Kein F ist B‘.

24. Er folgert weiter: Deshalb ist es nicht möglich, von der Ausgangsbehauptung ‚Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F)‘ auf den Widerspruch ‚Einige F sind B‘ zu schließen.

25. Avicenna folgert weiter: Von daher, wenn es gilt, dass ‚Kein F ist B‘, dann gilt auch die Konvertierung ‚Kein B ist F‘.

DISKUSSION

KONVERTIERBARKEIT DER FORMEN (Q (A B)) zu (Q (B A)) – BEDEUTUNGSABHÄNGIG

26. In den Beispielen, die Avicenna präsentiert, gibt es zwei Beispiele, die verwirrend sind. Im einen Fall will er über ’negative All-Aussagen‘ ($latex \neg\forall$) sprechen und im anderen Fall über ’negative Partikular-Aussagen‘ ($latex \neg\exists$). Das Beispiel für negative All-Aussagen lautet ‚Kein Mensch ist unsterblich‘. Der Quantor ‚kein‘ ist aber definiert als ’nicht einige‘ bzw. ‚$latex \neg\exists$‘. Dies aber ist gleichbedeutend mit einer negativen Partikular-Aussage. Später präsentiert er als Beispiel für negative Partikular-Aussagen den Ausdruck ‚Kein Lebewesen ist ein Mensch‘ ($latex \neg\exists (Lebewesen)(ist)(Mensch)$).

27. Damit haben wir es mit folgenden Widersprüchlichkeiten zu tun: (i) Avicenna interpretiert seinen Begriff der negativen Allaussagen mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert; (ii) Mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert, argumentiert er, dass man bedeutungserhaltend negative All-Aussagen konvertieren kann; (iii) Mit einem anderen Beispiel einer negativen Partikularaussage argumentiert er, man könne dieses nicht konvertieren.

28. Da das Beispiel zu (ii) zeigt, dass man sehr wohl eine negative Partikular-Aussage konvertieren kann, fragt man sich, warum es in einem anderen Fall nicht gehen soll. Dazu kommt, dass das konkrete Beispiel, das Avicenna präsentiert, aus sich heraus fragwürdig erscheint: ‚Kein Lebewesen ist ein Mensch‘ soll nicht konvertierbar sein zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

29. Bekannt ist – zumindest bezogen auf diese Begriffe –, dass sehr wohl einige Lebewesen Menschen sind, also eher gilt $latex \neg\neg\exists (Lebewesen)(ist)(Mensch)$, d.h. $latex \exists (Lebewesen)(ist)(Mensch)$. Von einer Aussage wie $latex \neg\exists (Mensch)(ist)\neg(Lebewesen)$) könnte man allerdings nicht konvertieren zu $latex \neg\exists (Lebewesen)(ist)\neg(Mensch)$).

30. Trotzdem gibt es eine mögliche Konvertierung von ($latex \neg\exists (Mensch)(ist)(Unsterblich)$)) zu ($latex \neg\exists (Unsterblich)(ist)(Mensch)$)).

31. Diese Beispiele legen die Vermutung nahe, dass die bisherigen ‚Konvertierungsregeln‘ von Avicenna nicht unabhängig sind von der jeweils unterstellten Bedeutung der beteiligten Subjekte und Prädikate.

32. Bezogen auf die Struktur (Q (A B)) $latex \vdash (Q (B A))$ hängt die Möglichkeit oder Unmöglichkeit einer Konvertierung in den Beispielen davon ab, wie sich die Bedeutungen von A und B, also M(A) und M(B), zueinander verhalten.

33. Zwei Hauptfälle kann man unterscheiden: (i) die Bedeutung von beiden Ausdrücken ist ‚gleich‘, d.h. M(A) = M(B), oder (ii) die Bedeutungen sind ungleich in dem Sinne, dass zwar alle Elemente, die zu M(B) gehören auch in M(A) sind, aber nicht umgekehrt, also $latex M(B) \subseteq M(A)$.

34. Wenn wir Fall (i) M(A) = M(B) unterstellen können, dann kann man von $latex \forall A sind B$ auf $latex \forall B sind A$ schließen, oder $latex \exists A sind B$ und umgekehrt. Die Aussage $latex \neg\forall A sind B$ wäre formal zwar möglich, wäre aber ’semantisch‘ (aufgrund der angenommenen Bedeutung) aber nicht möglich. Genau sowenig wie $latex \neg\exists A sind B$ semantisch möglich wäre, wohl aber syntaktisch.

35. Unterstellen wir hingegen den Fall (ii) $latex M(B) \subseteq M(A)$, dann würde die Konvertierung von $latex \forall A sind B$ auf $latex \forall B sind A$ nicht gelten. Entsprechend kann man die wahre Aussage $latex \forall B sind A$ nicht konvertieren zu $latex \forall A sind B$. Die Konvertierung $latex \exists A sind B$ würde gehen wie auch umgekehrt. Die Aussage $latex \neg\forall A sind B$ ist wahr, die Konvertierung zu $latex \neg\forall B sind A$ wäre falsch. Usw.

36. Diese Beispiele verdeutlichen, dass die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) zu (Q (B A)) eindeutig von der angenommenen Bedeutungsstruktur abhängig ist (zumindest in dem Kontext, den Avicenna diskutiert). Betrachten wir seine anderen Konvertierungsregeln.

37. (i) Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

38. (ii) Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

39. (iii) Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

40. (iv) Eine negative Partikular-Aussage kann nicht konvertiert werden.

41. Zu (i): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel nicht.

42. Zu (ii) und (iii): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel auch.

43. Zu (iv): Dieser Fall ist von der Form her (rein syntaktisch) möglich, von der Bedeutung her (rein semantisch) aber ausgeschlossen.

44. Bei allen bisherigen Konvertierungsbeispiele von Avicenna ist zu beachten, dass sich die Bedeutung des Subjekts S und des Prädikats P in einer Aussage (S P) in der Art $latex M(A) = M(B)$ oder $latex M(B) \subseteq M(A)$ beschreiben lässt. Dies setzt voraus, dass sich ein Prädikat P auch als eine Menge von Objekten auffassen lässt, denen eine bestimmte Eigenschaft E zukommt, also etwa P := ‚eine Menge von Elementen, die die Eigenschaft P haben‘. Zu sagen ‚S ist P‘ würde dann sagen, dass die Elemente die S sind auch die Elemente sind, die P sind.

45. Man muss hier die Frage stellen, ob Prädikate immer diese Form haben.

KONVERTIERUNG OHNE BEDEUTUNG?

46. Macht man die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) und (Q (B A)) von der Bedeutung M der Ausdrücke A und B abhängig, dann hängt die Formulierung der Konvertierungsregeln ab von einer brauchbaren Definition des zugrundeliegenden Bedeutungsraumes samt seiner Interaktion mit den Ausdrucksformen. Im weiteren Verlauf soll dies explizit untersucht werden. Es stellt sich aber auch die Frage, ob man Konvertierungsregeln nicht auch ohne Rückgriff auf die Bedeutung der Teilausdrücke formulieren kann.

47. Hat man nur die Ausdrücke (Q (S P)) mit der Verallgemeinerung, dass S und P ‚gleichwertig‘ sein können im Sinne von (Q (A B)) $latex \vdash$ (Q (B A)), dann stellt sich die Frage welche Kriterien man hätte, gäbe es keinen Bedeutungsbezug?

48. Man muss feststellen, dass ohne irgendeinen Bedeutungsbezug die Ausdrücke als solche keinerlei Ansatzpunkt bieten, eine Konvertierung zuzulassen oder sie zu verbieten.

49. Wenn aber Konvertierungsregeln ohne Bedeutung keinen Sinn machen, dann muss man sich fragen, welche Bedeutungsstrukturen man benötigt, dass man solche Konvertierungsregeln sinnvoll einführen kann.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

50. Wenn es also ohne Bezug auf eine Bedeutung nicht geht, stellt sich die Frage, wie eine solche Bedeutungsstruktur aussehen muss, damit solche – oder auch andere – Konvertierungsregeln formuliert werden können.

51. Die weitere Diskussion wird in einem neuen Blogeintrag fortgeführt werden.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7

Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Avicenna, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsraum, Definition, Definition - explitite, Definition - rekursive, Definition - simultane, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Modell, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekthierarchie, Semantik, Struktur, Syntax

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen.

NAMEN, VERBEN/TERME, PRÄPOSITIONEN

2. Nach all den Vorüberlegungen nähert sich Avicenna nun dem eigentlichen Gegenstand der (antiken, auf das Alltagsdenken bezogenen) Logik, nämlich jenen ‚Ausdrücken‘, durch die entscheidende Bedeutungen kommuniziert werden.
3. Er beginnt mit ‚einfachen‘ Ausdrücken.

4. Er nimmt an, dass sich einfache Ausdrücke e aus drei Teilausdrücken zusammen setzen, die er als ‚Name‘, ‚Verb‘ und ‚Präposition‘ klassifiziert.

5. Terminologisch merkt er an, dass der grammatische Begriff ‚Verb‘ von Logikern ‚Term‘ genannt wird.

6. Sowohl der Name als auch das Verb sollen eine ‚vollständige Bedeutung‘ haben, Präpositionen dagegen nicht.

7. Namen unterscheiden sich von Termen dadurch, dass sie sich nicht auf eine ‚zeitliche Abfolge‘ (engl.: ‚temporal sequence‘) beziehen.

8. Verben hingegen – im Unterschied zu Namen – haben sowohl eine ‚Bedeutung‘ wie auch einen ‚zeitlichen Bezug‘ (engl.: ‚temporal significance‘).

9. Grenzfälle sind Namen wie ‚Heute‘ (engl.: ‚day‘) und ‚Gestern‘ (engl.: ‚yesterday). Obwohl sie einen ‚Teil der Zeit‘ (engl.: ‚part of time‘) bezeichnen (engl.: ’signify‘), sind sie doch keine Verben, da bei diesen Namen ihre ‚Bedeutung‘ mit dem ‚zeitlichen Bezug‘ zusammenfällt; bei einem Term wie ‚geschlagen‘ (engl.: ’struck‘) ist die Bedeutung (Vorgang des Schlagens) klar zu unterscheiden von dem Zeitbezug (der Vorgang war in der Vergangenheit).

10. Beispiele: e = <e1,e2,e3,e4,e5> = N:(Ich)Va:(habe)N:(den Zid)Vb:(gesehen); Der einfache Ausdruck e zerfällt in mehrere Ausdrucksteile <e1,e2,e3,e4,e5>, denen sich Bedeutungen zuordnen lassen. e1 = (Ich), bezieht sich auf den aktuellen Sprecher, und wird von daher als Name [N] für ein Objekt gewertet, das dem Namen eine Bedeutung verleiht. <e3, e4> = (den Zid) bezieht sich auf eine Person Zid, und wird auch als Name für ein Objekt gewertet, das dem Namen eine Bedeutung verleiht. e2 und e5 = (habe) … (gesehen) bezieht sich auf einen Vorgang des Sehens, bei der ein Beobachter etwas sieht (Bedeutungsanteil); zusätzlich wird ein zeitlicher Aspekt angedeutet, dass es sich um einen Vorgang in der Vergangenheit handelt. Ausdruck e1 füllt die ‚Rolle‘ des Beobachters und Ausdruck <e3, e4> spielt die Rolle des beobachteten Objekts.

11. Beispiel: e = <e1,e2,e3,e4> = N:(Zid) V:(ist) PRÄP:(im) N:(Haus). Der einfache Ausdruck e zerfällt in mehrere Ausdrucksteile <e1,e2,e3,e4>, denen sich Bedeutungen zuordnen lassen. e1 = N:(Zid) ist ein Ausdruck, der sich auf eine Person Zid bezieht, die dem Ausdruck als Objekt eine Bedeutung verleiht. e2 = V:(ist) ist ein Ausdruck, der sich auf einen Sachverhalt ‚etwas ist an einem Ort‘ bezieht, der dem Ausdruck sowohl eine Bedeutung verleiht wie auch eine davon unabhängige zeitliche Bestimmung, dass es in der Gegenwart ist. e3 = PRÄP:(im) ist ein Ausdruck, der sich auf einen räumlichen Sachverhalt bezieht ‚etwas ist in einem Raumgebiet‘, der dem Ausdruck eine Bedeutung verleiht, ohne expliziten Zeitbezug. e4 = N:(Haus) ist ein Ausdruck, der sich auf einen Ort Haus bezieht, der dem Ausdruck als Objekt eine Bedeutung verleiht. Die Kombination aus <e2, e3> ergibt einen Sachverhalt, der einerseits ein Objekt verlangt, von dem gesagt wird, dass es sich irgendwo befindet, und ein Objekt, das den Ort markiert. Beides ist mit e1 und e4 gegeben.

DISKUSSION

TERMINOLOGIE

12. Zur Terminologie: dass die (antiken) Logiker ‚Verben‘ als ‚Terme‘ bezeichnen sollen ist eine Sache. In diesem Kontext der Ausdrucksanalyse erscheint es mir eher verwirrend, zwei verschiedene Terminologien zu vermischen. Ich behalte im Folgenden die ‚grammatischen‘ Begriffe bei. Später kann man dann alle grammatischen Begriffe in einem mehr formalisierten logischen Kontext ‚übersetzen‘, falls notwendig.

13. Von ‚einfachen‘ Ausdrücken e zu sprechen, wenn die Ausdrücke sich alle aus mehreren Teilausdrücken e = <e1, e2, e3, …> zusammen setzen, kann verwirrend wirken, zumal er in vorausgehenden Abschnitten mit ‚einfachen‘ Ausdrücken tatsächlich solche meinte, die eben nicht zusammen gesetzt sind. Avicenna gibt keine direkte Erklärung für diese geänderte Verwendungsweise seines Begriffs eines ‚einfachen Ausdrucks‘, aber der Kontext legt folgende Interpretation nahe:

SYNTAX UND SEMANTIK

14. Es gibt eine ’syntaktische‘ Einfachheit (im Sinne von ’nicht zusammen gesetzt‘) und es gibt eine ’semantische‘ Einfachheit. Einfache Aussagen in diesem Abschnitt scheinen zu den ’semantisch einfachen‘ Ausdrücken zu gehören, denn syntaktisch sind sie eindeutig nicht einfach, sondern zusammengesetzt.

DER SEMANTISCHE RAUM

15. Damit stellt sich die Frage, wie man den ’semantischen Raum‘ ( den ‚Bedeutungsraum) eines Ausdrucks e (sowohl syntaktisch einfach als auch syntaktisch zusammengesetzt) so charakterisieren kann, dass man eine ‚einfache‘ Bedeutung von einer ’nicht einfachen = komplexen‘ Bedeutung unterscheiden kann.

16. Avicenna selbst hat ja in den vorausgehenden Abschnitten den ‚Bedeutungsraum‘ nicht ausdrücklich als eigenständigen Gegenstand thematisiert, immer nur indirekt, anhand von einzelnen Beispielen. Von diesen seinen indirekten, fragmentarischen Andeutungen aus lässt sich die Frage nach einer klaren Unterscheidung einer ‚einfachen‘ und einer ’nicht einfachen‘ Bedeutung im Kontext eines Ausdrucks e kaum einfach beantworten.

17. Als ‚Abfallprodukt‘ der bisherigen Rekonstruktion wurde das Konzept einer ‚dynamischen Objekthierarchie‘ O angedeutet, für die allgemeine Metaklassifikationen (entspricht in etwa dem klassischen Kategorienbegriff) wie z.B. ‚echtes Objekt‘ (etwa die Kategorie ‚Substanz‘), ‚unechte Objekte (etwa die Kategorie ‚Qualität‘), ‚Zeit‘, ‚Raum‘ und ‚Zahl‘ (etwa die Kategorie ‚Quantität‘) postuliert werden konnten.

18. Wenn man nun also von einem ‚Bedeutungsraum‘ (semantischen Raum) M sprechen will, dann müsste man entweder diese – bislang nur angedeuteten – Objektstrukturen mit den zusätzlichen Metaklassifikationen zugrunde legen oder eine Alternative formulieren. Ohne irgendwelche Annahmen dieser Art wäre der Begriff des semantischen Raumes vollständig leer und damit jegliche Art von Rekonstruktion von Ausdrücken e mit Bezug auf die zugehörigen ‚Bedeutungen‘ beliebig: alles wäre richtig und zugleich falsch.

19. Bis auf weiteres wird hier die bisherige Skizze zum dynamischen Objektraum mit den Metaklassifikationen als Arbeitshypothese für die weitere Interpretationen benutzt.

20. Von einem Ausdruck e mit Teilausdrücken <e1, e2, e3, …> zu sagen, dass bestimmte Ausdrucksteile $latex e_{i}$ bestimmte, voneinander abgrenzbare Bedeutungen haben, ihnen also unterschiedliche ’semantische Funktionen‘ zukommen, ist einerseits gewagt, da die Ausrücke als solche keinerlei syntaktische Hinweise haben müssen, aus denen man dies erkennen könnte, zugleich aber auch interessant, da damit die Denkaufgabe gestellt wird, wie es möglich sein soll, beliebige Ausdrucksteile $latex e_{i}$ in einem Ausdruck e durch Bezugnahme auf ‚etwas anderes‘, nämlich auf die ‚Bedeutung‘ indirekt charakterisieren zu können.

SIMULTANE DEFINITONEN

21. In gewissem Sinne könnte man hier auch von einem Definitionsvorgang sprechen: das Neue, das Unbekannte, das sind die Ausdruckselemente <e1, e2, e3, …> in einem Ausdruck e, das Bekannte das ist ein vorausgesetztes Bedeutungsgefüge, und die definitorische Erklärung ist die Verbindung von neuem Ausdruckselement und bekanntem Bedeutungsobjekt. Abweichend vom einfache Fall der expliziten syntaktischen Definition von einem Element e durch eine Folge von anderen Ausdrücken <e1, e2, e3, …> haben wir es hier im Falle der Definition von syntaktischen Ausdrücken durch Bezugnahme auf semantische Objekte mit zwei zusätzlichen Aspekten zu tun: (i) die Erklärung findet nicht in ein und demselben syntaktischen Raum statt sondern es werden zwei ansonsten getrennte Räume miteinander verknüpft: der syntaktische Raum mit dem semantischen Raum, und umgekehrt. Ferner (ii) wird nicht nur ein einziges syntaktisches Element ‚erklärt‘, sondern es werden mehrere syntaktische Elemente ‚parallel’/ ’simultan‘ erklärt.

22. Einen vergleichbaren Fall von ’simultaner‘ Erklärung haben wir im Falle von mathematischen Strukturtheorien, wie sie auch bei modernen empirischen Theorien auftreten. Ein typischer Fall wäre eine Struktur wie $latex < M, f1, …, fk >$. Hier werden mehrere Ausruckselemente eingeführt, deren Bedeutung sich erst im (syntaktischen) Gesamtkontext ergibt, der zusätzlich mit semantischen Elementen aufgeladen werden kann.

23. Ein anderes Beispiel sind formale Semantiktheorien, in denen zusammengesetzte Ausdrücke der Art e = <e1, e2, …> durch eine komplexe Abbildungsvorschrift so auf eine formale Struktur (auch ‚Domäne‘ oder ‚Modell‘ genannt) bezogen werden, dass für jeden syntaktisch zusammengesetzten Ausdruck e gesagt werden kann, wann das ‚Modell‘ M diese syntaktischen Ausdrücke ‚erfüllt‘, oft geschrieben $latex M \models e$ mit ‚e‘ als dem Ausdruck, der durch das Modell ‚erfüllt‘ wird.

24. Eine Besonderheit bei diesen Charakterisierungen von Ausdruckselementen e über den ‚Umweg‘ einer Bedeutungsstruktur M liegt darin, dass es nicht ausreicht, jedem einzelnen Teilausdruck $latex e_{i}$ eine – quasi isolierte – Bedeutung zuzuordnen, sondern die einzelnen bedeutungsfundierenden Objekte O der Bedeutungsstruktur M kommen in bedeutungsspezifischen Anordnungen (in Raum, Zeit, …) vor. Diese spezifischen Sachverhalte müssen in den Ausdruckselementen mitkodiert werden. Es reicht also nicht, nur zu sagen, dass das Ausdruckselement ‚e1‘ ein Objekt o1 bezeichnet, das für eine konkrete Person steht, sondern man muss zusätzlich auch – meistens – einen möglichen ‚Vorgang‘ benennen, in den das Objekt o1 eingebettet ist, und – meistens – zusätzlich mit einem zeitlichen Aspekt. Das wären dann schon mindestens drei verschiedene Kodierungsdimensionen, die im Bereich der Ausdruckselemente repräsentiert werden müssten.

25. Aufgrund der Beispiele von Avicenna gäbe es die zusätzlichen Arbeitshypothesen, dass (i) Vorgänge durch ‚Verben‘ [V] kodiert werden, (ii) zeitliche Aspekte sowohl durch Verben wie auch durch ‚Namen‘ [N], und (iii) räumliche Aspekte durch ‚Präpositionen‘ [PRÄP].

26. Die interessante Frage wäre natürlich, wie genau diese verschiedenen Objektstrukturen und -eigenschaften und -Relationen in der dynamischen Objekthierarchie O als dem Bedeutungsraum M repräsentiert sind. Sie müssten ja so vorliegen, dass man sie einfach ‚ablesen‘ könnte und dann durch einen entsprechenden ‚Übersetzungsprozeß‘ von M nach E zugeordnet werden könnten, also $latex \lambda: M \longrightarrow E$ (mit $latex \lambda $ als Übersetzungsvorschrift).

27. Nehmen wir das Beispiel e = <e1,e2,e3,e4> = N:(Zid) V:(ist) PRÄP:(im) N:(Haus). Es gibt hier (woher wissen wir dies überhaupt!) zwei Ausdruckselemente e1 und e4, die sich auf ‚echte Objekte‘ beziehen; e1 bezieht sich auf eine konkrete Personen, e4 auf ein Objekt, in dem Menschen sich aufhalten können. Der Ausdruck ist kein echtes Objekt, da es nur eine bestimmte Form von Beziehung zwischen zwei Objekten repräsentiert, nämlich dass ein Objekt A ‚räumlich in‘ einem anderen Objekt B vorkommt. Das Ausdruckselement e2 repräsentiert einen Zusammenhang zwischen zwei Objekten (echt oder unecht), der zudem aktuell ist, genauer: von einem Zielobjekt A wird gesagt, dass es in einer ist-Beziehung zu einem anderen Objekt steht. Da aber nach dem ‚Sprachgefühl‘ (was ist das?) die Kombination <e1, e2, e4> nicht geht, muss also <e3,e4> zusammen auftreten, damit e1 mittels e2 mit e4 kombiniert werden kann. Eine Arbeitshypothese könnte sein, dass echte Objekte, die mögliche ‚Orte des Vorkommens‘ bezeichnen, eine zusätzliche Präposition benötigen, um als Gegenpart in einer ist-Relation auf zu treten. Das ist natürlich hier alles sehr ad hoc und unsystematisch. Es kann aber verdeutlichen, dass die große Arbeitshypothese mit der bereichsübergreifenden Zuordnung $latex \lambda $ von Elementen einer Bedeutungsstruktur M (mit der dynamischen Objekthierarchie O als Teilstruktur) zu einer Menge E von möglichen Ausdrücken eine sehr detaillierte Beschreibung verlangt, die nicht ad hoc entscheidet, sondern systematisch.

Eine Fortsetzung zu diesem Beitrag findet sich HIER.

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

PHILOSOPHIE – ÜBER SICH NACHDENKEN – PROGRAMMIEREN – DIE KALTE MASCHINE – DER GEIST IM STROMKREIS

Kode, kodieren, Kodierung, Kognitives Interface, Mentales Modell, Programm, Programmiersprache, Programmiersprache - visuelle, Semantik, Software, Softwareengineering, Sprachspiel, Wittgenstein

Letzte Änderung: 29.Mai 2014, 19:20h (Musikstück hinzugefügt)

SOUNDEREIGNIS

Zur Einstimmung der folgenden Reflexionen über das Programmieren aus philosophischer Sicht hier eine Sound-Komposition vollständig erstellt mit mathematischen Algorithmen: Sinfonia made completely by MAX Demos. Das Stück besteht aus 6 Klangspuren, wobei jede Spur einen Klang repräsentiert, der durch Softwareinstrumente erzeugt worden ist. Für alle die, die nur ‚Mainstream-Musik‘ kennen (Klassik gehört auch zum ‚Mainstream :-)) ist vom Hören abzuraten. Dies ist ein Sound für jene, die sich vom Mainstream gelöst haben und einfach Spass haben, unbekannte Klangräume zu durchwandern. Konkret habe ich mit Demoinstrumenten aus den Tutorials der Software MAX 6.1.7 sowie ableton live 9.1 und Max4Live herumgespielt.

ZWEI JUNGE MÄNNER TRETEN AUF

1. Am 22.Mai 2014 abends, nach einem sehr anstrengenden Tag, war ich Zeuge eines besonderen Schauspiels. Zwei junge Männer, beide langjährige Programmierer im Kontext innovativer multimedialer Anwendungen, Erfinder einer dafür eigens geschaffenen Programmiersprache – nennen wir sie Lx – dachten in zwei aufeinanderfolgenden Vorträgen laut nach, über das, was sie tun, wenn sie programmieren.

2. Dies ist ungewöhnlich, da diejenigen, die programmieren, es normalerweise einfach tun; sie schreiben ‚Kode‘, wie es so schön heißt. Verschachteln if’s und ‚while’s‘ und zahllose Schlüsselwörter der vielen ‚Bibliotheken‘ der fertigen Softwaremodulen, die heutzutage Programmiersprachen begleiten.

3. In der ‚reinen Lehre‘ ist s zwar anders, da gibt es Entwurfsmodelle, abstrakte Spezifikationen, seitenlange Anforderungen, die einem Programmierer sagen sollen, was er ‚eigentlich‘ zu tun hat; doch aus der Sicht eines Programmierers verschwimmen diese ganzen Texte und Diagramme sehr schnell zu einem Nezwerk von Kodierungsanweisungen, zu Seiten voller kryptischer Befehlsausdrücken, zu einem Programmtext seiner Sprache Lx. Was immer abstrakt vorher gedacht worden ist, er, der Programmierer verwandelt sich in einen ‚Kodierer‘.

4. Nicht so an diesem Abend. Die beiden Programmierer versuchten über ihr Kodieren nachzudenken.

ZUR GESCHICHTE DER KODIERUNG

5. Im ersten Vortrag ging es mehr um die historische Dimension, wie es von ersten rechnenden Maschinen (mit schönen Videoausschnitten über Konrad Zuse und seinen pionierhaften Experimenten mit seinen ersten Rechnern) mit direkter bitweiser Kodierung zu immer abstrakteren Programmiersprachen (Bits, Hexcode, mnemonischer Assemblercode, einfache Programmiersprachen wie Fortran und C, höhere objektorientierte Sprachen, und dann visuelle Kodierung). Da endete der historische Aufriss, da die Sprache Lx der beiden Programmierer solch eine visuelle Sprache war.

6. An dieser Stelle ruckelte es schon ein bisschen. Erstens gibt es ja heute schon viele verschiedene visuelle Programmiersprachen, und zum anderen war der Überblick unvollständig. Die Programmiersprachen selbst sind nur ein Teil der Geschichte; parallel mit den Programmiersprachen hat sich unter dem Oberthema ‚Softwareengineering‘ ein Denkmuster entwickelte, das die Programmiersprache nur noch als ein – wenngleich ein wichtiges – Moment sieht im Kontext von – stark vereinfachend – Problemstellung P, Anforderungsanalyse A, logisches Entwurfsmodell M und implementiertes System S. Kodierung ist Teil des implementierten Systems S bzw. steht in gewisser Beziehung zum logischen Entwurfsmodell. Der ‚Denkraum‘ des Softwareeinsatzes hat sich also erheblich ausgeweitet, und eine Geschichte der Programmierung, die diesen Denkkontext des Programmierens nicht berücksichtigt, wirkt mindestens unvollständig.

DIAGRAMMATISCHE REFLEXE ZTUM EIGENEN KODIEREN

7. Der zweite Vortrag wurde in gewisser Weise ‚persönliches‘ bis ’sehr persönlich‘. Hier sprach der Programmierende – nennen wir ihn B – in der Tat über seine Gedanken, wenn er programmiert bzw. über seine Gedankenwelt, vorher, während und nachher, und er sprach als jemand, der eine Programmiersprache entwickelt hat, sie benutzt, sie ‚warten‘ muss und sie weiter entwickelt.

8. Er benutze dazu Folien die angefüllt waren mit Handzeichnungen, Wortskizzen, Wort und Bildskizzen – fantastisch anzuschauen, eher Kunstwerken gleich, anregend, faszinierend. Seine begleitende Rede war auch keine normale Rede, keine geschliffenen Sätze, kein zusammenhängender Text; nein, es war eine Mischung aus Stammeln, Brummeln, meist mit dem Rücken zu den Zuhörer, eine Art Zwiegespräch mit den kunstvollen Linien in dem projizierten Bild; meist kryptisch, die Zuhörer/ Zuschauer meist in Lauerstellung in Erwartung, was denn jetzt kommen würde.

9. Es klingt komisch, aber ich habe es genossen, das war Denken unplugged, das war Kreativität des sich selbst reflektierenden Kodierens ‚live‘. Es dürfte nicht allzu viele ‚Programmierer‘ geben, die dies so tun würden. Als ich den Vortragenden anschließend darauf hin ansprach, wie oft er das so schon gemacht habe, sagte er auch, dass er dies so zum ersten Mal gemacht habe. Also eine Uraufführung; wunderbar.

PHILOSOPHISCHE REFLEXION

10. Schaltet man jetzt die philosophische Reflexion ein, dann ist als erstes zu bemerken, dass es offensichtlich nicht ganz selbstverständlich, keinesfalls einfach ist, etwas, was man tut, – hier das Programmieren, das Kodieren in einer Sprache Lx – in einer anderen Sprache Lxx auszudrücken. So beeindruckend und faszinierend die bildhaften und textuellen Fragmente waren, die B in seinen Folien präsentierte (für mich wahre ‚Kunstwerke‘), so wenig ließen diese vielen Fragmente einen größeren Zusammenhang klar erkennen. Dieser Eindruck verstärkte sich auch in dem anschließenden Gespräch mit den Zuhörern. Während die meisten ‚Anwender‘ waren, die die Sprache Lx (bzw. der Vorläuferversion) selbst zum Kodieren benutzten, und der Vortragende B aber gedanklich im Netzwerk seiner Konzepte ?herumirrte?, gab es auch Fragen zum ‚Denkraum‘, innerhalb dessen man Programmiersprachen entwickelt. Fragen und Antworten fanden nicht wo wirklich zueinander.

11. Während im ersten Vortrag noch ein wenig die Idee anklang, dass das Aufkommen von visuellen Sprachen eine ‚Verbesserung‘ für den programmierenden Menschen darstellt, blieb dieser reformerische, am Menschen orientierte, Ansatz immer mehr im Dunkeln. Im Zweikampf mit seinen eigenen Gedanken wurde nicht klar, ob und wie denn eine visuelle Programmiersprache Lx (zu der es, wie gesagt, viele Parallelen gibt) dem ‚menschlichen Denken‘ besonders entgegen kommt.

12. Während die Missionare des objektorientierten Programmierens zumindest versucht haben, Formen des alltäglichen Denkens mit einer ojektorientierten Sprache Lo in Verbindung zu bringen (was beim späteren sogenannten ‚modellbasierten‘ Programmieren schon nicht mehr so gelang), wurden solche Gedanken an diesem Abend nicht vorgetragen. Der Mensch in seinem Denken – hier der programmierende Mensch – blieb weitgehend außen vor. Schade. In diesem den Menschen und vorhandenen Programmieralternativen ausklammernden Denken blieben die Gedanken des suchenden Programmierers weitgehend ‚alleine mit sich selbst‘.

SOFTWAREENGINEERING IST NICHT GANZ NEU

13. Bemerkenswert an diesem Schauspiel ist die Tatsache, dass Software engineering (nicht ganz so gut: Softwaretechnik) nun ja keine wirklich ganz neue Disziplin mehr ist. An allen Universitäten/ Hochschulen, in denen Informatik gelehrt wird, gibt es seit mindestens 20 Jahren auch Softwareengineering. Und dennoch ist diese Art eines ‚zusammenhängenden Denkens‘ in den Köpfen der ‚aktiven Programmierenden‘ offensichtlich nicht präsent (als Vergleich: die Ideen eines Galilei haben ca. 100 Jahre gebraucht, bis sie zum Allgemeingut geworden sind).

14. Dennoch kamen man auch bei jenen, die Softwareengineering im größeren Zusammenhang denken, wissenschaftstheoretische bzw. philosophische Ansätze kaum bis gar nicht vorkommen, obgleich ein solches Denken hier eine Menge zu tun hätte.

15. Halten wir kurz fest: der Aspekt des menschlichen Denkens – nennen wir es hier das ‚kognitive Interface‘, die ‚Schnittstelle zum Denken‘; andere sprechen auch von ‚mentalen Modellen‘ – kam bei den beiden Vortragenden des Abends so gut wie nicht vor.

16. Der Einsatz einer Programmiersprache hat aber noch eine weitere Dimension, die nicht minder bedeutsam ist. Egal welche Programmiersprache Lx man benutzt, ein Programm in solch einer Sprache Lx – nennen wir es P(Lx) – muss irgendwann von einem realen Computer C ‚ausgeführt‘ werden. Dies bedeutet, was immer sich ein menschlicher Programmierer im Rahmen seines kognitiven Interfaces ‚gedacht‘ haben mag, als er P(Lx) erstellt hat, das, was ‚tatsächlich passiert‘, das entscheidet sich bei der realen Ausführung auf einem Computer C. Dies bedeutet, dass die Menge dieser Ausführungen von P(Lx) auf dem Computer C – nennen wir sie C(P(Lx)) – die ‚finale Bedeutung‘ von Lx darstellt. Man spricht auch von der ‚Semantik‘ (Bedeutung) der Sprache Lx mit Bezug auf C. Beispiel: mit den Ausdrücken von Lx will Programmierer B zwei ‚parallele Prozesse‘ a und b darstellen, gefolgt von Prozess c. Damit dieser Gedanke Sinn macht, muss sichergestellt sein, dass bei der Ausführung von a,b und dann c diese logische Struktur auch real umgesetzt wird, erst recht, wenn möglicherweise das Ergebnis von c z.B. dann wieder dem Prozess b als ein Teil seiner Eingangswerte zur Verfügung gestellt werden soll. Solche ‚Korrespondenzen‘ zwischen ‚intendierter‘ Bedeutung und ‚realisierter‘ Bedeutung herzustellen und zu ‚gewährleisten‘ ist generell nicht einfach und in genügend vielen Fällen unmöglich. Über diese ’semantischen Aspekte‘ der Programmiersprache Lx wurde gar nicht gesprochen. Auf Nachfrage kam eine Aussage, die so klang, also ob man darüber ’noch nicht nachgedacht habe‘.

17. Mir kommt es so vor, als ob das Thema ‚Semantik einer Programmiersprache‘ für viele Programmierenden das ist, was Tiefenpsychologen das ‚individuelle Unbewusste‘ nennen. Irgendwo wissen sie zwar, dass ihr Kode letztlich von einer Maschine abgearbeitet wird mit den daraus resultierenden Einschränkungen, aber tatsächlich berauschen sie sich lieber an ihren aktuellen Ideen und Fantasien und tun so, als ob das alles ja genau so auch umgesetzt wird. Wird es nicht. Hier gibt es viele zu klärende Fragen, also philosophisches Potential.

WITTGENSTEIN LÄSST GRÜSSEN

18. Vielen Programmierenden – den meisten? – ist nicht bewusst, dass der Denkweg von Ludwig Wittgenstein von seinem ‚Tractatus Logico Philosophicus‘ hin zu seinen ‚Philosophischen Untersuchungen‘ ein wunderbares Muster abgibt, innerhalb dessen man auch die Thematik der Bedeutung von Programmiersprachen reflektieren kann. Natürlich müsste man die Diktionen von Wittgenstein dem heutigen Sprach- und Denkgebrauch des Softwareengineerings etwas anpassen, aber die Grundideen (und die sich darin verbergenden kritischen Potentiale) sind weiterhin anwendbar.

19. Eine zentrale Idee Wittgensteins ist die Aufdeckung der Tatsache, dass die Ausdrücke einer Sprache L – und das gilt dann auch für Lx – ihre ‚Bedeutung‘ nur im Kontext sogenannter ‚Sprachspiele‘ haben. Im Fall der visuellen Programmiersprache Lx wäre ein solcher Kontext gegeben durch (i) die Programmierer, (ii) die Ausdrücke von Lx, (iii) die ausführenden Computer C (meistens mindestens mit Hardware und Betriebssystem) sowie (iv) die ‚Aktionen‘, die der programmierte Computer – z.B. als Roboter oder als Smartphone – beobachtbar ‚ausführt‘, sehr oft in ‚Interaktion mit einem (v) Benutzer‘, der ’seine‘ ‚Vorstellungen‘ (:= mentale Modelle) des Geschehens hat.

20. Das Softwareengineering versucht – im idealen Fall – die potentiellen Sprachspiele ‚vorweg‘ zu analysieren, zu modellieren, und entsprechend zu implementieren. Die Grenzen liegen bei der ‚Vorwegnahme‘ des potentiellen Benutzers.

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.