(Letzte Änderung 25.Sept.2014, 09:20h)
Die ‚innere Seele‘ der Formen korrespondiert immer mit Klängen. Hier ein weiteres Klangexperiment…… der Klangraum ist unendlich groß …
VORGESCHICHTE
Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.
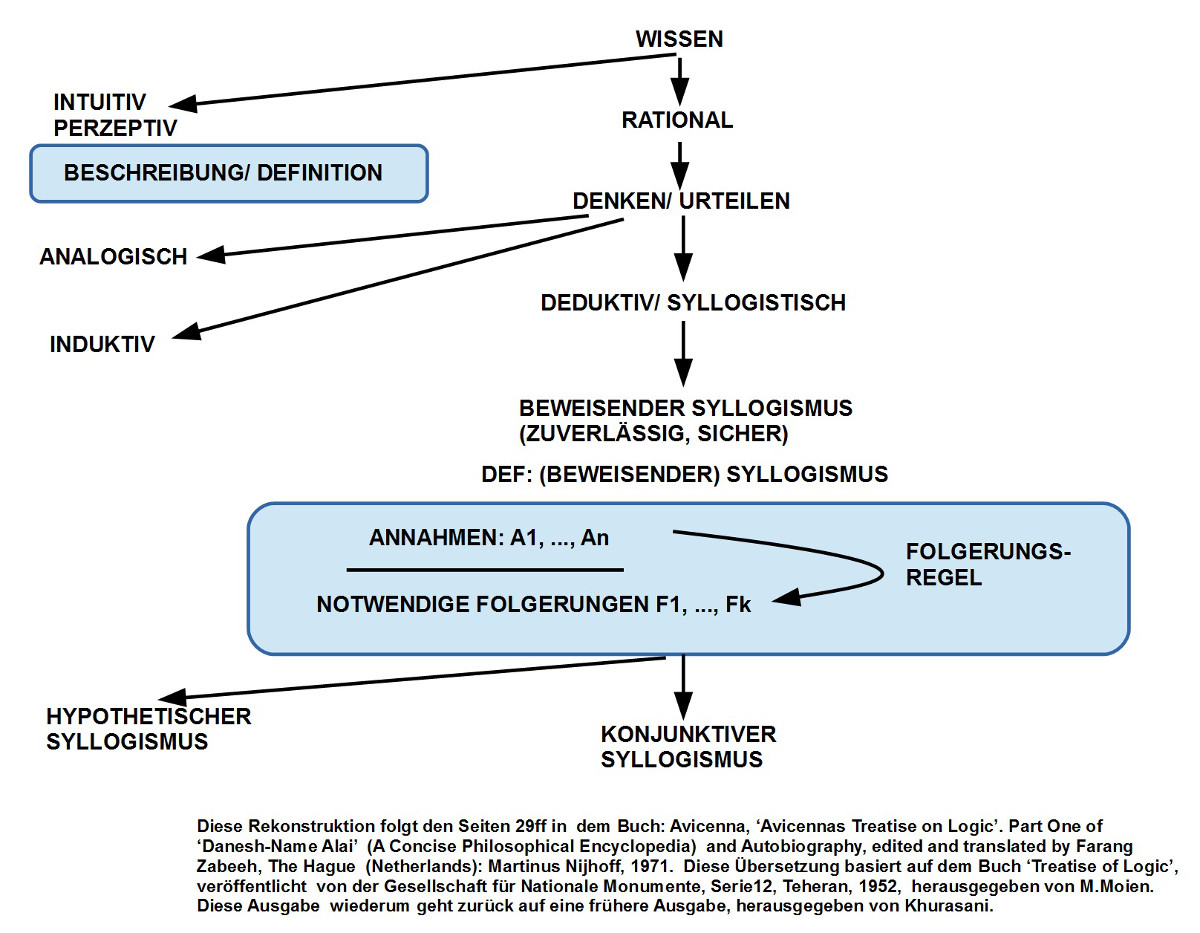
1. Nach den vorausgehenden Detailbetrachtungen weitet sich nun der Blick Avicennas auf das Wissen allgemein, und konzentriert sich im Wissen auf das schlussfolgernde Denken in Form von ‚beweisenden Syllogismen‘ (engl.: ‚demonstrative syllogisms‘). Laut Anmerkung des Übersetzers folgt er hier – wie auch in den meisten Teilen zuvor – weitgehend Aristoteles.
2. Avicenna definiert einen (beweisenden) Syllogismus durch die Komponenten (i) Jene Aussagen A1, …, An, die zum Zeitpunkt des Argumentierens als ‚wahr‘ angenommen werden, (ii) Folgerungsregeln, mittels deren man von gegebenen wahren Aussagen auf andere wahre Aussagen ‚mit Notwendigkeit folgern‘ kann, sowie (iii) jene Aussagen F1, …, Fk, die mittels solcher Folgerungsregeln aus den gemachten ‚Annahmen‘ ‚mit Notwendigkeit‘ gefolgert worden sind.
3. [Anmerkung: in einer modernen Schreibweise könnte man einen Syllogismus auch hinschreiben als $latex \{A1, …, An\} \vdash \{F1, …, Fk \}$ gelesen: die Aussagen F1, …, Fk folgen aus den Annahmen A1, …, An mit Hilfe des Folgerungsbegriffs $latex \vdash$ mit Notwendigkeit.]
4. Er unterscheidet dann zwei Arten von Syllogismen: (i) ‚Konjunktive‘ Syllogismen und (ii) ‚Disjunktive‘.
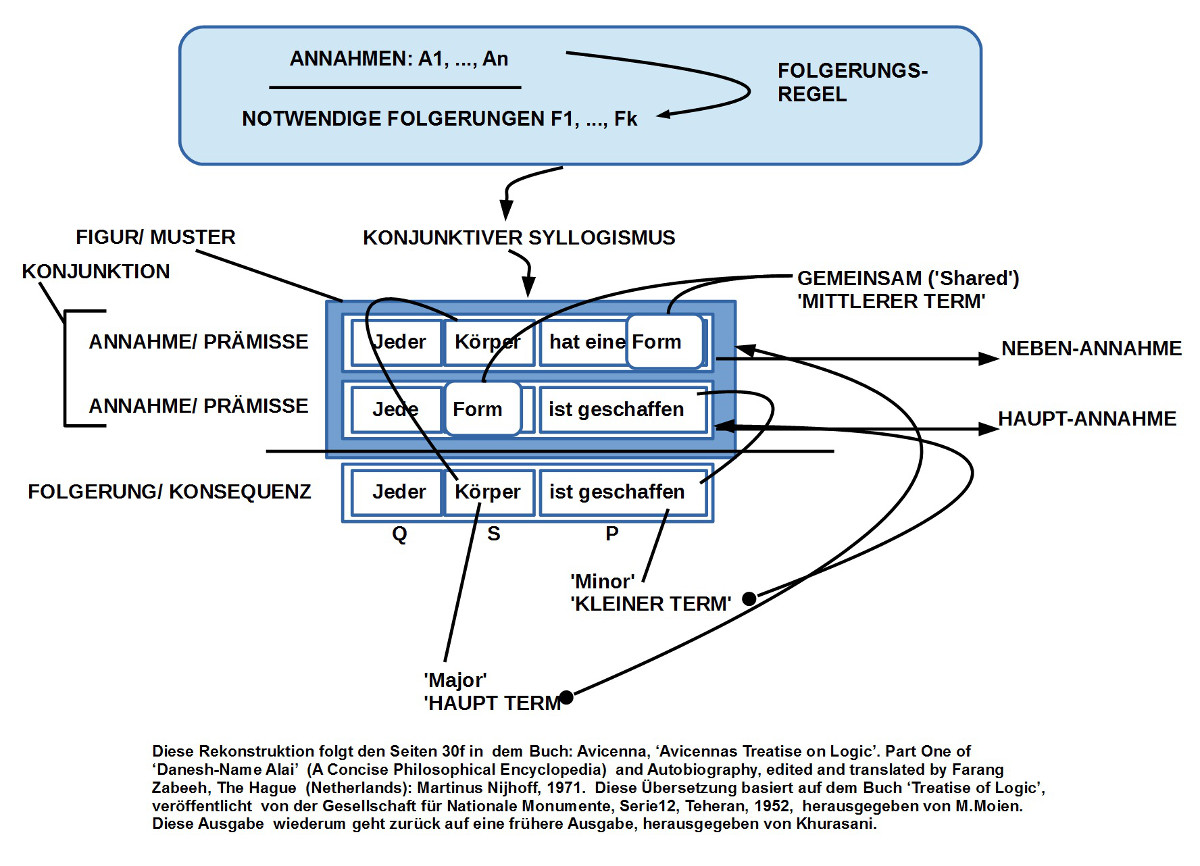
5. Mit der Vorstellung des ‚Konjunktiven Syllogismus‘ führt Avicenna dann – auch hier Aristoteles folgend – eine Reihe von technischen Begriffen ein, um ‚über‘ Syllogismen sprechen zu können.
6. (Konjuktive) Syllogismen bestehen aus drei ‚Aussagen‘, von denen die ersten beiden die ‚Annahmen‘ (‚Prämissen‘) sind, und die dritte die ‚Folgerung‘ (‚Konsequenz‘) aus den vorausgehenden Annahmen.
7. Annahmen wie Folgerungen bestehen jeweils aus drei ‚Ausdrucksteilen‘ A = (A1 A2 A3), von denen er die Ausdrucksteile ‚A2‘ und ‚A3‘ ‚Terme‘ nennt. Der Ausdrucksteil ‚A1‘, bekommt keine eigene Benennung, repräsentiert aber den ‚Quantor‘. Terme können ‚Subjekte S‘ oder ‚Prädikate P‘ sein.
8. Diejenigen Terme in den beiden Annahmen, die in beiden Annahmen gemeinsam sind, nennt er ‚Mittlere Terme‘. Entsprechend nennen wir die beiden anderen, komplementären, Terme hier ‚äußere Terme‘. Den Term in in einer Folgerung, der das Subjekt S repräsentiert und der kein mittlerer Term in einer Annahme ist, nennt er ‚Haupt-Term‘ (‚Major‘). Entsprechend nennt er den Term in einer Folgerung, der das Prädikat P repräsentiert und der kein mittlerer Term ist, den ‚kleinen Term‘ (‚Minor‘). Diejenige Annahme, in der der Haupt-Term der Folgerung vorkommt, wird ‚Neben-Annahme‘ genannt; die andere entsprechend ‚Haupt-Annahme‘.
9. Die typische Aussagestruktur in den Annahmen und in der Folgerung sieht dann so aus: Q (S P). Dabei ist zu beachten, dass Avicenna bei den Syllogismen keine Zeit- und keine Raum-Quantoren benutzt, sondern nur Anzahl-Quantoren, und diese treten nur ‚einfach‘ auf, indem sich der eine Quantor ‚Q‘ in Q(S P) auf die Elemente des Subjekt-Terms S bezieht. Ferner versteht er unter einer ’negativen‘ Aussage nicht die Verneinung der ganzen Aussage – also nicht $latex \neg Q(S\ P)$ –, sondern die Verneinung des Prädikat-Terms P – also $latex Q(S\ \neg P)$ –.
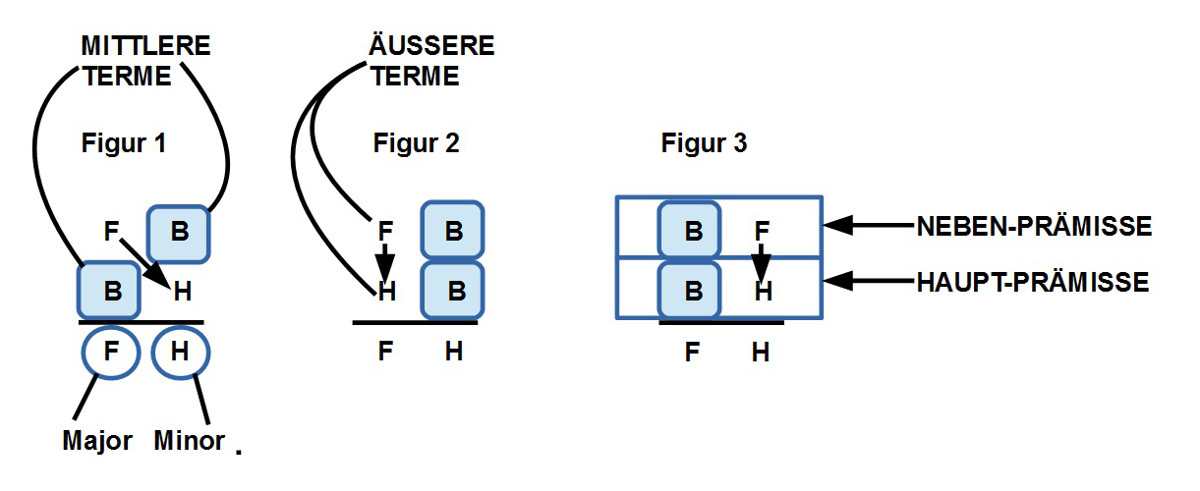
10. Avicenna stellt dann 3 Muster von Syllogismen vor (siehe Schaubild). Sie sind im wesentlich ’sortiert‘ nach der Verteilung der mittleren bzw. äußeren Terme. Zusätzlich zu den Mustern der mittleren Terme unterscheidet er noch, welche Quantoren die Aussagen haben und ob sie ‚affirmativ‘ oder ’negativ‘ sind.
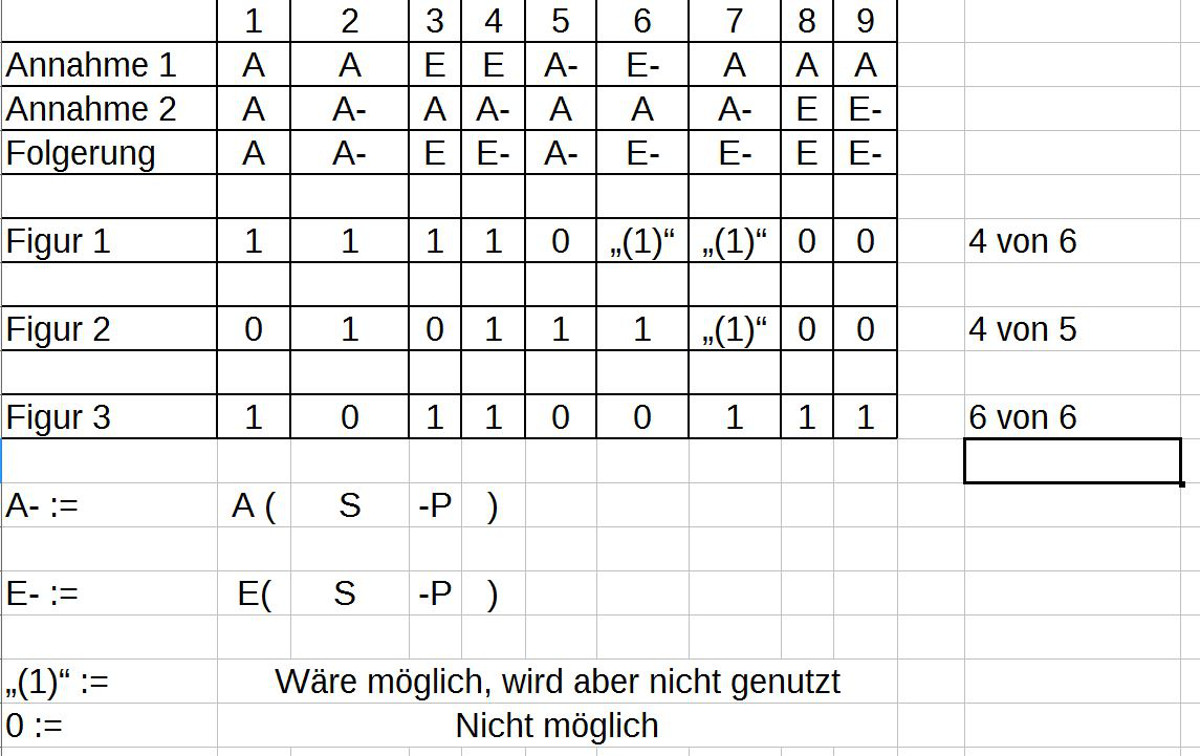
11. Die Tabelle zeigt, welche Quantorenkombinationen Avicenna insgesamt berücksichtigt hat, wie er diese auf die einzelnen Schlußfiguren aufgeteilt hat, und wie ‚asymmetrisch‘ die Verteilung auf die einzelnen Schlußfiguren ausfiel. Auffällig ist, dass Avicenna nicht alle Quantorenkombinationen brücksichtigt, die möglich wären.
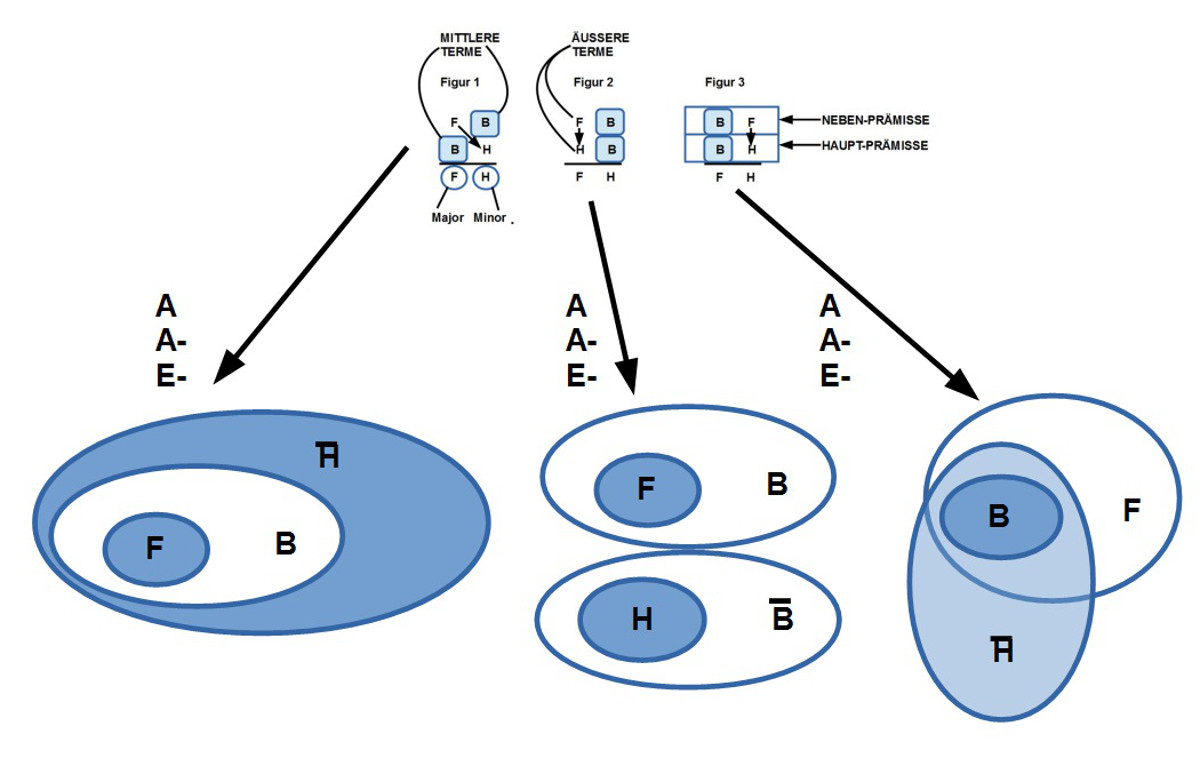
12. Am Beispiel der Quantorenkombination (A, A-)E- zeigt das vorausgehende Schaubild, wie unterschiedlich diese Kombination entsprechend den drei Figuren interpretiert wird. Auffällig ist, dass zwei der möglichen Kombinationen für die Schlussfiguren 1 und 2 von Avicenna nicht genutzt werden.
Fortsetzung folgt
QUELLEN
- Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
- Digital Averroes Research Environment
- Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
- Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
- Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
- Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
- Stanford Encyclopedia of Philosophy, Aristotle’s Logic
- Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7
Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER